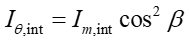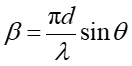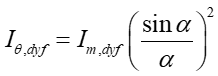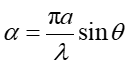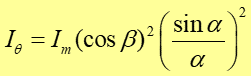Natężenie światła w obrazie dyfrakcyjnym30.4 Interferencja i dyfrakcja na dwóch szczelinach
W doświadczeniu Younga przyjmowaliśmy, że szczeliny są punktowe tj. a << λ. W wyniku interferencji fal spójnych ugiętych na takich szczelinach otrzymywaliśmy prążki interferencyjne o jednakowym natężeniu. Dla realnych szczelin trudno jest zrealizować warunek a << λ. Oznacza to, że pojedyncza szczelina będzie dawała obraz dyfrakcyjny i w wyniku interferencji fal z dwóch szczelin otrzymamy obraz, w którym natężenia prążków nie będą stałe (jak w doświadczeniu Younga) ale zależne od tego obrazu dyfrakcyjnego.
Przypomnijmy, że natężenie światła w obrazie interferencyjnym dla dwóch punktowych szczelin dane jest wyrażeniem
|
(30.14) |
|
(30.15) |
gdzie d jest odległością między szczelinami.
Natomiast natężenie fali ugiętej na szczelinie jest dane równaniem
|
(30.16) |
|
(30.17) |
gdzie a jest szerokością szczeliny.
Teraz chcemy otrzymać łączny efekt. Dlatego w równaniu (30.14) stałą amplitudę obrazu interferencyjnego (dla wąskich szczelin) zastępujemy realnym natężeniem dyfrakcyjnym (30.16). Otrzymujemy
|
(30.18) |
Ten wynik opisuje następujące fakty. W danym punkcie na ekranie natężenie światła, z każdej szczeliny osobno, jest dane przez obraz dyfrakcyjny tej szczeliny. Obrazy dyfrakcyjne dwóch szczelin rozpatrywanych oddzielnie nakładają się, fale interferują.
Na rysunku 30.5 pokazany jest ten wynik dla d = 50λ i trzech wartości stosunku a/λ. Widzimy, że im szersze szczeliny tym wpływ dyfrakcji jest silniejszy (natężenia prążków są bardziej zmienione). Uzyskany obraz jest zgodnie z równaniem (30.18) iloczynem czynnika interferencyjnego i dyfrakcyjnego.
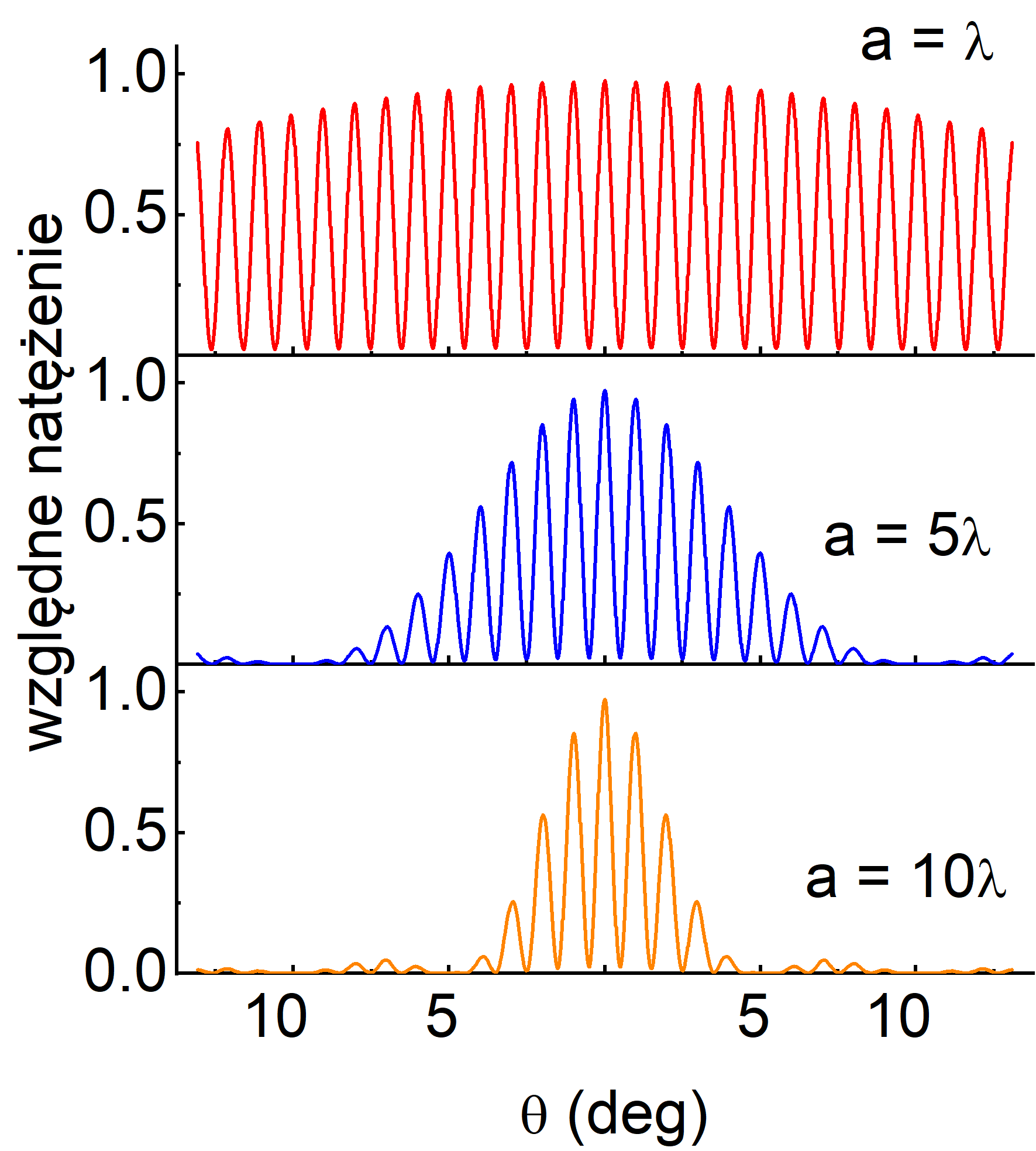
Rys. 30.5. Prążki interferencyjne dla dwóch szczelin o skończonej szerokości
To nakładanie się czynnika interferencyjnego i dyfrakcyjnego jest jeszcze lepiej widoczne na rysunku 30.6. Czynnik interferencyjny ~cos2β jest pokazany na górnym wykresie, czynnik dyfrakcyjny ~(sinα/α)2 na środkowym, a ich iloczyn na dolnym. Widzimy, że obwiednie prążków interferencyjnych pokrywają się dokładnie z obrazem dyfrakcyjnym.
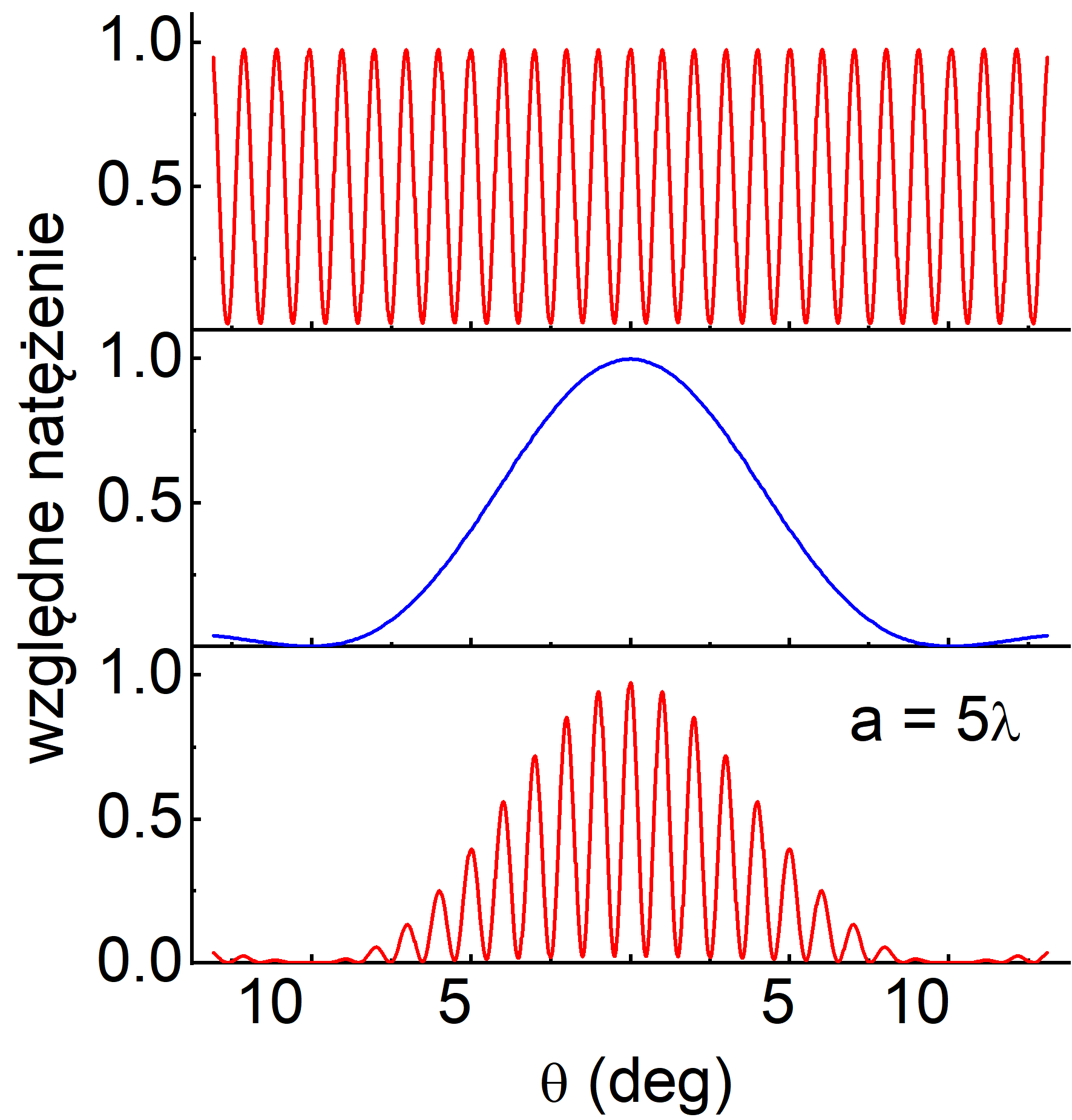
Rys. 30.6. Obraz interferencyjny dwóch punktowych szczelin, obraz dyfrakcyjny pojedynczej szczeliny i ich iloczyn
|
Symulacje komputerowe Możesz prześledzić wynik interferencji dla dwóch szczelin o skończonej szerokości korzystając z programu komputerowego "Dyfrakcja2", dostępnego na stronie WWW autora i na stronie Open AGH. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera. |
