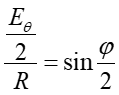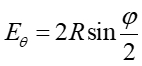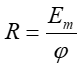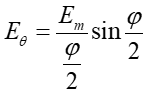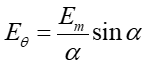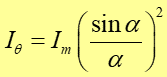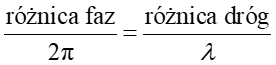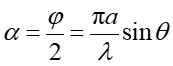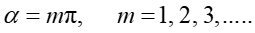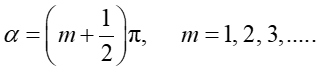30. Dyfrakcja
• Spis treści  
• Interferencja i dyfrakcja na dwóch szczelinach  
•   Dyfrakcja na pojedynczej szczelinie

30.3 Natężenie światła w obrazie dyfrakcyjnym

  Chcemy teraz znaleźć wyrażenie na rozkład natężenia w całym ekranie w funkcji kąta θ. Szczelinę dzielimy na N odcinków i każdy z nich traktujemy jak źródło zaburzenia falowego. Zakładamy, że dla małych kątów θ zaburzenia falowe docierające do punktu P z różnych miejsc szczeliny mają jednakowe amplitudy E₀. Wtedy w punkcie P dodaje się N wektorów natężenia pola elektrycznego E o tej samej amplitudzie E₀ i tej samej częstości. Różnica faz między falami pochodzącymi z sąsiednich odcinków szczeliny wynosi φ. Szukamy zatem zaburzenia wypadkowego dla różnych punktów P, tj. dla różnych kątów θ, co równocześnie odpowiada różnym wartościom φ.

Skorzystamy tu z graficznej metody dodawania amplitud zaburzeń falowych. W tej metodzie każdej fali odpowiada wektor (nazywany wskazem), którego długość reprezentuje amplitudę fali, a kąt względem osi x fazę. Amplitudę wypadkową fali znajdujemy jako sumę wektorów amplitud (wskazów) uwzględniając tym samym amplitudy fal składowych jak i różnice faz między falami.  Więcej o ... . składaniu drgań metodą wektorową.

Na rysunku 30.3 poniżej jest przedstawiona konstrukcja geometryczna, za pomocą której obliczymy natężenie światła w przypadku dyfrakcji na jednej szczelinie.

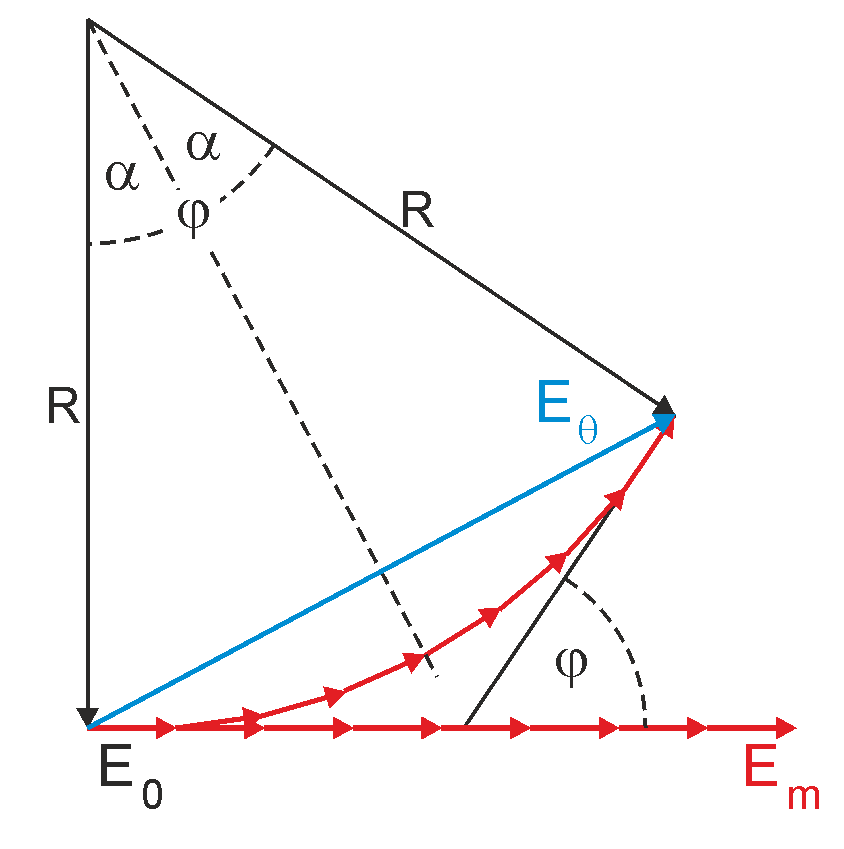
 Rys. 30.3. Graficzne dodawanie wektorów amplitud (wskazów) w przypadku dyfrakcji na jednej szczelinie

Łuk okręgu jest utworzony z wektorów amplitud fal pochodzących z N elementarnych źródeł w szczelinie. Długość łuku wynosi E_m czyli jest równa maksymalnej amplitudzie w środku obrazu dyfrakcyjnego (linia prosta strzałek). Kąt φ w dolnej części rysunku przedstawia różnicę fazy między skrajnymi wektorami w łuku tzn. φ jest różnicą faz pomiędzy promieniami wychodzącymi z góry i dołu szczeliny.

Z rysunku 30.3 widać, że zachodzi związek

W mierze łukowej kąt więc

Podstawiając tę zależność do równania (30.5) otrzymujemy

gdzie α =  φ/2.

Wektory na rysunku 30.3 odpowiadają amplitudom pola elektrycznego. Żeby otrzymać natężenie światła trzeba amplitudy podnieść do kwadratu, więc na podstawie równania (30.8) otrzymujemy

Jak widzimy, w przeciwieństwie do obrazu interferencyjnego, natężenia kolejnych maksimów dyfrakcyjnych nie są jednakowe.

Ponieważ φ jest różnicą faz dla promieni wychodzących z brzegów szczeliny o szerokości a, więc różnica dróg jakie przebywają te promienie do punktu P wynosi asinθ. Korzystając z relacji

otrzymujemy

Łącząc równania (30.9) i (30.11) możemy obliczyć natężenie światła dla obrazu dyfrakcyjnego otrzymanego dla pojedynczej szczeliny. Widzimy, że natężenie I_θ przyjmuje wartości minimalne dla

Podstawiając tę zależność do równania (30.11) otrzymujemy wynik zgodny z uzyskaną poprzednio zależnością (30.2).

Podobnie jest z wartościami maksymalnymi natężenia, które otrzymujemy dla

Na rysunku 30.4 poniżej przedstawiono rozkład natężenia światła (krzywe I_θ) w funkcji położenia na ekranie (kąta θ) dla różnych szerokości szczeliny
(w stosunku do długości fali λ).

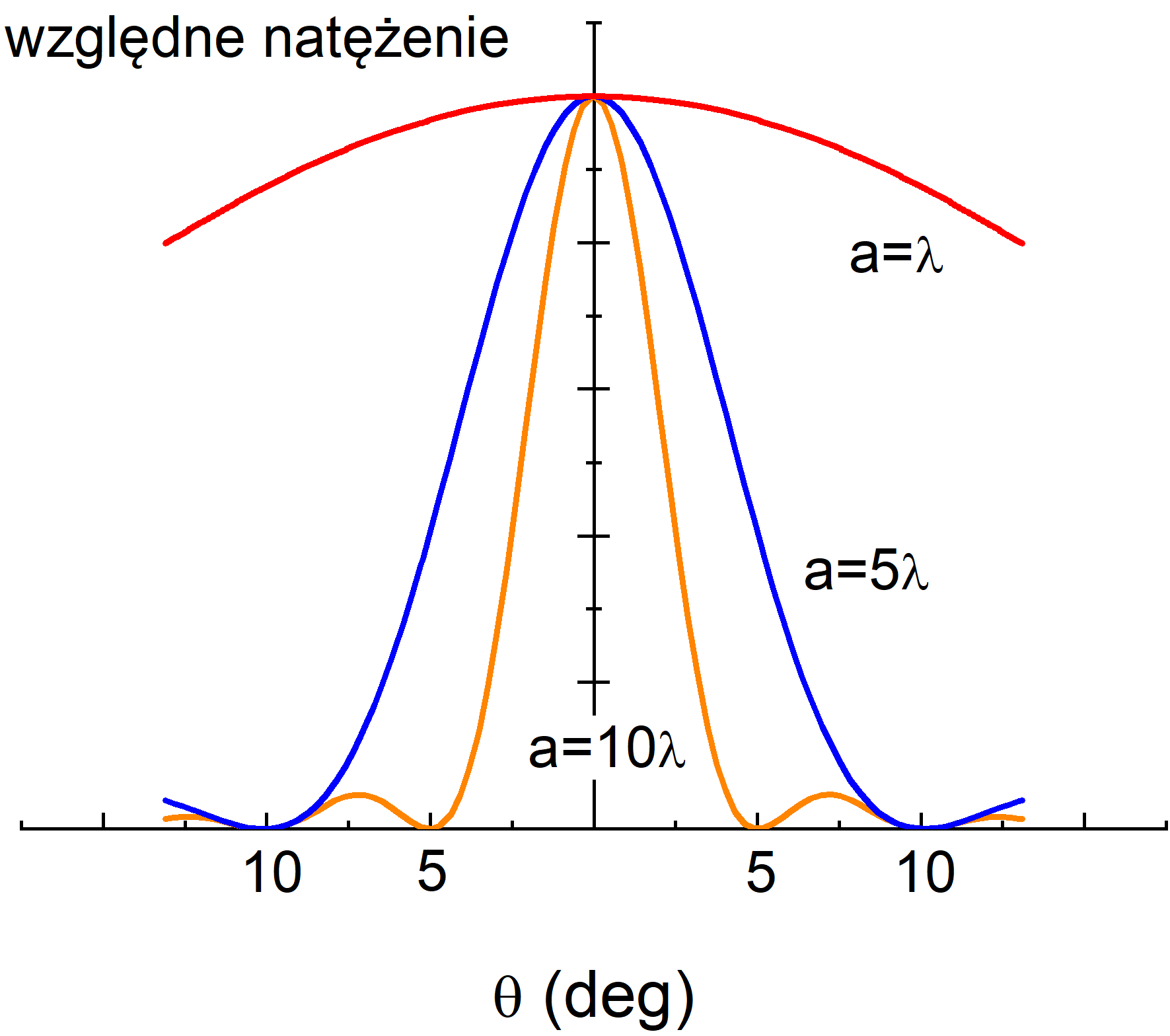
 Rys. 30.4. Natężenie światła w obrazie dyfrakcyjnym pojedynczej szczeliny