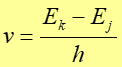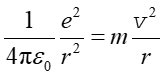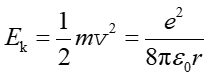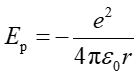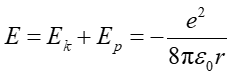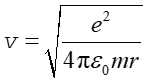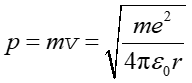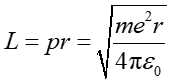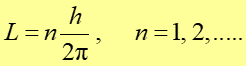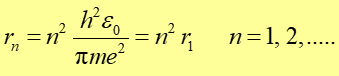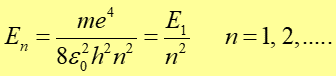Model Bohra atomu wodoru

33.3 Model Bohra atomu wodoru

Fizyka klasyczna przewidywała, że atom krążący po orbicie będzie wypromieniowywał energię, tak że częstość z jaką krąży elektron i w konsekwencji także częstość wysyłanego promieniowania będą się zmieniać w sposób ciągły. Tymczasem obserwujemy bardzo ostre linie widmowe o ściśle określonej częstotliwości (długości fali).

Sprzeczności te usunął Niels Bohr proponując nowy kwantowy model budowy atomu. Klasyczny obraz planetarnego atomu zbudowanego z masywnego jądra i krążących wokół niego pod wpływem siły kulombowskiej elektronów Bohr rozszerzył o nowe kwantowe postulaty:

Zamiast nieskończonej liczby orbit dozwolonych z punktu widzenia mechaniki klasycznej, elektron może poruszać się tylko po pewnych dozwolonych orbitach.

Podobnie jak oscylatory Plancka, tak samo atom wodoru może znajdować się tylko w ściśle określonych stacjonarnych stanach energetycznych, w których, pomimo, że elektron doznaje przyspieszenia (poruszając się po orbicie) nie wypromieniowuje energii. Jego całkowita energia pozostaje stała.

Promieniowanie elektromagnetyczne zostaje wysłane tylko wtedy gdy elektron poruszający się po orbicie o całkowitej energii E_j zmienia swój ruch skokowo, tak że porusza się następnie po orbicie o niższej energii E_k (rysunek 33.3 poniżej).

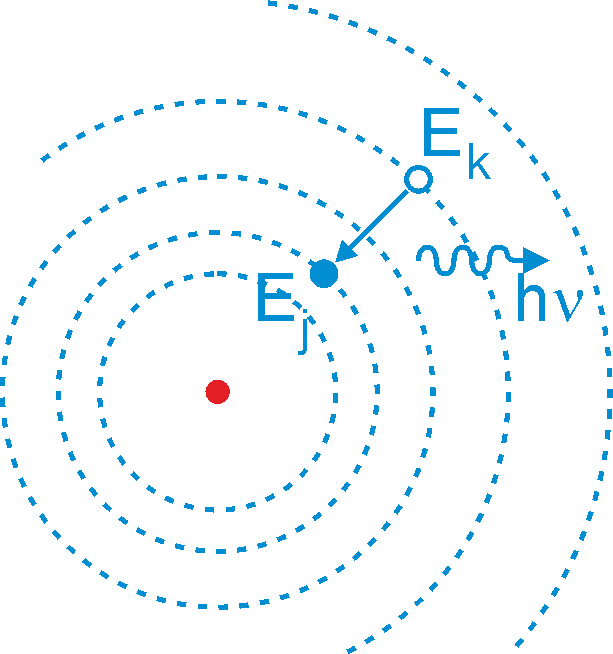
Rys. 33.3. Emisja fotonu przy zmianie orbity elektronu

Częstotliwość emitowanego promieniowania jest równa:

<(33.1)

Natomiast hv jest energią fotonu, który zostaje w trakcie przejścia wypromieniowany przez atom. Zwróćmy uwagę, że taki był postulat Einsteina głoszący, że częstotliwość fotonu promieniowania elektromagnetycznego jest równa energii fotonu podzielonej przez stałą Plancka.

Wynika stąd, że trzeba wyznaczyć energie stanów stacjonarnych i wtedy obliczając możliwe różnice tych energii będzie można przewidzieć wygląd widma promieniowania emitowanego przez atom.

W tym celu zakładamy, że elektron porusza się po orbitach kołowych o promieniu r ze środkiem w miejscu jądra oraz że jądro (pojedynczy proton) jest tak ciężkie, że środek masy pokrywa się ze środkiem protonu. Korzystając z drugiej zasady dynamiki Newtona i (prawa Coulomba) otrzymujemy

(33.2)

uwzględniliśmy tylko przyciąganie elektrostatyczne pomiędzy dodatnim jądrem i ujemnym elektronem zaniedbując oddziaływanie grawitacyjne.

Ćwiczenie
Żeby sprawdzić słuszność tego założenia oblicz stosunek sił przyciągania grawitacyjnego do elektrostatycznego dla protonu i elektronu w atomie wodoru. Masa elektronu m_e = 9.1·10⁻³¹ kg, masa protonu m_p = 1.7·10⁻²⁷ kg, ładunek elementarny e = 1.6·10⁻¹⁹ C, stała grawitacyjna G = 6.67·10⁻¹¹ Nm²/kg², a stała w prawie Coulomba 1/4πε₀ = 8.99·10⁹ Nm²/C². Sprawdź obliczenia i wynik.

Na podstawie wzoru (33.3) można obliczyć energię kinetyczną elektronu

(33.3)

Natomiast energia potencjalna układu elektron-proton jest dana równaniem

(33.4)

Ćwiczenie
Oblicz teraz stosunek energii kinetycznej do energii potencjalnej elektronu i odpowiedz od czego on zależy. Sprawdź obliczenia i wynik.

Całkowita energia układu będąca sumą energii kinetycznej i potencjalnej wynosi

(33.5)

Ze wzoru (33.3) na energię kinetyczną możemy wyznaczyć prędkość liniową elektronu

(33.6)

Na tej podstawie pęd elektronu dany jest równaniem

(33.7)

a moment pędu

(33.8)

Zwróćmy uwagę, że jeżeli znamy promień orbity r, to znamy również pozostałe wielkości E_k, E_p, E, v, p, oraz L.

Oznacza to również, że jeżeli jakakolwiek z tych wielkości jest skwantowana (może przyjmować tylko ściśle określone, a nie dowolne wartości), to wszystkie wymienione wielkości też muszą być skwantowane.

Bohr poszukiwał zasady, która dopuszczałaby tylko pewne promienie orbit, czyli tylko pewne wartości energii elektronów i wysunął hipotezę, według której najprostszą jest kwantyzacja parametrów orbity i która mówiła, że moment pędu elektronu musi być całkowitą wielokrotnością stałej Plancka podzielonej przez 2π. Podsumowując, postulaty Bohra dotyczące atomu były następujące:.

Elektron w atomie porusza się po orbicie kołowej pod wpływem przyciągania kulombowskiego pomiędzy elektronem i jądrem i ruch ten podlega prawom mechaniki klasycznej.

Zamiast nieskończonej liczby orbit, dozwolonych z punktu widzenia mechaniki klasycznej, elektron może poruszać się tylko po takich orbitach, dla których moment pędu L jest równy całkowitej wielokrotności stałej Plancka podzielonej przez 2π.

(33.9)

gdzie stała n jest liczbą kwantową .

Pomimo, że elektron doznaje przyspieszenia (poruszając się po orbicie), to jednak nie wypromieniowuje energii. Zatem jego całkowita energia pozostaje stała.

Promieniowanie elektromagnetyczne zostaje tylko wysłane gdy elektron poruszający się po orbicie o całkowitej energii E_k zmienia swój ruch skokowo, tak że porusza się następnie po orbicie o energii E_j. Częstotliwość emitowanego promieniowania jest równa .

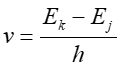Postulat Bohra dotyczy kwantyzacji momentu pędu L (równanie 33.9). Ale jak już mówiliśmy jeżeli jakakolwiek z wielkości E_k, E_p, E, v, p, L jest skwantowana, to wszystkie muszą być skwantowane.

Łącząc wyrażenie na moment pędu (33.8) z postulatem Bohra (33.9), otrzymujemy>

<(33.10)

Widzimy jak skwantowane jest r. Podstawiając ten wynik do wyrażenia na energię całkowitą (33.5) otrzymujemy wartości energii dozwolonych stanów stacjonarnych

(33.11)

To równanie przedstawia wartości energii dozwolonych stanów stacjonarnych.

Stan z liczbą kwantową n = 1 tzw. stan podstawowy odpowiada najniższej energii E₁ = −13.6 eV, a stan z liczbą kwantową n → ∞ odpowiada stanowi o zerowej energii E = 0, w którym elektron jest całkowicie usunięty poza atom.

Jak widać wprowadzenie kwantowania orbitalnego momentu pędu elektronu prowadzi do kwantowania jego energii całkowitej.

Ćwiczenie
Jakie są, zgodnie z teorią Bohra, wartości: promienia orbity, energii kinetycznej, energii potencjalnej, prędkości liniowej i prędkości kątowej elektronu w stanie podstawowym (n = 1) atomu wodoru? Sprawdź obliczenia i wynik.