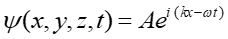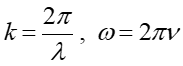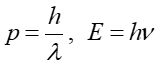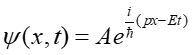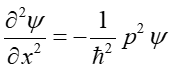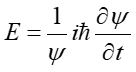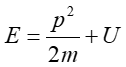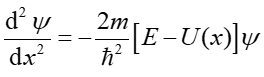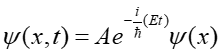Równanie Schrödingera

Przedstawione poniżej rozumowanie nie jest wyprowadzeniem równania Schrödingera, a ma na celu pokazanie, że można sformułować równanie rózniczkowe, które wiąże własności falowe i korpuskularne materii.

Według hipotezy de Broglie'a dualizmu korpuskularno-falowego każda cząstka kwantowa, taka jak np. elektron, jest reprezentowana przez falę materii, której amplituda określa prawdopodobieństwo znalezienia cząstki. Funkcję falową dla swobodnej cząstki możemy zapisać w postaci

(1)

Powyższa funkcja zespolona jest kombinacją liniową funkcji sin(kx−ωt) i cos(kx−ωt), za pomocą których opisywaliśmy rozchodzenie się fal (patrz rozdział 13). Przypomnijmy tu, że sens fizyczny ma kwadrat (modułu) funkcji falowej, który jest liczbą rzeczywistą.

Korzystając z podanych wcześniej zależności określonych równaniami (13.7)

(2)

oraz danych wyrażeniami (32.11) i (34.7)

(3)

możemy przekształcić funkcję falową (1) do postaci

(4)

Teraz, podobnie jak przy wyprowadzeniu równania ruchu falowego (równanie 13.15) wyjdziemy od tego ogólnego równania fali i obliczymy odpowiednie pochodne względem czasu i względem współrzędnej x

(5)

oraz

(6)

skąd otrzymujemy wyrażenia

(7)

oraz

(8)

Podobnie jak przy określaniu postaci równania falowego, szukamy równania różniczkowego, którego rozwiązaniem jest funkcja falowa (4).

W tym celu skorzystamy z klasycznego wzoru na energię całkowitą nierelatywistycznej cząstki

(9)

gdzie p²/2m jest energią kinetyczną cząstki, a U jej energią potencjalną.

Podstawiając za E i p odpowiednie wyrażenia (7) i (8) oraz mnożąc obustronnie przez ψ uzyskujemy jednowymiarowe równanie Schrödingera zależne od czasu

(10)

W przypadku stacjonarnym, gdy energia potencjalna U nie zależy od czasu to równanie przyjmuje postać podaną już wyrażeniem (35.4)

(11)

a funkcja falowa może być wyrażona w postaci

(12)