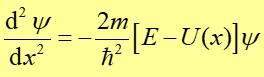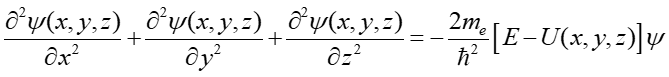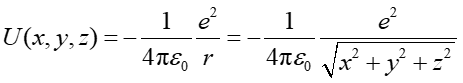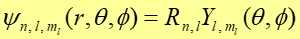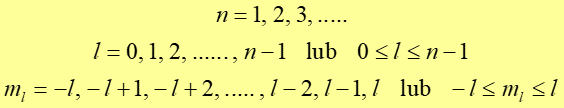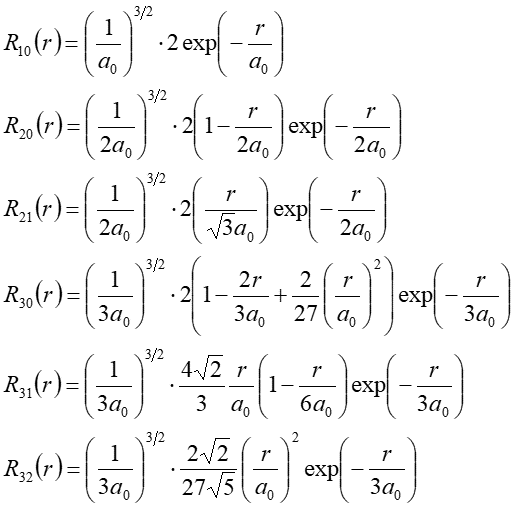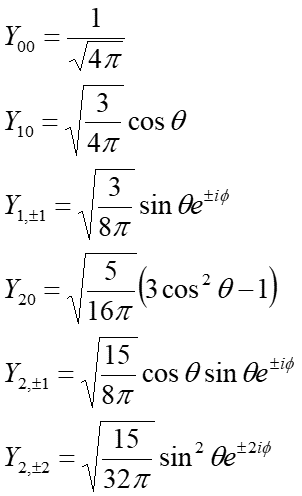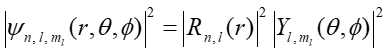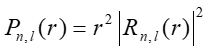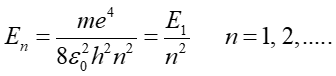35. Elementy mechaniki kwantowej
• Spis treści  
• Podsumowanie  
•   Teoria Schrödingera atomu wodoru

35.3 Teoria Schrödingera atomu wodoru

Równanie Schrödingera

  Znajomość ścisłej postaci funkcji falowej jest niezbędna do określenia ruchu cząstek w konkretnych przypadkach (zjawiskach fizycznych). Przykładem może być funkcja falowa ψ, opisująca ruch cząstki swobodnej, która została przedstawiona w paragrafie 35.1.

Taką ścisłą postać funkcji falowej dla dowolnego układu można znaleźć rozwiązując równanie Schrödingera. Jest to równanie różniczkowe opisujące zachowanie się układu kwantowego w czasie i przestrzeni, które w szczególności przyjmuje postać

gdzie E jest energią całkowitą cząstki, U(x) jej energią potencjalną zależną od jej położenia, a .

Zależność (35.4) przedstawia najprostszą formę równania Schrödingera to jest równanie w jednym wymiarze i niezależne od czasu.

Rozwiązanie równania Schrödingera polega na znalezieniu postaci funkcji falowej ψ i wartości energii cząstki E przy znanej działającej na cząstkę sile zadanej poprzez energię potencjalną U.

 Więcej o ...  Równaniu Schrödingera.  Więcej o ...  Przykładach rozwiązań równania Schrödingera.

Kwantowomechaniczny opis atomu wodoru

  Omówimy teraz zastosowanie teorii Schrödingera do atomu wodoru. Ten przypadek ma szczególne znaczenie, gdyż był to pierwszy układ, do którego Schrödinger zastosował swoją teorię kwantową i który stanowił pierwszą jej weryfikację.

Ponieważ atom wodoru jest układem trójwymiarowym równanie Schrödingera dla atomu wodoru ma bardziej skomplikowaną postać niż podane wcześniej równanie (35.4)

gdzie ψ = ψ(x,y,z).

Zgodnie z równaniem (19.4) energia potencjalna dwóch ładunków punktowych (elektronu i protonu) znajdujących się w odległości r jest dana wyrażeniem

Równanie Schrödingera  (35.5) rozwiązuje się zazwyczaj we współrzędnych sferycznych ze względu na to że energia potencjalna oddziaływania elektronu z jądrem (równanie 35.6) zapisana we współrzędnych sferycznych jest funkcją tylko jednej zmiennej (r) podczas gdy we współrzędnych prostokątnych funkcją wszystkich trzech współrzędnych (x,y,z).

Na rysunku 35.1 pokazane są współrzędne prostokątne (x, y, z) i współrzędne sferyczne (r, θ, ϕ) punktu P.

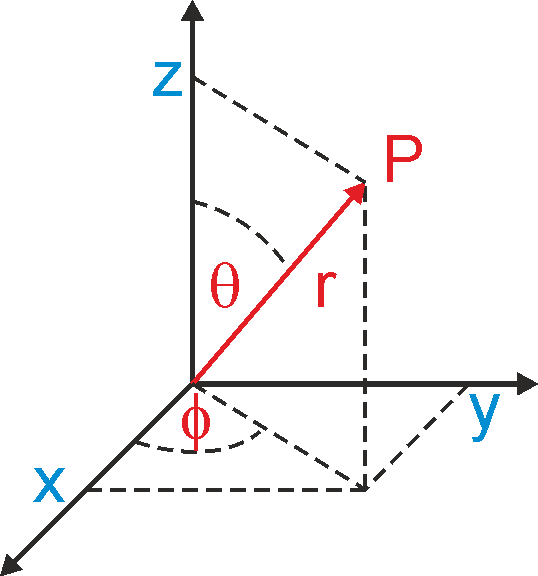
 Rys. 35.1. Związek pomiędzy współrzędnymi prostokątnymi (x, y, z)
i współrzędnymi sferycznymi (r, θ, φ) punktu P

Rozwiązanie równania Schrödingera w trzech wymiarach jest problem trudnym matematycznie między innymi ze względu na obliczenia w trzech wymiarach. Dlatego nie będziemy go rozwiązywać, a jedynie omówimy wybrane rozwiązania tego równania dla atomu wodoru.

Funkcje falowe

Okazuje się, że we współrzędnych sferycznych można funkcję falową przedstawić najogólniej  jako iloczyn dwóch funkcji: funkcji radialnej R(r) zależnej tylko od promienia r oraz funkcji kątowej Υ (θ, ϕ) zależnej tylko od kątów.

Rozwiązując równanie Schrödingera dla atomu wodoru stwierdzamy, że funkcja falowa elektronu zależy od trzech liczb całkowitych - liczb kwantowych n, l, m_l.

Przypomnijmy, że w dotychczas prezentowanych modelach atomu wodoru, zarówno energia elektronu jak i długość stojącej fali materii stowarzyszonej z elektronem zależały od jednej liczby kwantowej n.

Tak jest w przypadku ruchu w jednym wymiarze. Jednak trójwymiarowa funkcja falowa zależy od trzech liczb kwantowych co wynika z faktu, że ruch cząstki w przestrzeni jest opisany przez trzy niezależne zmienne; na każdą współrzędną przestrzenną przypada jedna liczba kwantowa.

Te trzy liczby kwantowe oznaczane n,l, m_l spełniają następujące warunki:

Ze względu na rolę jaką odgrywa liczba w określeniu energii całkowitej atomu, jest nazywana główną liczbą kwantową . Liczba l nosi nazwę azymutalnej liczby kwantowej , a liczba m_l nazywana jest magnetyczną liczbą kwantową .

Równanie Schrödingera ma poprawne fizycznie rozwiązania tylko dla liczb kwantowych spełniających warunki (35.8).

Z tych warunków widać, że dla danej wartości n (danej energii) istnieje na ogół kilka różnych możliwych wartości l, m_l.

Kilka pierwszych funkcji radialnych R(r) ma postać

a funkcji kątowych Υ (θ, ϕ)

Zgodnie z interpretację Borna związek pomiędzy falą materii i związaną z nią cząstką wyraża się poprzez kwadrat modułu funkcji falowej IψI², który wyraża gęstość prawdopodobieństwa znalezienia cząstki w danym punkcie przestrzeni

Na rysunku 35.2 pokazane są (dla kilku stanów kwantowych) wykresy radialnej gęstości prawdopodobieństwa, danej  wyrażeniem

(Czynnik r² w powyższym równaniu wynika stąd, że prawdopodobieństwo znalezienia elektronu w obszarze pomiędzy r i r+dr, w trzech wymiarach, jest proporcjonalne do elementarnej objętości r²dr.)

Na osi x odłożona jest odległość elektronu od jądra r podzielona przez promień pierwszej orbity Bohra r₁, natomiast na osi y przyjęto jednostki umowne.

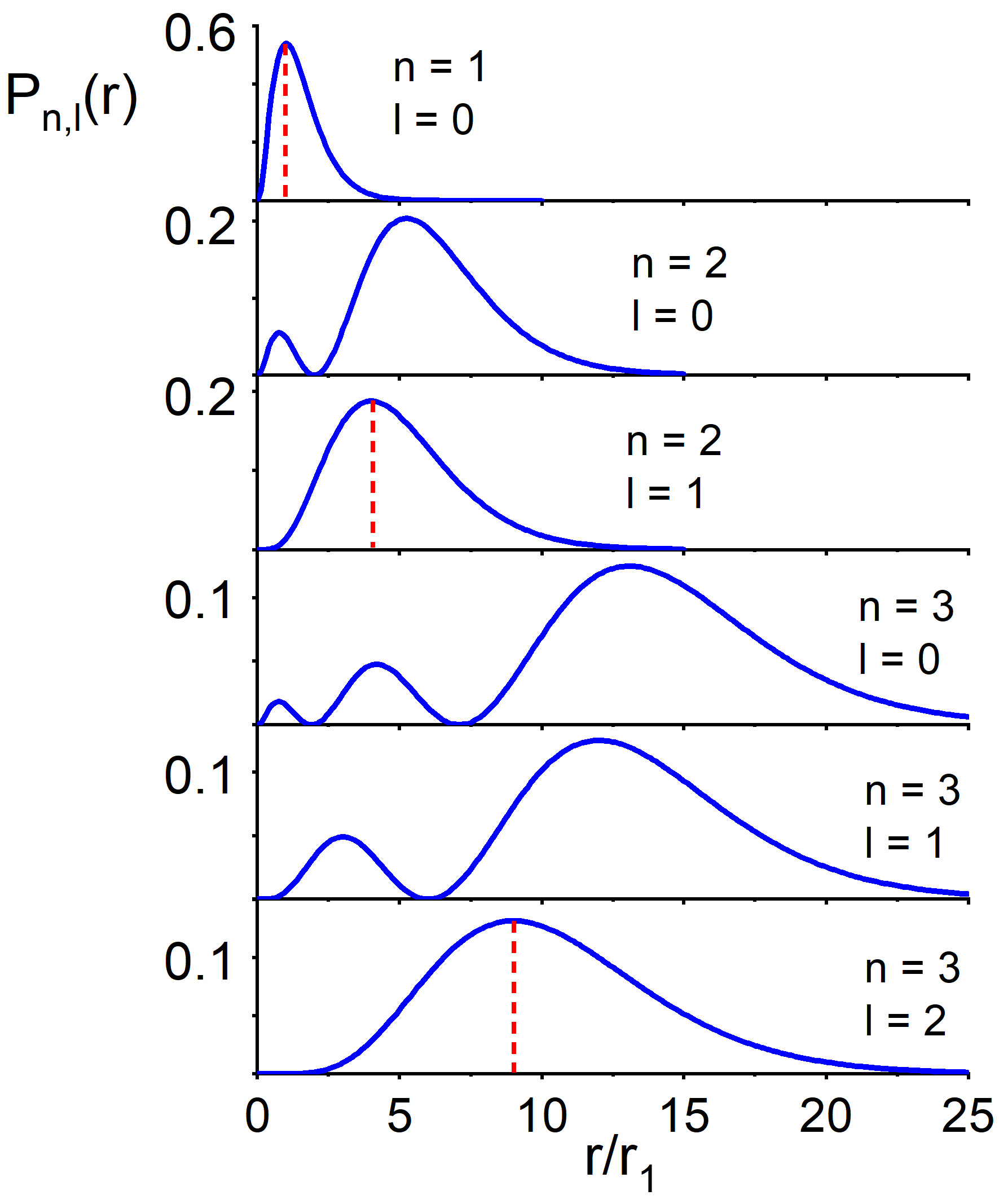
 Rys. 35.2. Radialna gęstość prawdopodobieństwa dla elektronu w atomie wodoru dla n = 1, 2, 3

Maksima gęstości prawdopodobieństwa, zaznaczone linią przerywaną, odpowiadają promieniom orbit w modelu Bohra dla n =1, 2, 3 (r_n = r₁n²).

Kątową gęstość prawdopodobieństwa IΥ(θ, ϕ)I² też można przedstawić graficznie w postaci tak zwanych wykresów biegunowych .

Na rysunku 35.3 pokazane są wykresy biegunowe gęstości prawdopodobieństwa dla kilku stanów kwantowych atomu wodoru.

Początek takiego wykresu umieszczamy w punkcie r = 0 (jądro), a kąt θ mierzymy od osi pionowej (z). Dla danej wartości kąta θ punkt wykresu leży w odległości (mierzonej pod kątem θ) równej IΥ(θ, ϕ)I² od początku układu tak jak to zaznaczono na jednym z wykresów.

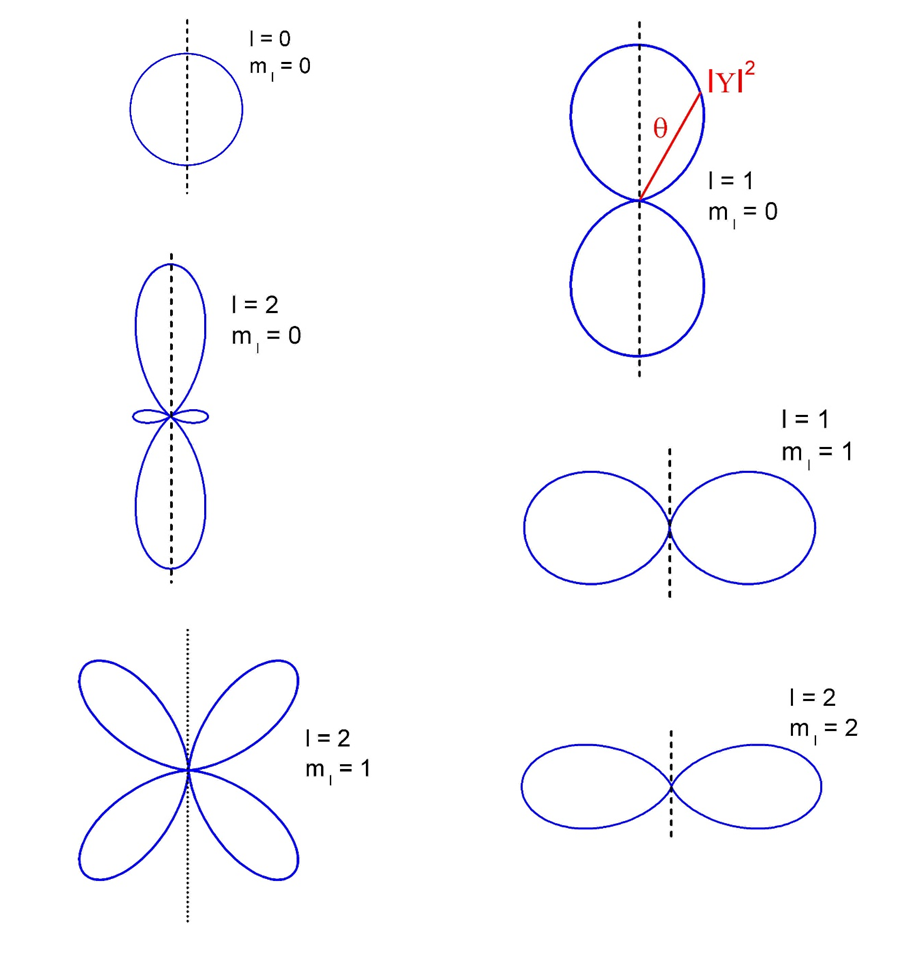
 Rys. 35.3. Kątowa gęstość prawdopodobieństwa dla elektronu w atomie wodoru dla l = 0,1, 2

Obraz przestrzenny otrzymujemy przez obrót wykresów biegunowych wokół pionowej osi (układ jest symetryczny ze względu na kąt ϕ).

Kątowe rozkłady prawdopodobieństwa (takie jak na rysunku 35.3) noszą nazwę orbitali . Do oznaczenia orbitali stosuje się litery: l = 0 - orbital s,
l = 1 - orbital p, l = 2 - orbital d, l = 3 - orbital f, itd.

Orbitale można traktować jako rozkłady ładunku elektronu wokół jądra. Gdy mówimy, że jądro atomowe jest otoczone chmurą elektronową mamy właśnie na myśli orbitale.

Energia elektronu

  Rozwiązanie równania Schrödingera dla atomu wodoru dostarcza oprócz funkcji falowych również wartości energii elektronu związanego w atomie. Te energie wyrażają się wzorem

Otrzymane wartości są identyczne z przewidywaniami modelu Bohra i wartościami obserwowalnymi doświadczalnie. Wynik ten stanowił pierwszą weryfikację teorii Schrödingera.

Teoria Schrödingera atomu jednoelektronowego ma ogromne znaczenie, bo podając obraz struktury atomu stworzyła podstawy kwantowego opisu wszystkich atomów wieloelektronowych, cząsteczek oraz jąder atomowych.

Opis falowy mikroświata jest już dzisiaj dobrze ugruntowaną teorią, a rozwój technik eksperymentalnych takich jak np. skaningowy mikroskop tunelowy pozwala na prowadzenie badań w świecie atomów.

Ten rozdział kończy moduł dziesiąty; możesz teraz przejść do podsumowania i zadań testowych.