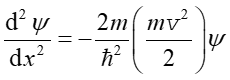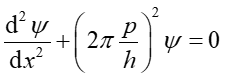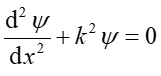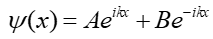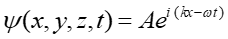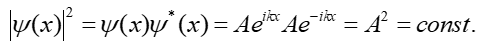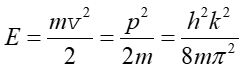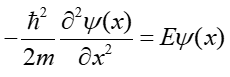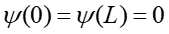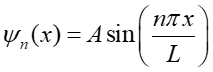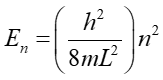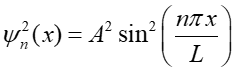Przykłady rozwiązań równania Schrödingera
Cząstka swobodna
Jeżeli wypadkowa siła działająca na cząstkę jest równa zero to również energia potencjalna U jest równa zero i całkowita energia cząstki jest jej energią kinetyczną. Załóżmy, że cząstka porusza się w kierunku odatnich wartości osi x to wtedy równanie (35.4) przyjmuje postać
|
(1) |
i można je, korzystając z wyrażenia na pęd cząstki, p = mv, przepisać jako
|
(2) |
Podstawiając, na podstawie równania (34.2), ![]() otrzymujemy
otrzymujemy
|
(3) |
gdzie ![]() jest liczbą falową.
jest liczbą falową.
Ogólne rozwiązanie równania (3) ma postać:
|
(4) |
gdzie A i B są stałymi. Uwzględniając część funkcji falowej zależnej od czasu możemy zapisać funkcję falową cząstki swobodnej
|
(5) |
gdzie uwzględniono, że w naszym przypadku B = 0, bo drugi wyraz w równaniu (4) opisuje falę rozchodzącą się w kierunku –x, podczas gdy cząstka porusza się w kierunku +x. Możemy teraz obliczyć gęstość prawdopodobieństwa
|
(6) |
Widzimy, że prawdopodobieństwo znalezienia cząstki swobodnej w każdym punkcie toru ruchu jest jednakowe.
Natomiast wartości własne wynoszą w tym przypadku
|
(7) |
gdzie uwzględniono zależności ![]() oraz
oraz ![]() .
.
Cząstka w (1-wymiarowej) studni potencjału
Rozpatrzymy teraz prosty przypadek cząstki poruszającej się w jednowymiarowej, nieskończonej studni potencjału o szerokości L (rysunek poniżej).
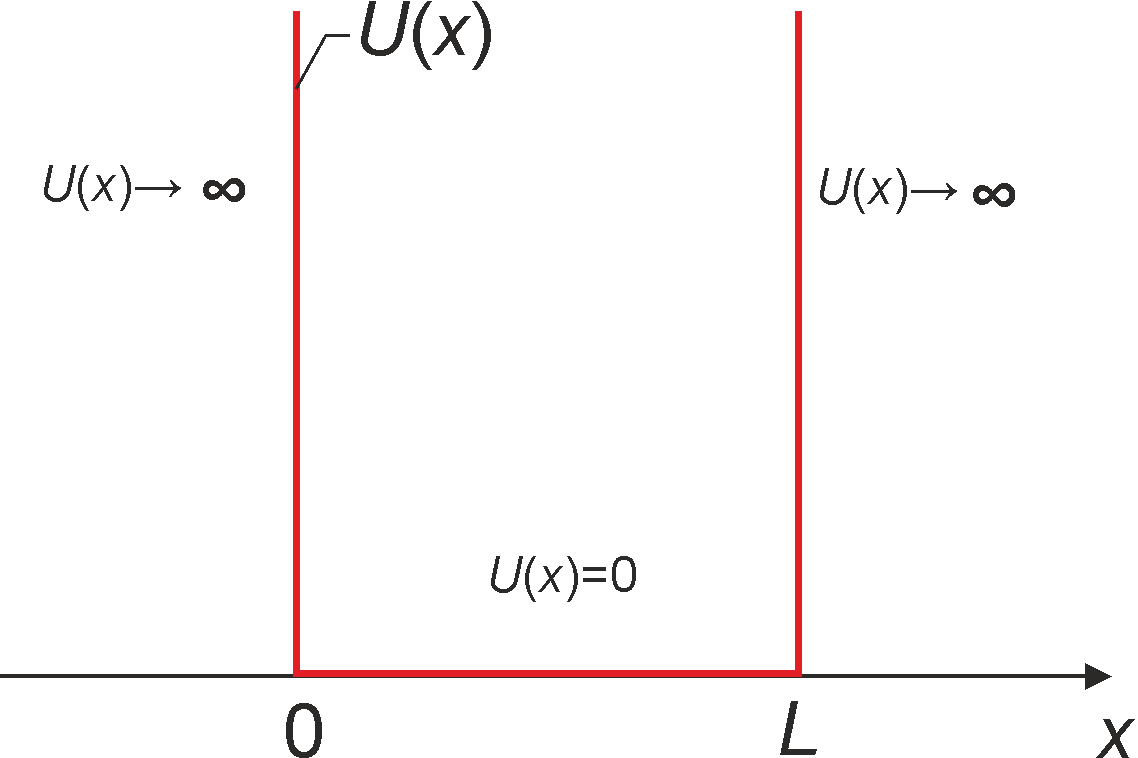
Rys. 1. Jednowymiarowa, nieskończona studnia potencjału o szerokości L.
Potencjał wynosi zero wewnątrz studni i zmierza do nieskończoności na zewnątrz studni
|
(8) |
Ponieważ poza obszarem 0 < x < L, U(x) → ∞ więc prawdopodobieństwo znalezienia cząstki poza obszarem gdzie U(x) = 0 jest równe zeru, co można zapisać w postaci warunków brzegowych
|
(9) |
Rozwiązaniem równania Schrödingera (8) przy warunkach brzegowych (9) jest funkcja falowa
|
(10) |
gdzie n jest liczbą kwantową. To rozwiązanie jest analogiczne do równania opisującego falę stojącą w strunie zamocowanej na obu końcach.
Wstawiając to rozwiązanie do równania (8) otrzymujemy dyskretne wartości energii cząstki (wartości własne)
|
(11) |
Energia cząstki zamkniętej w studni potencjału może przyjmować jedynie dyskretne (skwantowane) wartości. Co więcej, cząstka nie może mieć zerowej energii kinetycznej,
co oznacza, że niemożliwe jest, aby ta cząstka była w spoczynku. Na rysunku poniżej pokazane są trzy pierwsze funkcje falowe cząstki w studni potencjału
i odpowiadające im stany energetyczne.
Rozkład gęstości prawdopodobieństwa znalezienia cząstki kwantowej w nieskończonej studni potencjału, w pobliżu punktu x jest dana wyrażeniem
|
(12) |
i jest również pokazana na rysunku poniżej
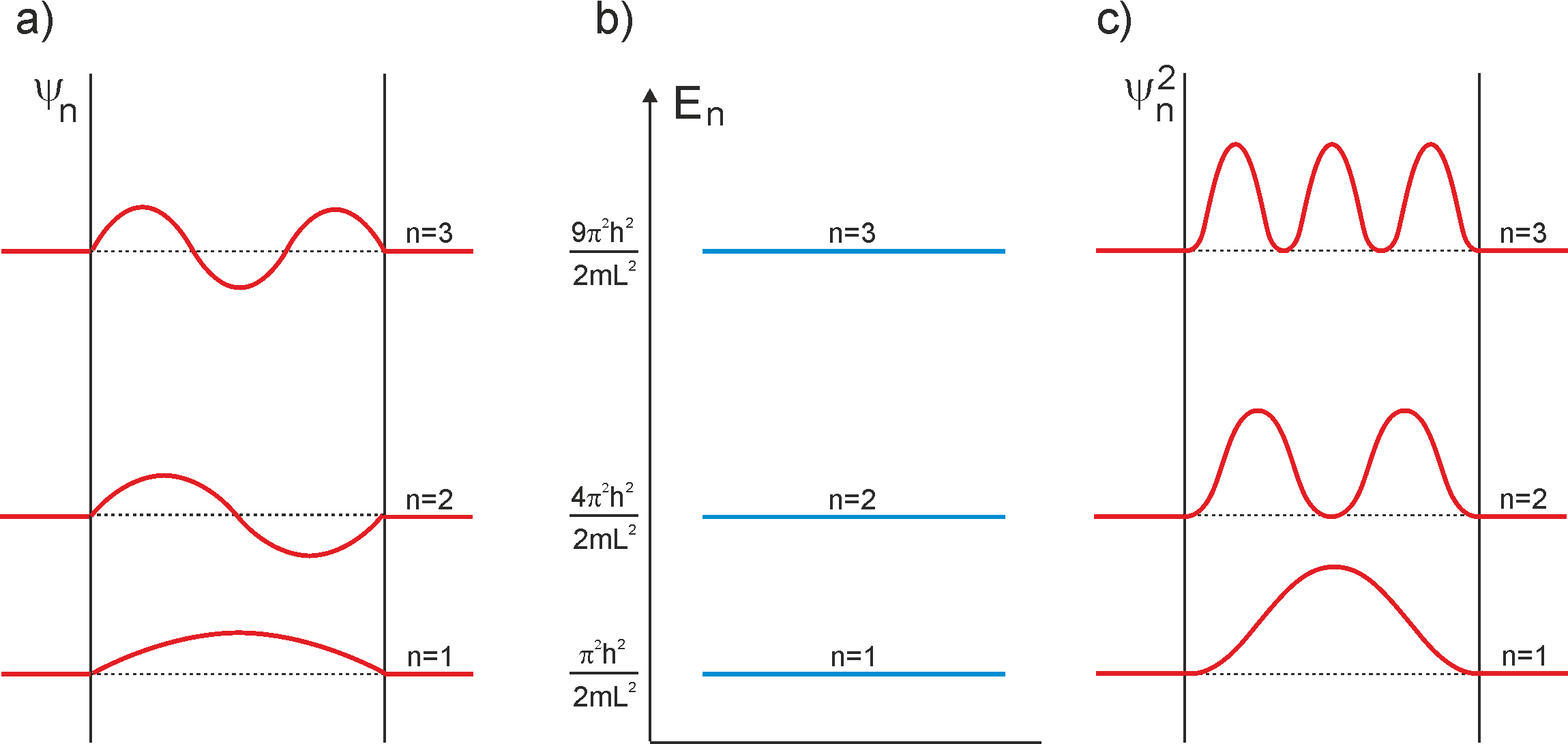
Rys. 2. Pierwsze trzy stany kwantowe cząstki w nieskończonej studni potencjału:
a) funkcje falowe (fale stojące), b) dozwolone stany energetyczne, c) rozkład gęstości prawdopodobieństwa
Widzimy, że gdy cząstka znajduje się w stanie podstawowym (n = 1), to najbardziej prawdopodobne jest znalezienie jej w środku studni. Rozkład gęstości prawdopodobieństwa ma tam największą wartość. Natomiast w przypadku pierwszego stanu wzbudzonego (n = 2) gęstość prawdopodobieństwa w środku studni ma wartość zero; cząstki nie znajdziemy w tym miejscu. Natomiast największe prawdopodobieństwo znalezienia jej występuje w dwóch miejscach gdzie rozkład prawdopodobieństwa ma maksima, co różni się od praw fizyki klasycznej.
Nieskończona studnia kwantowa jest obiektem teoretycznym. Na rysunku poniżej pokazana jest realistyczna sytuacja, możliwej do zrealizowania studni potencjału, w której energia potencjalna elektronu poza studnią ma skończoną wartość dodatnią U0, zwaną głębokością studni.
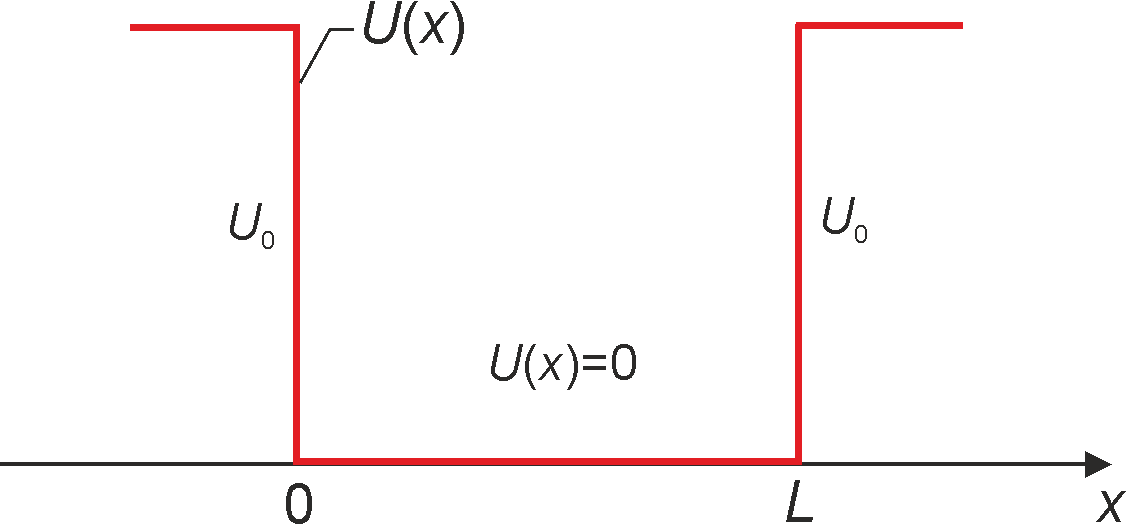
Rys. 3. Skończona studnia potencjału o szerokości L.
Potencjał wynosi zero wewnątrz studni i ma skończoną wartość U0 na zewnątrz studni
Wewnątrz studni, gdzie potencjał jest równy zeru, sytuacja jest analogiczna jak w nieskończonej studni potencjału;
wartości własne energii są w dalszym ciągu skwantowane i zależą od głębokości studni. Gdy energia cząstki jest większa od głębokości studni,
energie tworzą kontinuum (dozwolona jest każda wartość energii jak pokazano na rysunku poniżej).
Podstawowa różnica polega na tym, że funkcje własne nie znikają na granicy obszaru studni. Ponieważ studnia jest skończona, to cząstka może
nieco wniknąć w obszar zabroniony, pomimo „za małej” energii, a funkcja falowa zanika w tym obszarze ekspotencjalnie, tym wolniej,
im cząstka ma większą energię (rysunek poniżej).Znalezienie cząstki poza studnią ma skończone prawdopobieństwo, co w mechanice klasycznej jest niemożliwe.
Z tego typu potencjałami mamy, na przykład, do czynienia w półprzewodnikowych diodach, półprzewodnikowych laserach, kropkach kwantowych.
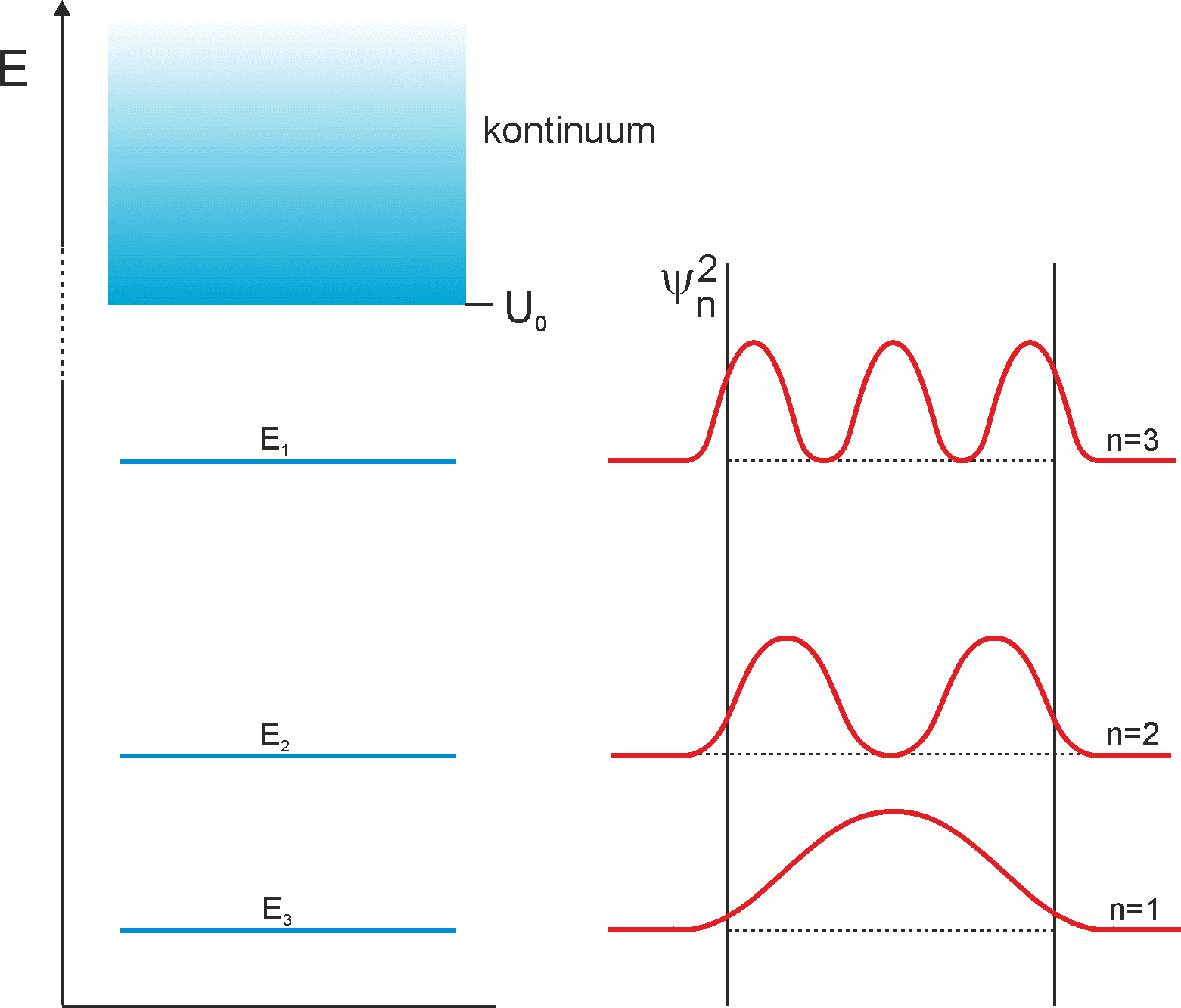
Rys. 4. Cząstka uwięziona w skończonej studni potencjału ma energie skwantowane n = 1, 2, 3 …nmax
Gdy E > U0 energia nie jest skwantowana. Rozkład gęstości prawdopodobieństwa - znalezienie cząstki poza studnią ma skończone prawdopobieństwo
Skoro cząstka może wniknąć w obszar zabroniony (klasycznie), to jeżeli ma on małą szerokość (jest dostatecznie wąski), cząstka może przeniknąć przez ten obszar, jest to wytłumaczenie efektu tunelowego.
Tunelowanie cząstki przez barierę potencjału
Zjawiskiem przewidywanym przez mechanikę kwantową, a niedopuszczalnym przez mechanikę klasyczną, jest zjawisko tunelowe, polegające na przenikaniu cząstek przez barierę potencjału o wysokości (energii) znacznie przekraczającej energię cząstki.
W mechanice klasycznej, żeby poknać barierę potencjału, na przykład pokonać wzgórze o wysokości h cząstka musi mieć energię kinetyczną większą od jej energii potencjalnej na wysokości h i wtedy na pewno znajdzie się po drugiej stronie wzgórza. Prawdopodobieństwo pokonania tej przeszkody, bariery jest więc równe 1. W przeciwnej sytuacji (Ek < mgh) cząstka nie pokona bariery, nie wjedzie na szczyt, pozostanie po tej stronie wzgórza, a prawdopodobieństwo znalezienia jej po drugiej stronie wzgórza równe jest 0.
Natomiast w fizyce kwantowej taka cząstka (o energii mniejszej od energii bariery), może wniknąć w obszar zabroniony i z pewnym prawdopodobieństwem może znaleźć się po drugiej stronie bariery. Co więcej cząstka o energii większej od bariery nie zawsze musi przejść nad barierą; może, z pewnym prawdopodobieństwem, odbić się od bariery i zawrócić, co w mechanice klasycznej jest niemożliwe. Ta sytuacja jest zobrazowana na rysunku poniżej.
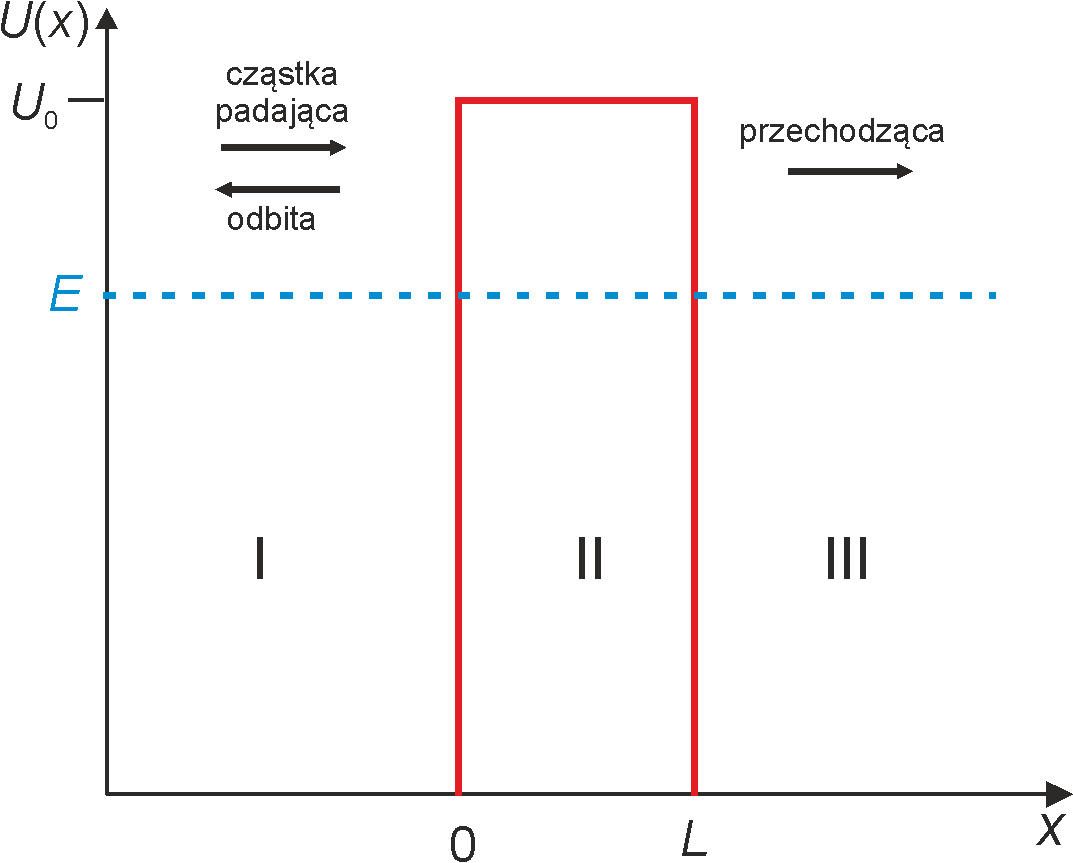
Rys. 5. Tunelowanie cząstki przez barierę potencjału U0.
Oznacza to, że funkcje falowe odpowiadające cząstce zachowują się inaczej w przed barierą potencjału, w jej obszarze i za barierą potencjału. Żeby zbadać pokonywanie bariery potencjału przez funkcję falową należy rozwiązać równanie Schrödingera. W obszarach poza barierą potencjału (I i III), gdzie cząstka porusza się swobodnie, rozwiązania mają charakter oscylujący, a zanikający wykładniczo w obszarze bariery (II). Rozwiązania dla trzech wymienionyc obszarów pokazane zostały na rysunku poniżej.
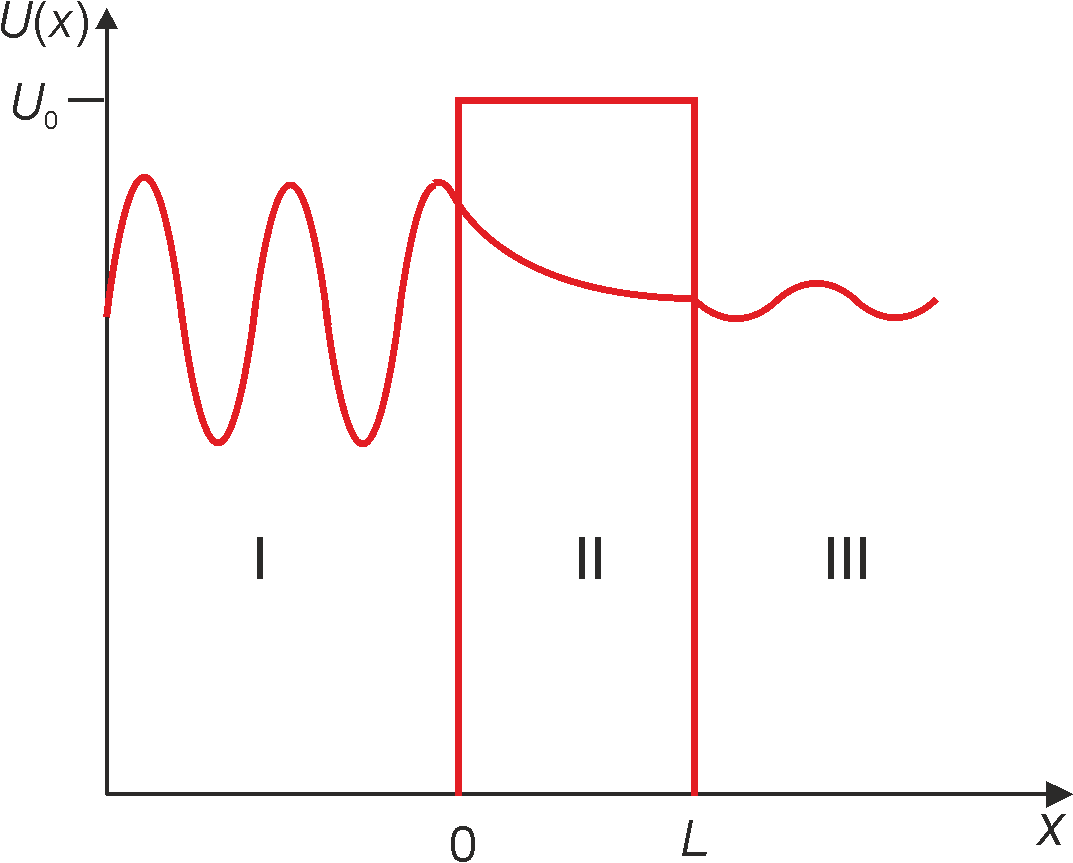
Rys. 6. Rozwiązania stacjonarnego rownania Schrödingera dla tunelującej cząstki w obszarzach I, II i III.
We współczesnej technice zjawisko tunelowe jest wykorzystywane w półprzewodnikowych elementach elektronicznych takich jak dioda tunelowa oraz w urządzeniach takich jak skaningowy mikroskop tunelowy. Fuzja jądrowa w Słońcu zachodzi w dużym stopniu dzięki zjawisku tunelowemu.


 Teoria Schrödingera atomu wodoru
Teoria Schrödingera atomu wodoru