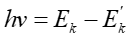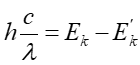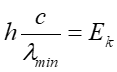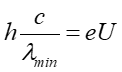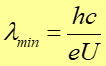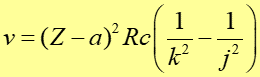36. Atomy wieloelektronowe
• Spis treści  
• Lasery  
•   Układ okresowy pierwiastków

36.4 Promieniowanie X

  W poprzednich wykładach mówiliśmy już o zastosowaniu promieniowania rentgenowskiego. Teraz poznamy więcej szczegółów dotyczących widma tego promieniowania.

Na rysunku 36.5 poniżej pokazana jest lampa rentgenowska.

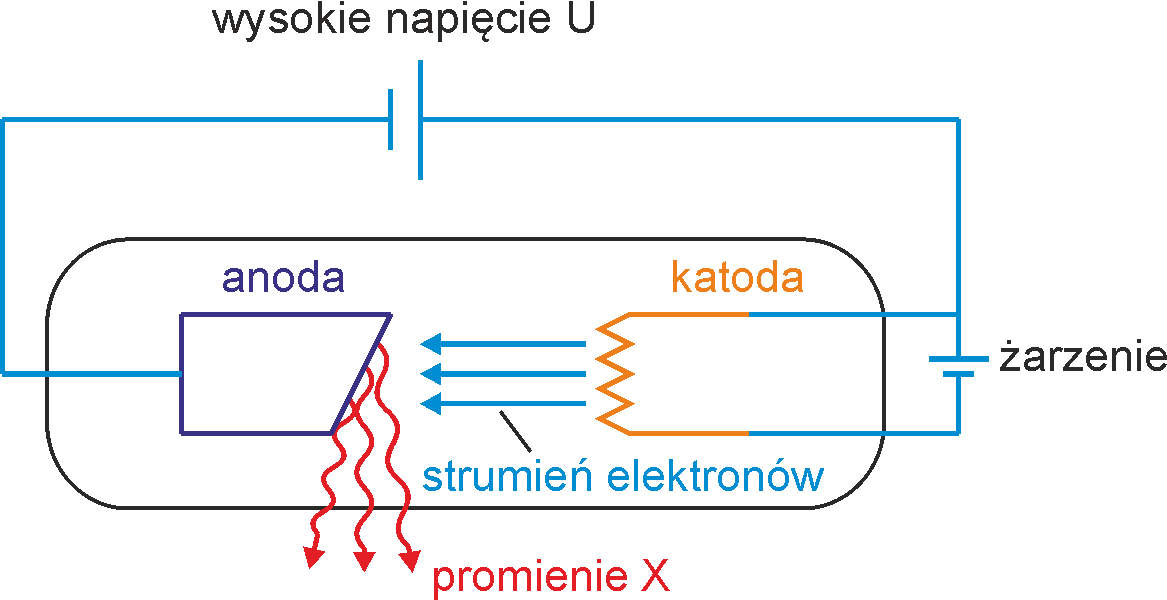
 Rys. 36.5. Schemat lampy rentgenowskiej

Elektrony emitowane z katody są przyspieszane przez wysokie napięcie rzędu 10⁴ V (przyłożone pomiędzy katodą i anodą) i uderzają w anodę (tarczę). W anodzie elektrony są hamowane aż do ich całkowitego zatrzymania.

Zgodnie z fizyką klasyczną, w wyniku tego hamowania powinna nastąpić emisja promieniowania elektromagnetycznego o widmie ciągłym ponieważ ładunek doznaje przyspieszenia (opóźnienia).

Przykładowy rozkład widmowy rentgenowski otrzymany dla wolframu jest pokazany na rysunku 36.5.

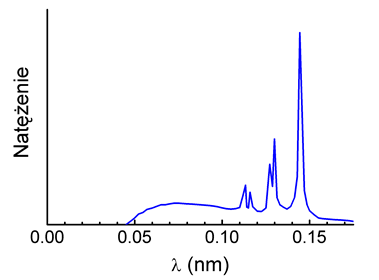
 Rys. 36.6. Widmo rentgenowskie wolframu

Najbardziej charakterystycznymi cechami obserwowanych rozkładów widmowych promieniowania X są:

• Charakterystyczne linie widmowe, to jest maksima natężenia promieniowania, występujące dla ściśle określonych długości fal. Zaobserwowano, że widmo liniowe zależy od materiału (pierwiastka) anody.


• Istnienie dobrze określonej minimalnej długości fali λ_min widma ciągłego. Stwierdzono, że wartość λ_min zależy jedynie od napięcia U i jest taka sama dla wszystkich materiałów, z jakich wykonana jest anoda.

Istnienie krótkofalowej granicy widma ciągłego promieniowania X nie może być wyjaśnione przez klasyczną teorię elektromagnetyzmu bo nie istnieją żadne powody, aby z anody nie mogły być wysłane fale o długości mniejszej od jakiejś wartości granicznej.

Jeżeli jednak potraktujemy promieniowanie rentgenowskie jako strumień fotonów to wyjaśnienie obserwowanego zjawiska jest proste. Elektron o początkowej energii kinetycznej E_k (uzyskanej dzięki przyspieszeniu napięciem U) w wyniku oddziaływania z ciężkim jądrem atomu tarczy (anody) jest hamowany i energia jaką traci pojawia się w formie kwantów (rysunek 36.7).

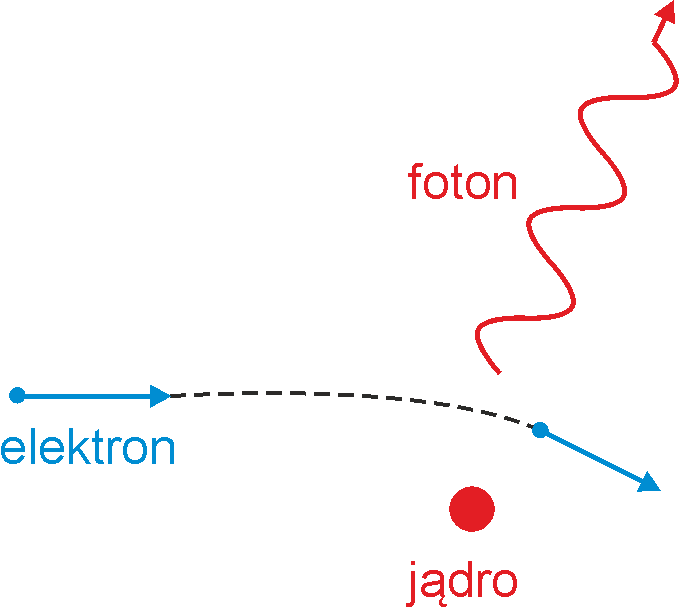
 Rys. 36.7. Oddziaływanie elektronu z atomem tarczy zmienia jego energię kinetyczną

Energia powstającego fotonu jest dana wzorem

gdzie E_k' jest energią elektronu po zderzeniu. Elektron w trakcie zderzenia przekazuje jądru pewną energię jednak ze względu na to, że jądra tarczy są bardzo ciężkie (w porównaniu do elektronu) możemy ją zaniedbać.

Długość fali fotonu można obliczyć z relacji

W wyniku zderzeń elektrony tracą różne ilości energii )typowo elektron zostaje zatrzymany w wyniku wielu zderzeń z jądrami tarczy) otrzymujemy więc szereg fotonów o różnych energiach (różnych λ). Wobec tego promieniowanie rentgenowskie wytwarzane przez wiele elektronów będzie miało widmo ciągłe.

Powstaje wiele fotonów o długościach od λ_min do λ → ∞, co odpowiada różnym energiom traconym w zderzeniach. Foton o najmniejszej długości fali λ_min  (zarazem maksymalnej energii) będzie emitowany wtedy gdy elektron straci całą energię w jednym procesie zderzenia. Oznacza to, że po tym zderzeniu E_k' = 0 więc

Ponieważ energia kinetyczna elektronu jest równa eU (elektron przyspieszony napięciem U) więc otrzymujemy związek

skąd

Tak więc minimalna długość fali odpowiadająca całkowitej zamianie energii kinetycznej elektronów na promieniowanie zależy jedynie od napięcia U, a nie zależy np. od materiału z jakiego zrobiono tarczę.

Podobnie na gruncie fizyki kwantowej można wyjaśnić powstawanie widma liniowego (charakterystycznego).

Elektron z wiązki padającej przelatując przez atom anody może wybić elektrony z różnych powłok atomowych. Na opróżnione miejsce (po wybitym elektronie) może przejść elektron z wyższych powłok. Towarzyszy temu emisja fotonu o ściśle określonej energii równej różnicy energii elektronu w stanie początkowym (przed przeskokiem) i stanie końcowym (po przeskoku). Z kolei powstało miejsce wolne tzw. dziura po elektronie, który przeskoczył na niższą powłokę. Miejsce to może być zapełnione przez kolejny elektron z wyższej powłoki itd.

Zazwyczaj proces powrotu atomu do stanu podstawowego składa się więc z kilku kroków przy czym każdemu towarzyszy emisja fotonu. W ten sposób powstaje widmo liniowe.

Częstotliwość (długość fali) promieniowania charakterystycznego możemy obliczyć korzystając ze wzoru analogicznego do wyrażenia (33.13), który podaliśmy dla atomu wodoru

gdzie R jest stałą Rydberga. We wzorze tym uwzględniono fakt, że w atomie wieloelektronowym elektron jest przyciągany przez jądro o ładunku +Ze, a równocześnie obecność innych elektronów osłabia to oddziaływanie. Efekt ten nazywamy ekranowaniem jądra i uwzględniamy go poprzez wprowadzenie stałej ekranowania a.

Widzimy, że częstotliwość promieniowania charakterystycznego jest proporcjonalna do kwadratu liczby atomowej Z więc jest charakterystyczna dla atomów pierwiastka anody. Ta zależność jest nazywana prawem Moseleya. Możemy się nią posłużyć przy analizie liniowych widm rentgenowskich w celu identyfikacji pierwiastków lub ich zawartości w badanym materiale.