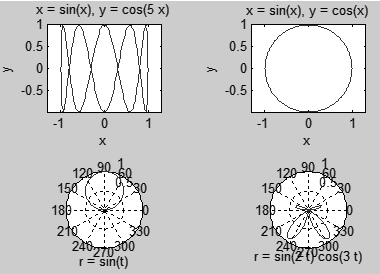
- ezplot('sin(x)', 'cos(5*x)')
- ezplot('sin(x)', 'cos(x)')
- ezpolar('sin(t)',[0 pi])
- ezpolar('sin(2*t).*cos(3*t)',[0 pi])

Wymagania wstępne:Znajomość materiału z wykładów i poprzednich ćwiczeń a w szczególności podstawowych poleceń oraz obsługi interfejsu IDE Matlaba (okna komend, edytora, systemu pomocy, sposobu uruchamiania programów). Cel ćwiczeń laboratoryjnych nr 2 to:1. utrwalenie wiadomości o poznanych poleceniach i umiejętności stosowania ich w prostych programach z pętlami i instrukcją IF;2. poznanie podstawowych sposobów tworzenia i modyfikowania wykresów XY oraz komunikacji z plikami dyskowymi. |
Cena=145.5;
while 1
x=input('Zgadnij cene:');
if x>Cena
fprintf('Za duzo!\n');
else
fprintf('Za malo! \n');
end
end
|
Przypomnienie:
Petla typu WHILE:
while wyrazenie
. . . . . instrukcje
end
powtarza wykonywanie instrukcji tak dlugo dopóki wyrazenie jest rózne od zera
B) Dokonaj następujących przeróbek programu:
A) Napisz program (pr3.m) z pętlą FOR...END, który wyświetla na ekranie liczby nieparzyste od 1 do 9 oraz ich pierwiastki w następującej postaci:
Liczba Pierwiastek 1 1.000 3 1.732 5 2.236 7 2.646 9 3.000 |
B) Zmodyfikuj ten program tak, aby oprócz wyświetlenia tabelki także wyprowadził ją do pliku o nazwie: PIERWIASTKI.TXT.
Możesz wyświetlić zawartość tego pliku poleceniem:
type 'Pierwiastki.txt'
Funkcje ezplot(...) oraz ezpolar(...) mają kilka postaci. Wyświetl ich opisy przy pomocy help.
Wykorzystaj funkcję subplot(lw,lk,nr) aby w jednym oknie graficznym wyświetlić 4 wykresy:
|

|
|
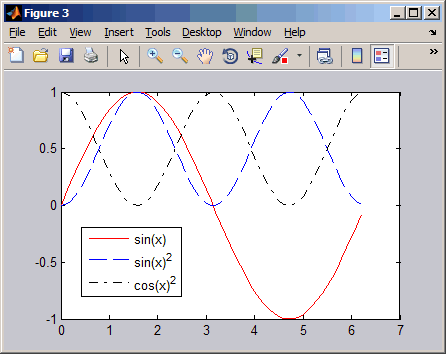
Przy pomocy funkcji plot, dla x z przedziału od 0 do 2*pi narysuj na jednym wykresie
trzy przebiegi funkcji: a) sin(x) - czerwoną linią ciągłą b) sin2(x) - niebieską linią kreskowaną c) cos2(x) - czarną linią typu kropka-kreska Dodaj legendę (opis wykresów) Objaśnienia masz w help plot oraz TUTAJ i tu |
|
Pomiary co 100 mm ugięcia płaskownika zamocowanego poziomo na jednym końcu i obciążonego pionową siłą na drugim zamieszczono w tabeli:
|
x |
0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
|
y |
0 |
-6.0 |
-6.2 |
-11.9 |
-12.4 |
-25.8 |
-31.1 |
-52.8 |
-66.8 |
Sporządź wykres według tej tabeli (linią kropkowaną z zaznaczeniem punktów z tabeli) a następnie zastosuj (zgodnie z opisem w Kompendium):
a = polyfit(x, y, n) gdzie: a - szukany wektor współczynników wielomianu, x , y - współrzędne danych punktów (np.: dane z pomiarów), n - stopień dopasowywanego wielomianu
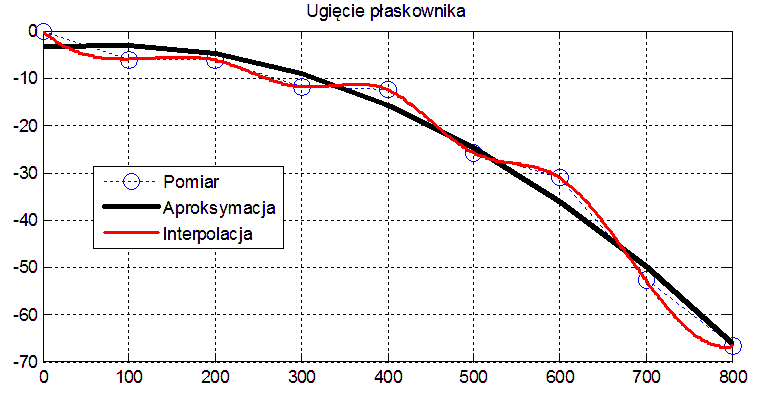
Która z tych operacji jest prawidłowa w tym przypadku jeśli wiadomo, że dane były obarczone błędami pomiaru?
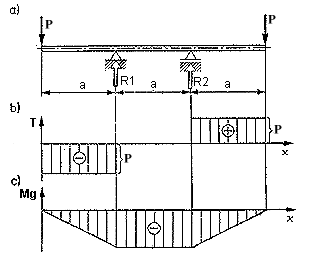
Dla zginanej belki (jak na rysunku) napisz program generujący wykresy siły tnącej T(x) oraz momentu gnącego Mg(x) w funkcji odległości x od początku belki.
Dane są: a, P. Program ma wczytać dane z klawiatury.
Tabela wartości x, T(x), Mg(x) ma być
generowana do pliku o nazwie BELKA1.TXT.
Podpowiedzi: użyj instrukcji FOR oraz IF.
Wykresy powinny być w osobnych układach współrzędnych.
|
Przedział |
Od |
Do |
Siła tnąca T |
Moment gnący Mg |
|
1 |
0 |
a |
T = -P |
Mg = -P· x |
|
2 |
a |
2a |
T = 0 |
Mg = -P· a |
|
3 |
2a |
3a |
T = P |
Mg = P· x - P·a |
Zadanie domowe nr 2:
1) Uogólnij program (z zad.5) tak aby działał dla danej długości belki L oraz danych dowolnych odległości podpór od początku belki: a i b .