W Matlabie można wiele działań na macierzach prowadzić bez użycia pętli - jak to pokazano w poprzednich ćwiczeniach - jednak uniwersalnym sposobem stosowanym we wszystkich językach programowania jest użycie podwójnej pętli.
Wówczas, przy generowaniu lub przetwarzaniu macierzy M posiadającej Lw wierszy i Lk kolumn, najczęściej stosujemy wybieranie poszczególnych elementów M(w,k) wiersza pierwszego a potem następnych, czyli indeksy wiersza w oraz kolumny k zmieniają się w sposób następujący:
dla w= 1, k=1, 2,...Lk;
dla w= 2, k=1, 2,...Lk;
. . . . . . . . . . .
dla w=Lw, k=1, 2,...Lk;
Jak widać pętla generująca wartości k musi być powtarzana tyle razy ile jest wierszy. Inaczej mówiąc petla zmieniająca numery kolumn k musi znaleźć się wewnątrz pętli zmieniającej numery wierszy w. W najprostszym przypadku może to wyglądać tak jak na rysunku poniżej:
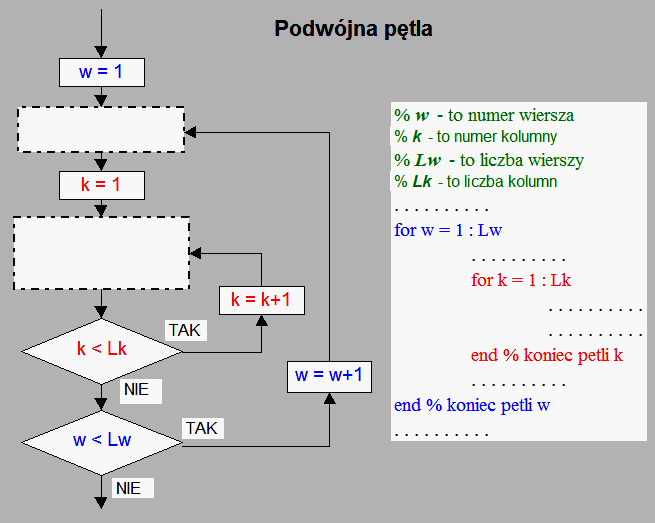
Przykład 1:
|
Wygenerować macierz: |
Analiza problemu |
1 5 9 13 3 7 11 15 5 9 13 17 7 11 15 19 |
Jak widać w każdym wierszu macierzy:
Po za tym oczywiście wskaźniki zarówno wiersza jak i kolumny muszą przyjmować kolejne wartości w zakresie liczb naturalnych (w naszym przypadku: 1, 2, 3, 4). |
Zadanie można oczywiście rozwiązać na wiele sposobów, z których pokazano dwa:
PROGRAM 1 opiera się na koncepcji generowania kolejnych wartości indeksów wierszy i kolumn w i k tak jak to przedstawiono powyżej. Następnie wartości elementów macierzy a(w,k) są tworzone z wyrażeń wykorzystujących te indeksy w i k:
% PROGRAM 1
clear;
for w=1:4
el=2*w-1;
for k=1:4
a(w,k)=el;
el=el+4;
end
end
a, % wyświetli macierz
|
PROGRAM 2 (zamieszczony poniżej) pokazuje Inną koncepcję generowania tej samej macierzy. Tutaj w pętli zewnętrznej generowane są wartości pierwszego elementu każdego wiersza (jako wartości zmiennej i), natomiast w pętli wewnętrznej - jako j - generowane są kolejne elementy wiersza zapoczątkowanego przez wartość i. Osobno - przy pomocy poleceń w=0, w=w+1 oraz k=0, k=k+1 umieszczonych w odpowiednich miejscach, generowane są indeksy elementów macierzy - które jak zawsze muszą przyjmować wartości kolejnych liczb naturalnych.
% PROGRAM 2
clear;
w=0;
for i=1:2:7
w=w+1; k=0;
for j=i:4:i+3*4
k=k+1;
a(w,k)=j;
end
end
a
|
Przykład 2:
Kolejny przykład pokazuje jak można wygenerować macierz trójkątną w której początkowe elementy wierszy są coraz mniejsze ale liczba niezerowych elementów rośnie.
W tym przypadku okazało się celowe zastosowanie innego typu pętli a mianowicie wewnętrzną pętlą jest pętla typu WHILE.
|
Wygenerować |
Przykładowy program: |
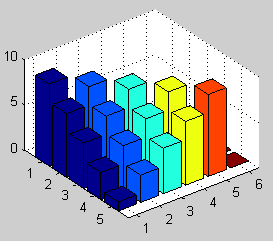
Wykres typu bar3(A) |
9 0 0 0 0 0 7 9 0 0 0 0 5 7 9 0 0 0 3 5 7 9 0 0 1 3 5 7 9 0 |
clear;
% rezerwujemy pamięć
% i zerujemy macierz:
A(4,6) = 0;
for w = 1:5
e = 11-2*w; k = 0;
while e<10
k = k+1; A(w,k) = e;
e = 2+e;
end
end
A
|
|
Do wykresów trójwymiarowych - oprócz pokazanej już funkcji bar3(A) - służą takie funkcje jak: plot3, surf, surfc, mesh, meshc. Wykresy warstwicowe pozwala uzyskać funkcja contourf. Parametrami tych wykresów są prostokątne macierze X, Y, Z zawierające poszczególne zbiory współrzędnych punktów w przestrzeni 3D.
Do przekształcenia ciągu współrzędnych x oraz y na prostokatne macierze ich wszelkich kombinacji służy funkcja [X,Y]=meshgrid(x, y)
Na przykład jeśli mamy x:
>> x=4:7
x =
4 5 6 7
|
>> y=[22.5, 23.7, 37.2] y = 22.5000 23.7000 37.2000 |
>> [X,Y]=meshgrid(x,y);
albo
>> [X,Y]=meshgrid(4:7, [22.5, 23.7, 37.2])
X =
4 5 6 7
4 5 6 7
4 5 6 7
Y =
22.5000 22.5000 22.5000 22.5000
23.7000 23.7000 23.7000 23.7000
37.2000 37.2000 37.2000 37.2000
|
Funkcja meshgrid pozwala otrzymać wykres 3D bez użycia pętli:
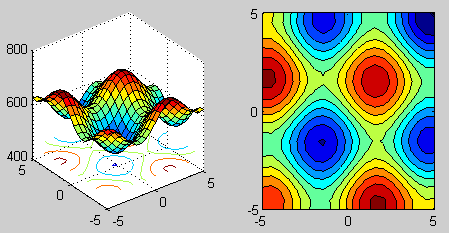
clear; clc % najpierw MACIERZE punktów (X, Y) dla wykresu 3D: [X,Y]=meshgrid(-5:0.5:5, -5:0.5:5) % następnie definiujemy macierz Z: Z = 600 -X.*Y + 50*sin(X) + 50*sin(Y); % 1) wykres powierzchniowy: subplot(1,2,1); surfc(X,Y,Z); % 1)wykres warstwicowy: subplot(1,2,2); contourf(X,Y,Z); |
|
Objaśnienia masz TUTAJ