Zacznijmy od zależności, która jest przedstawiana na pierwszej lekcji działu trygonometrii w szkole średniej. Dotyczy trójkąta prostokątnego,a dokładniej kątów ostrych. Narysujmy trójkąt prostokątny i oznaczmy jego boki oraz kąty.
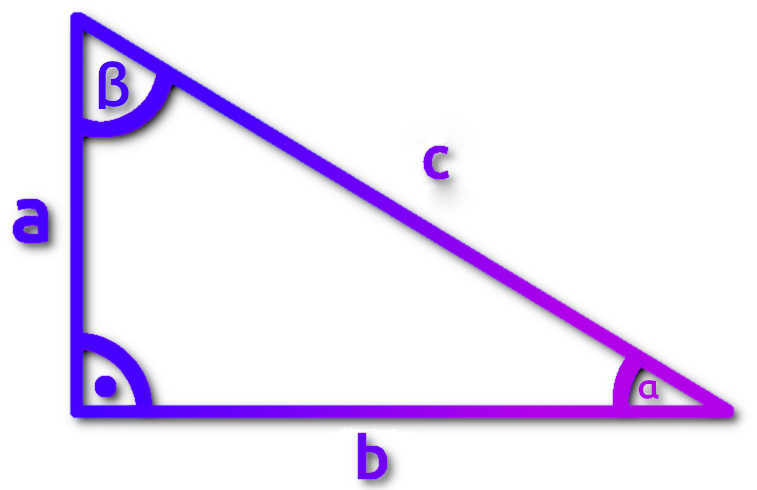
Okazuje się, że jeśli mamy podane dwie długości boków oraz trójkąt jest prostokątny, to możemy obliczyć oba kąty! Przydadzą nam się do tego funkcje sinus/cosinus/tangens. To jaką funkcję użyjemy zależy od tego które boki mamy podane. Zanim jednak zaczniemy cokolwiek liczyć, nauczmy się paru rzeczy.
Przyjrzyjmy się rysunkowi. Każdy z tych boków możemy jakoś nazwać. Skupmy się na boku c. Jest nazywany przeciwprostokątną, ponieważ leży naprzeciw kąta prostego.

Boki a i b natomiast nazywane są przyprostokątnymi, ponieważ razem łączą się tworząc kąt prosty.

Teraz przejdźmy do poznania funkcji trygonometrycznych. Zaczniemy od sinusa. Wybierzmy dowolny kąt ostry z naszego trójkąta prostokątnego. Dla przykładu wezmę kąt α. Sinus kąta α (sinα) jest równy stosunkowi długości przyprostokątnej leżącej naprzeciw kąta α do długości przeciwprostokątnej trójkąta. Z tego wynika wzór:

Nie potrafisz sobie tego wyobrazić? Napisałem krótki program, który oblicza sinusa w zależności od boków. Tak wiem, nie jest najładniejszy, ale działa. Spójrz tutaj:

Kolejną dziś poznaną funkcją będzie cosinus. Cosinus (cosα) to stosunek długości przyprostokątnej przyległej do kąta α i długości przeciwprostokątnej. Można zauważyć, że jest podobny do sinusa, tylko wykorzustujemy tę drugą przyprostokątną.
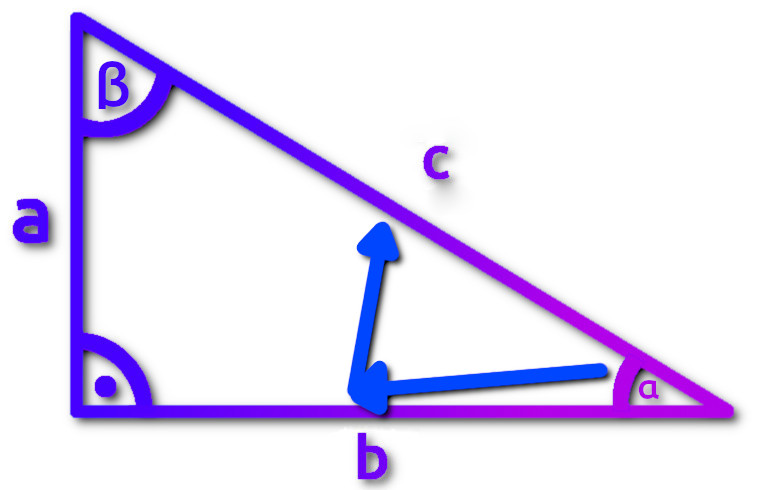
Kolejną funkcją, którą dzisiaj poznamy jest tangens. Tangensem (tgα) nazywamy stosunek długości przyprostokątnej leżącej naprzeciw kąta α do długości przyprostokątnej przyległej do kąta α.

Istnieje również funkcja zwana cotangensem (ctgα). Jest to odwrotność tangensa (1/tgα).
Oczywiście te same zależności występują dla kąta β. Dla przykładu sinβ = b/c. Co ciekawe funkcje trygonometryczne są w pewnym sensie zależne od siebie. Dla przykładu mając sinα oraz cosα jesteśmy w stanie wyliczyć tgα ze wzoru:
Ponadto mając sinusa/cosinusa jesteśmy w stanie obliczyć to drugie z tzw. jedynki trygonometrycznej!
Teoria za nami. Załóżmy, że boki powyższego trójkąta to: a = 5, c = 10. Na podstawie tych danych wyliczymy kąt α.
sinα = 5/10 = 1/2 = 0,5
Co dalej? Szukamy dla jakiego kąta sinus przyjmuje wartość 0,5. Pytanie tylko gdzie? Odpowiedź brzmi w tablicach wartości funkcji trygonometrycznych. W skrócie jest to tabela która pokazuje nam jaką wartość przyjmuje dana funkcja dla danego kąta. Przykładową tablicę można znaleźć tutaj. Korzystamy z sinusa, więc póki co obchodzi nas kolumna z sinusami. Wiemy, że nasz sinus przyjmuje wartość 0,5. Szukamy takiej wartości w naszej kolumnie. Gdy już znaleźliśmy wartość, patrzymy jaki reprezentuje kąt. W naszym przypadku α = 30o! Taki sam rezultat pokazuje program, który możesz znaleźć tutaj. (Dwukrotnie zmniejszyłem boki, ponieważ program nie pozwala aby wartość boku była większa od 8 (trójkąt wyszedłby poza płótno), ale efekt jest ten sam:

Teraz dowiemy się coś nowego na temat kątów. Na sam początek wyobraźmy sobie jakiś kąt α:
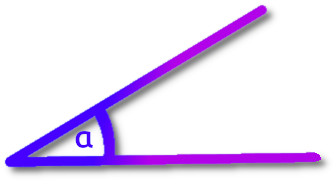
Nic niekawego. Mamy dwa ramiona tworzące kąt α. Teraz poznamy kąt skierowany. Jest to kąt spełniający dane warunki:
✓ Jest to kąt płaski
✓ Ma ustalone uporządkowanie ramion
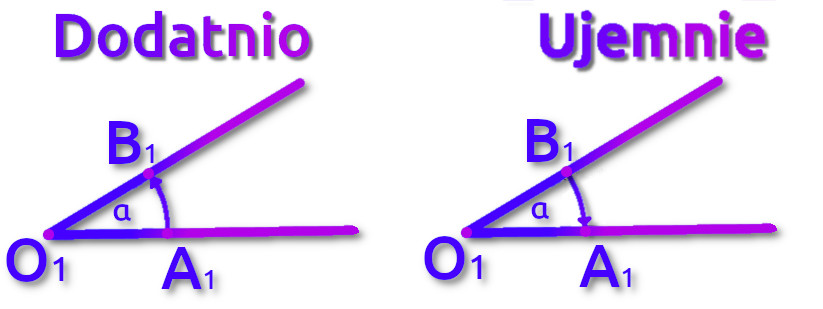
Co ciekawe, jego ramiona nazywają się różnie. Pierwsze ramię będziemy nazywać ramieniem początkowym, a drugie ramieniem końcowym. Teraz pokażę dwa przykłady kątów skierowanych:

Jak się pewnie domyślasz proste O
Teraz umieścimy kąt w układzie współrzędnych. Aby to zrobić musimy spełnić pewne warunki:
✓ Wierzchołek kąta musi znajdować się w punkcie (0,0) układu współrzędnych
✓ Ramię początkowe musi pokrywać się z dodatnią cześcią osi X
Tak wygląda kąt α w układzie współrzędnych:
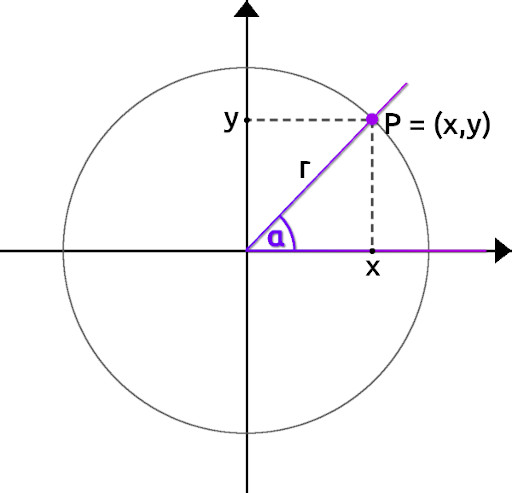
Jak możemy zauważyć, dla kąta α możemy obliczyć funkcje trygonometryczne. Będą one wyglądały następująco:
cosα = x/r
tgα = y/x
ctgα = x/y
Dla przykładu wyliczymy teraz sinα, dla x = 3; y = 4. Z twierdzenia Pitagorasa r = 5. Wtedy:

W naszym przypadku gdzie x = -3 i y = 4, sinα również wynosi 4/5. Powiększmy wartość kąta α jeszcze trochę:

Jeżeli w tym przypadku podstawimy te same liczby, czyli x = -3 i y = 4 to sinα = -4/5! Co z tego wynika? Każda funkcja trygonometryczna jest dodatnia lub ujemna w różnych ćwiartkach. Jeżeli każdą z 4 poznanych dotąd funkcji policzylibyśmy tak samo jak sinusa, to funkcje byłyby dodatnie w następujących ćwiartkach:
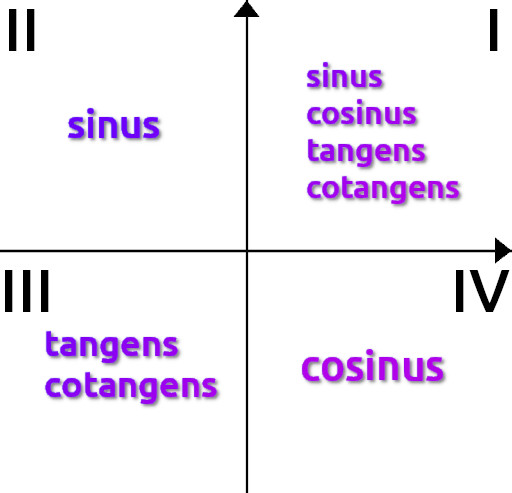
Niektórym jest to łatwiej zapamiętać w takiej formie:
I: wszystkie
II: sinus
III: tangens | cotangens
IV: cosinus
Jednak kąt może być większy od 360o. Co robić w takim przypadku? Zacznijmy od rysunku.

Można zauważyć, że ramię końcowe kąta α jest w tym samym miejscu co ramię końcowe kąta β . W tym przypadku będzie nam dobrze skorzystać z tzw. wzorów redukcyjnych. Pozwolą one zapisać nam kąt α tak, aby 90o> α > 0o. Wtedy będzie nam łatwo odczytać wartości funkcji trygonometrycznych (tabela pokazuje wartości od 0o to 90o). Jak to zrobić?
✓ Kąt α przedstawiamy w postaci 90o +- β, 180o +- β, 270o +- β, 360o +- β
✓ Ustalamy jaki znak ma wartość funkcji trygonometrycznej w danej ćwiartce na podstawie kąta α.
✓ Jeżeli przed +- β występuje wielokrotność 180o, to rodzaj funkcji się nie zmienia.
✓ Jeżeli przed +- β występuje wielokrotność 90o nie będąca wielokrotnością 180o, to funkcję zamieniamy na kofunkcję (sinus na cosinus, tangens na cotangens i na odwrót)
Przykład na podstawie powyższego rysunku. Załóżmy, że α = 390o, a β = 30o i chcemy obliczyć sinusa. Postępujemy tak jak podano powyżej:
✓ α = 360o + 30o
✓ Jak widać na powyższym obrazku ramię końcowe kąta 390o znajduje się w pierwszej ćwiartce, gdzie wszystkie funkcje są dodanie.
✓ Przed + 30o występuje wielokrotność 180o, więc sinus pozostaje bez zmian. Jeżeli przed + 30o mielibyśmy np 90o to nasz sinα musielibyśmy zamienić na cosα.
✓ Ostatecznie sin390o = sin(360o + 30o) = sin30o = 0,5!
Wkrótce zaczniemy rysować funkcje trygonometryczne na wykresie. Zanim to jednak nastąpi, dobrze byłoby poznać jeszcze jedną rzecz, aby było nam wygodniej rysować wykresy. Dotąd kąty określaliśmy za pomocą stopni. Kąt możemy również zapisać za pomocą radianów/miary łukowej kąta. Jest to stosunek długości łuku okręgu na którym jest oparty dany kąt, do długości promienia r tego okręgu, więc wynika z tego wzór:
Na poniższym gifie widać jak miara łukowa ma się do kątów:
Z powyższej animacji można wywnioskować, że dla 360o miara łukowa wynosi 2π, 180o = π, 90o = π/2 itd.
Z tego wynika, że 1o to π/180o rad, a 1 rad to 180o/π. Ktoś może się zapytać po co to wiedzieć? Wyobraźmy sobie sytuację, że rysujemy funkcje f(x) = sin(x). Im większy x, tym większy kąt jaki obliczamy. Na dłuższą metę podpisywanie osi x wartościami rzędu 1440o, 2160o itd byłoby męczące. Dzięki radianom (mierze łukowej kąta) takie liczby mozemy zapisać jako: 8π oraz 12π.
Popatrzmy się jeszcze raz na powyższego gifa. Tym razem skupmy się na wartości funkcji sinus i cosinus dla danego kąta:
Wraz ze wzrostem kąta α nasze funkcje sinus i cosinus oscylują między 1 a -1. Jeżeli mielibyśmy narysować fukcję sin(x) (sinusoidę) tak jak każdą inną, wyglądałoby to tak:

Gdybyśmy kontynuowali w nieskończoność, to wykres cały czas byłby falą (możesz to sprawdzić tutaj). Z powyższego gifa możemy wyciągnąć kilka informacji. Okres funkcji wynosi 2π (2π to 360o po których funkcja znowu się "powtarza"). Widać również miejsca zerowe równe: π i 2π. Jednak wcześniej wspomniałem, że funkcja ta ciągnie się w nieskończoność. Jeżeli ktoś poprosi nas o wypisanie miejsc zerowych dla liczb rzeczywistych, to co mamy zrobić? Zauważmy, że odległość między sąsiednimi miejscami zerowymi jest taka sama i wynosi π. Pierwsze miejsce zerowe jest równe 0, więc 0 · π = 0. Drugie jest równe 1 · π = 1π, trzecie 2 · π = 2π, czwarte 3 · π = 3π itd. Zauważmy, że funkcja sinus występuje również dla kątów skierowanych ujemnie (x < 0), więc miejsce zerowe również znajduje się w -π. Wzór na miejsca zerowe funkcji f(x) = sin(x) wynosi:
Jeżeli ciężko jest ci to sobie wyobrazić, to odsyłam do programu rysującego funkcje, ponieważ pokazuje również miejsca zerowe danej funkcji i nie tylko (Kliknij tutaj). Dla przykładu wykres funkcji f(x) = sin(x):

Drugą funkcją trygonometryczną będzie cosinusoida. Ponownie przypatrzmy się tej animacji, tym razem zwracając uwagę na wartość cosinusa:

Poniższa animacja pokazuje tworzącą się cosinusoidę. Jak widać nie jest to tak instynktowne jak wcześniejszy przypadek:

Można się jednak doszukać pewnych podobieństw cosinusoidy z sinusoidą (zbiór wartości, okres podstawowy, monotoniczność przedziałami itp.). Co więcej, wkrótce poznasz wzory redukcyjne. Na ich podstawie można wywnioskować, że wykresy funkcji cosinus i sinus przesunięty o 90o w lewo się na siebie nakładają. Tak wygląda porównanie:

Podobnie jak w przypadku sinusoidy, funkcja ma miejsca zerowe, monotoniczność, zbiór wartości, okres podstawowy i inne własności. Poniższe zdjęcie demonstruje przykładowe własności funkcji cos x:

Ostatnią funkcją na której się skupimy jest tangensoida. Różni się trochę od wcześniej poznanych wykresów, bowiem tangensoida ma pewne proste do których zmierza, ale nigdy ich nie osiąga. Nazywamy je asymptotami. Dlaczego tak jest? Mam nadzieję, że pamiętasz, iż tangensa można było wyliczyć ze wzoru:
Liczba w mianowniku (cosα) nie może być zerem. Dla jakich wartości cosα jest równe 0? Dla π/2, 3π/2, π/2 + kπ. Dla tych wartości narysujemy asymptoty w postaci przerywanych linii prostych. Tak będzie wyglądał wykres funkcji f(x) = tg(x):

W powyższym przykładzie asymptoty są zaznaczone na żółto, jednak w programie do rysowania funkcji trygonometrycznych widzimy je jako linie proste o szarym kolorze. Tym razem zbiór wartości funkcji nie ogranicza się do 1, bądź -1 (dąży do +-∞). Chciałbym zaznaczyć, iż tangensoidę również można rysować w nieskończoność. Za przykład niech posłuży wykres funkcji tg(x) z programu do rysowania funkcji:

Źródła merytoryczne:
- https://teoriaelektryki.pl/zrozumiec-sinusoide/
- https://www.matemaks.pl
- https://www.youtube.com/watch?v=ovLbCvq7FNA
- Matematyka poznać, zrozumieć cz 1/2 - WSiP
- Teraz matura vademecum - Nowa Era
- Matematyka - Podręcznik do liceów i techników klasa 1. - OE




