
Częstotliwość tej sinusoidy moglibyśmy nazwać tętnem. Kardiomonitor, czyli urządzenie, które monituruje procesy życiowe prezentuje dane najczęściej w formie wykresów, gdzie króluje sinusoida. Kolejnym ciekawym przykładem jest dźwięk. Funkcja sinus/cosinus może być traktowana jako graficzna reprezentacja dźwięku. Tak wygląda graficzna wizualizacja dźwięku w programie Audacity:

Jak widać jest to "zlepek" sinusoid o różnym okresie i amplitudzie. Im większa częstotliwość sinusoidy (odwrotność okresu) tym niższy dźwięk. Im mniejsza wartość maksymalna sinusoidy tym dźwięk będzie cichszy. Graficznie możemy to przedstawić następująco:
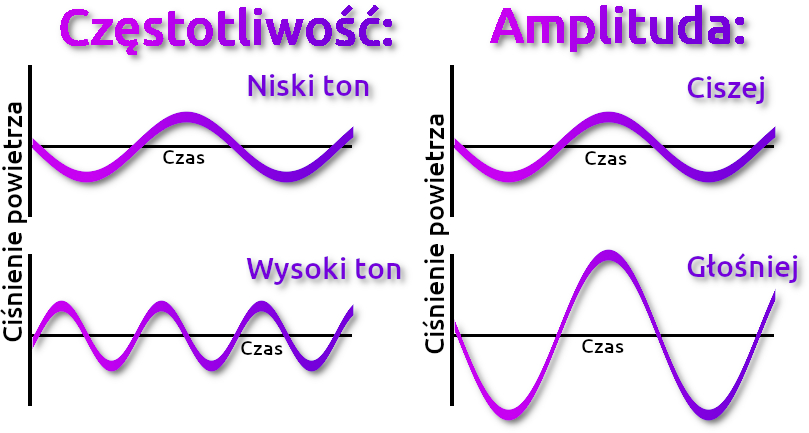
Dzięki takiej interpretacji dźwięku przez komputer, inżynierowie są w stanie manipulować dźwiękiem wedle potrzeb (np. zniekształcając dźwięk w grach na podstawie pozycji gracza, by pogłębić realizm wykreowanego świata). Skoro już jesteśmy przy sinusoidach, to prąd dostarczany do naszych gniazdek ma charakter sinusoidalny. Prąd ten raz płynie w jedną, a raz w drugą stronę tylko na chwilę osiągając wartość maksymalną. Dlaczego tak jest? Transport prądu przemiennego jest znacznie tańszy od prądu stałego. Ponadto maszyny generujące prąd przemienny są prostsze w konstrukcji.
Kolejnym niesamowicie ciekawym działem, w którym czerpie się z trygonometrii są gry komputerowe. Trygonometria stosowana jest tam w naprawdę wielu miejscach. Oczywiście, aby nie być gołosłownym podam parę przykładów. Zaczniemy od animacji. Są one jednym z fundamentów gier komputerowych. Proszę spojrzeć na przykład na tego gifa:

Sinusoida jest w tym przypadku odpowiedzialna za przechowywanie pozycji modelu monety w czasie, tak, aby poruszała się w górę i w dół. Z racji tego, że sinusoida jest funkcją ciągnącą się w nieskończoność, to animacja będzie płynnie trwała przez cały czas gry. Z takich oto sinusoid składają się animacje w grach. Oczywiście podobnie jak w przypadku cyfrowego dźwięku są najczęściej połączeniem sinusoid o różnych parametrach. Kolejnym przykładem, już nie związanym z wykresami funkcji jest obliczanie kierunku na podstawie kąta. Kiedy się to może przydać? Prosty przykład. Załóżmy, że tworzymy grę 2D. Gracz to zielona kulka, a ściany są czerwone. Wyglądałoby to tak:

Chcemy, aby gracz nie widział tego co znajduje się za ścianami. Chcemy zwizualizować jego pole widzenia. Przydaje się to w grach często nawet po to, aby zrobić cienie obiektu (byłaby to odwrotność pola widzenia). Jeden ze sposobów aby to zrobić wymaga użycia funkcji trygonometrycznych. Dookoła gracza wystrzelimy kilkaset promieni (pomijam optymalizację) sprawdzających gdzie znajdują się przeszkody. Zaczniemy pierwszy strzał powiedzmy w kącie 0o i kąt każdego następnego promienia będzie o jeden stopień większy. Teraz potrzebujemy obliczyć kierunek promienia (wektor) na podstawie kąta. Zwróćmy uwagę na fakt iż pozycję gracza możemy potraktować jako środek okręgu. Narysujmy to wraz z jakimś przykłądowym promieniem.

Jeżeli wyliczymy sinusa 30o to otrzymamy dokładną wartość x. Współrzędną y możemy obliczyć funckją cos30o. Taką operację uczynimy dla każdego promienia. Wszystkie wystrzelone promienie będą wyglądały tak:
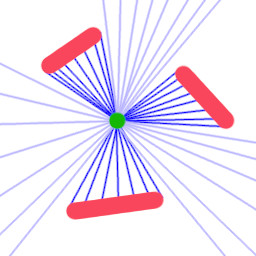
Znając informację o punktach w których znajdują się obiekty, możemy wygenerować teksturę wizualizującą pole widzenia gracza, bądź cień:


Te przykłady są oczywiście kroplą w morzu. Chciałem abyś zrozumiał/ała mniej więcej po co jest to potrzebne w grach. Trygonometrię można użyć też np w:
- Obliczaniu kierunku obiektów po ich zderzeniu
- Obracaniu obiektu
- Obliczania trajektorii lotu obiektu
i wielu innych przypadkach!
Póki co nie skupiliśmy się na trygonometrii sferycznej, a jest to temat przewodni strony. Jednym z przykładów jest astronomia. W niej bowiem geometria/trygonometria sferyczna jest wręcz fundamentem. Dzięki temu astrologowie są w stanie obliczyć szerokości geograficzne, wschody i zachody ciał niebieskich, czas gwiazdowy i wiele innych co do sekundy! Nie musimy też ograniczać się do ziemii. Dzięki trygonometrii naukowcy są w stanie obliczyć trajektorię lotu satelit, oraz z jaką siłą trzeba wystrzelić obiekt, aby trafił na stabilną orbitę!

Niestety zadania związane z astronomią wymagają również znajomości sferycznego układu współrzędnych, więc podawanie przykładu niemożliwego do zrozumienia nie ma sensu. Trygonometria sferyczna znalazła również zastosowania w nawigacji (najczęściej dla samolotów). Możemy rozwiązać jeden z prostszych przykładów wykorzystania trygonometrii sferycznej. Wyobraźmy sobie, że znajdujemy się na równiku. Naszym zadaniem jest dostać się do punktu D. Wiemy, że odległość tego punktu od równika wynosi 60o, oraz, że odległość między punktem w którym stoimy, a punktem A (patrz rysunek) wynosi 30o. Naszym zadaniem jest obliczyć odległość między miejscem w którym stoimy a docelowym.
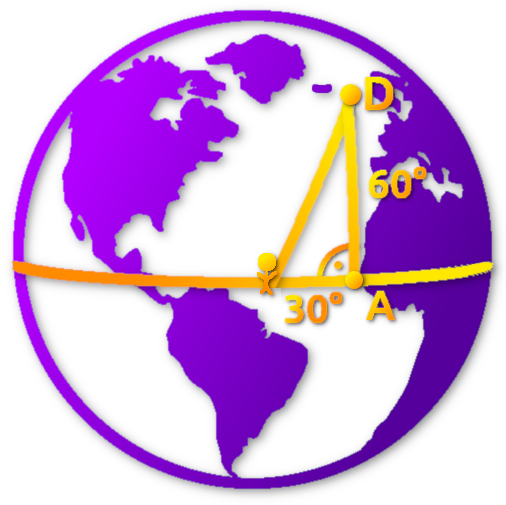
Cała trudność zadania polega na wyliczeniu przeciwprostokątnej z twierdzenia Pitagorasa:
cos a = cos b * cos c
Po podstawieniu kątów do b i c, szukana odległość wyniesie około 64o. Teraz stopnie musimy zamienić na fizyczną odległość. Wystarczy obwód Ziemi pomnożyć przez 64o/360o. Po dokonaniu tej kalkulacji dowiemy się, że odległość wynosi około 7 111 km (przy założeniu, że obwód Ziemi to 40 tys km.).
Jeżeli ktoś dalej nie jest przekonany, dlaczego jest to tak bardzo ważne zagadnienie, spieszę z kolejnym przykładem. Załóżmy, że chcemy dotrzeć do Nowego Jorku z Warszawy. Oczywiście najszybszym środkiem transportu będzie samolot. Naszym zadaniem jest narysować najkrótszą drogę między tymi miastami. Każdy instynktownie narysowałby coś takiego (Tu i niżej korzystałem z Map Google):

Odpowiedź byłaby poprawna, gdyby nie fakt, że Ziemia jest kulistego kształtu. Prawdziwa odpowiedź wygląda tak:

Oczywiście przy mniejszych skalach (Na przykład z jednego polskiego miasta do drugiego) taka precyzja jest niepotrzebna, dlatego odległość liczymy po linii prostej. Jeżeli zrozumieliśmy dlaczego tak się dzieje, to pora na zadanie.

Musimy obliczyć (tym razem co do minuty), jaka jest najkrótsza droga między Londynem, a Nowym Jorkiem. Zacznijmy od tego, że Nowy Jork jest położony na kole wielkim o długości geograficznej 74o0'W i w przybliżeniu 40o42' szerokości geograficznej równika. Jeżeli od 90o odejmiemy 40o42', to otrzymamy odległość od bieguna północnego równą 49o18'. Podobną kalkulację zrobimy dla Londynu. Położony jest bowiem wzdłuż koła wielkiego o długości geograficznej równej 0o5'W oraz o około 51o32' na północ od równika. Po odjęciu tej wartości od 90o otrzymujemy 38o28'. Boki b i c są długościami łuków od Bieguna Północnego do odpowiednio Nowego Jorku, oraz Londynu, więc b = 49o18', oraz c = 38o28'. Kąt A jest dany przez różnicę w południkach długości geograficznych obu miast, więc A = 74o0' - 0o5'W = 73o55'. Korzystając ze wzoru na cosinus boku, o którym mowa była tutaj otrzymamy:
cos a = (0.6521 · 0.7830) + (0.7581 · 0.6221 · 0.2770)
cos a = 0.6412
a = 50.1186o lub 50o7'
Źródła wiedzy:
- https://vesta.astro.amu.edu.pl/Staff/Iwona/geograf.pdf
- http://www.siranah.de/html/sail042e.htm
- https://spheresandsuch.wordpress.com/2011/03/11/how-do-people-use-spherical-geometry/
- http://www.math.ubc.ca/~cass/courses/m308-02b/projects/franco/index.htm
- Reszta jest stworzona przezemnie na podstawie własnych spostrzeżeń i doświadczeń




