Przekształcenia , które wykorzystuję do generowania matematycznych gór to tzw. przekształcenia afiniczne, które punktom płaszczyzny przyporządkowują inne punkty płaszczyzny. Jeśli jest dowolnym punktem płaszczyzny, to
. Dla przykładu rozpatrzmy przekształcenie . Dla dostaniemy . Mówiąc precyzyjniej, obrazem punktu jest punkt .
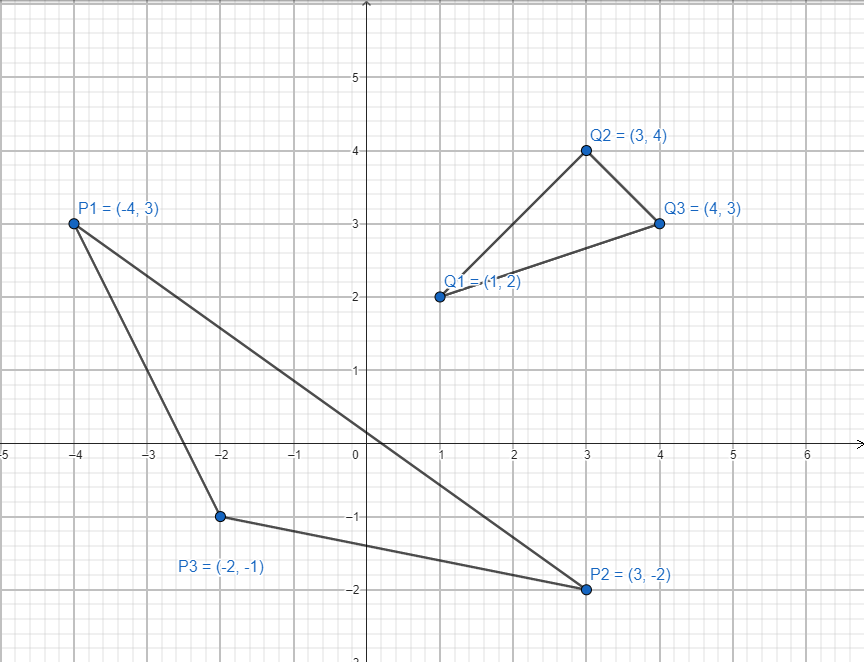
Okazuje się, że mając dane na płaszyźnie dwa trójkąty pierwszy o wierzchołkach drugi o wierzchołkach (punkty nie mogą być współliniowe) to zawsze możemy znaleźć odwzorowanie afiniczne odwzorowujące jeden z nich na drugi. Wystarczy rozwiązać układ sześciu równań z sześcioma niewiadomymi: Jeśli boki trójkąta przekształcanego będą krósze od odpowiednich boków jego obrazu, to możemy twierdzić, że przekształcenie jest zwężające. Dla przykładu obliczę współczynniki przekształcenia afinicznego , które odwzorowuje trójkąt o wierzchołkach na trójkąt o wierzchołkach . Trójkąty przedstawiłem na obrazie obok.
Należy w tym celu rozwiązać następujący układ równań: Rozwiązaniami układu są liczby: Odwzorowanie wygląda zatem następująco:
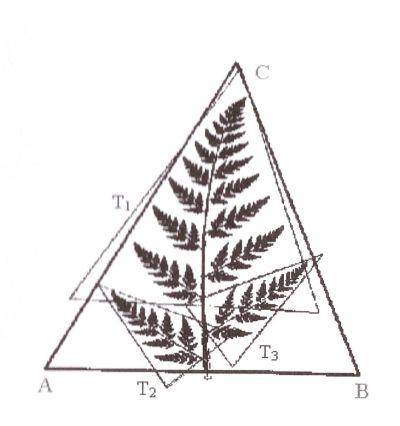
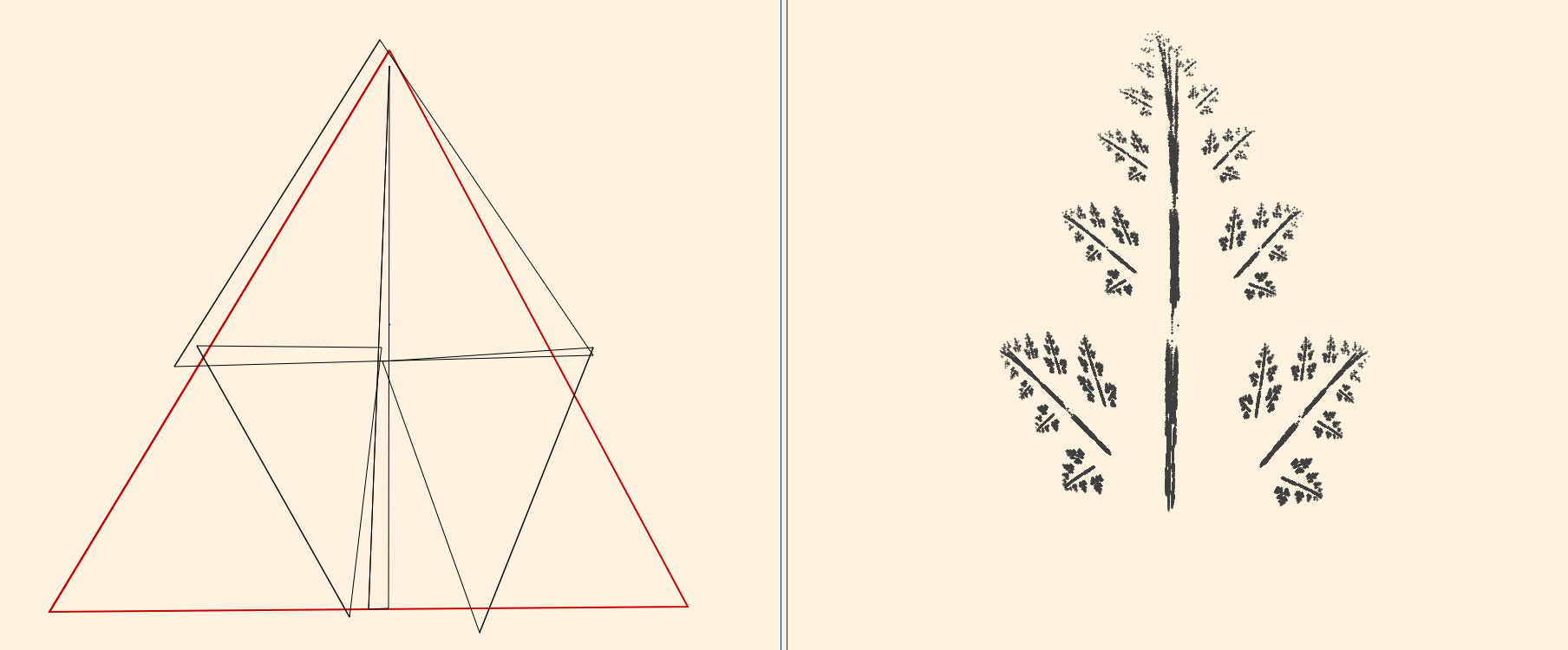
Okazuje się, że jeśli mamy n odwzorowań zwężających, np. takich które były rozważane powyżej to odwzorowanie jest również przekształceniem zwężającym. Odwzorowanie to nosi nazwę odwzorowania Hutchinsona.
. Dla przykładu rozpatrzmy przekształcenie . Dla dostaniemy . Mówiąc precyzyjniej, obrazem punktu jest punkt .
Okazuje się, że mając dane na płaszyźnie dwa trójkąty pierwszy o wierzchołkach drugi o wierzchołkach (punkty nie mogą być współliniowe) to zawsze możemy znaleźć odwzorowanie afiniczne odwzorowujące jeden z nich na drugi. Wystarczy rozwiązać układ sześciu równań z sześcioma niewiadomymi: Jeśli boki trójkąta przekształcanego będą krósze od odpowiednich boków jego obrazu, to możemy twierdzić, że przekształcenie jest zwężające. Dla przykładu obliczę współczynniki przekształcenia afinicznego , które odwzorowuje trójkąt o wierzchołkach na trójkąt o wierzchołkach . Trójkąty przedstawiłem na obrazie obok.
Należy w tym celu rozwiązać następujący układ równań: Rozwiązaniami układu są liczby: Odwzorowanie wygląda zatem następująco:
Okazuje się, że jeśli mamy n odwzorowań zwężających, np. takich które były rozważane powyżej to odwzorowanie jest również przekształceniem zwężającym. Odwzorowanie to nosi nazwę odwzorowania Hutchinsona.