spis treści
- co nazywamy elipsą?
- konstrukcja elipsy przy pomocy sznurka
- elipsa w astronomii
- własności optyczne i akustyczne elipsy
- elipsa przez spłaszczenie koła
- elipsa jako obwiednia prostych
- konstrukcja elipsy przez ślizganie odcinka
- tworzenie elipsy przez zaginanie się kartki
- elipsa jako cień kuli
- złota elipsa
- sfery Dandelina
- elipsa jako miejsce geometryczne środków okręgów
co nazywamy elipsą?
Elipsa jest miejscem geometrycznym płaszczyzny, dla których suma odległości od dwóch ustalonych punktów (ognisk elipsy) jest zawsze taka sama i równa wielkiej osi elipsy. Na wielkiej osi elipsy znajdują się jej ogniska F1 i F2.
konstrukcja elipsy przy pomocy sznurka
Powyższa definicja umożliwia skonstruować elipsę przy pomocy sznurka zaczepionego swymi końcami w dwóch stałych punktach, które będą ogniskami elipsy.
Wykorzystując podobne podejście możemy wykreślić elipsę na komputerze.
- Na odcinku AB (odpowiednik sznurka) obieramy punkt P, którego położenie będziemy zmieniać.
- Z punktów F1 i F2 wykreślamy okręgi o promieniach AP i PB.
- Punkty przecięcia tych okręgów wykreślają elipsę.
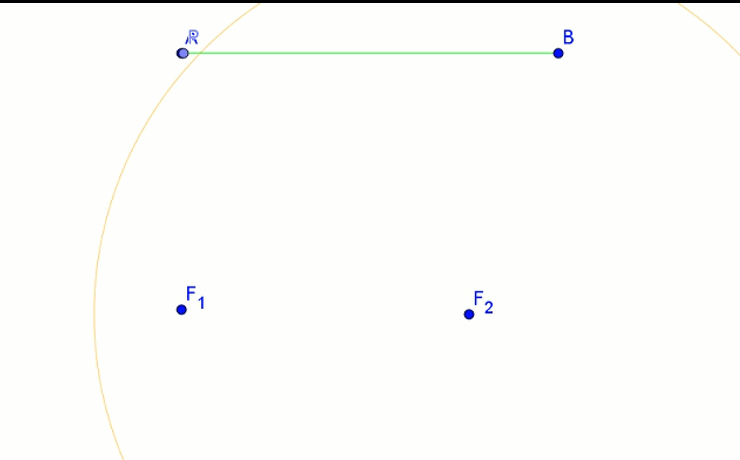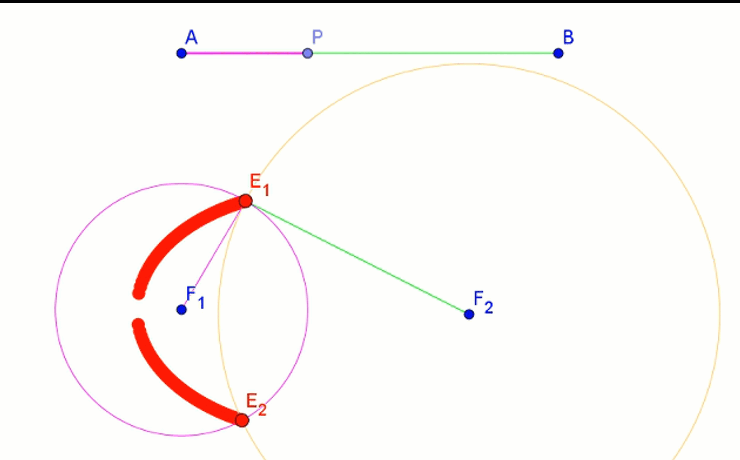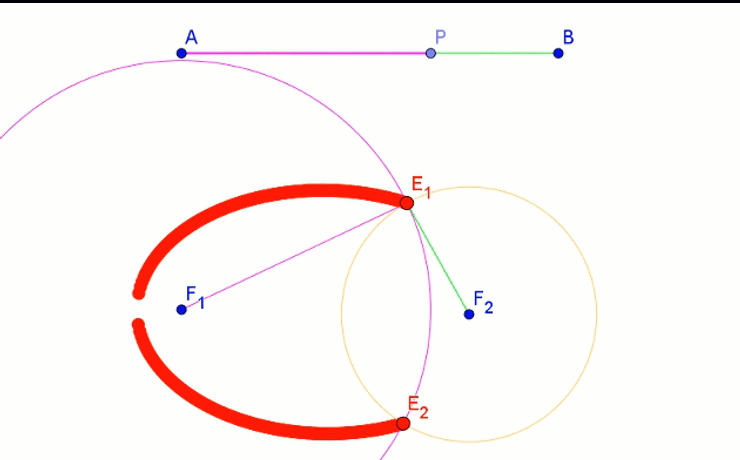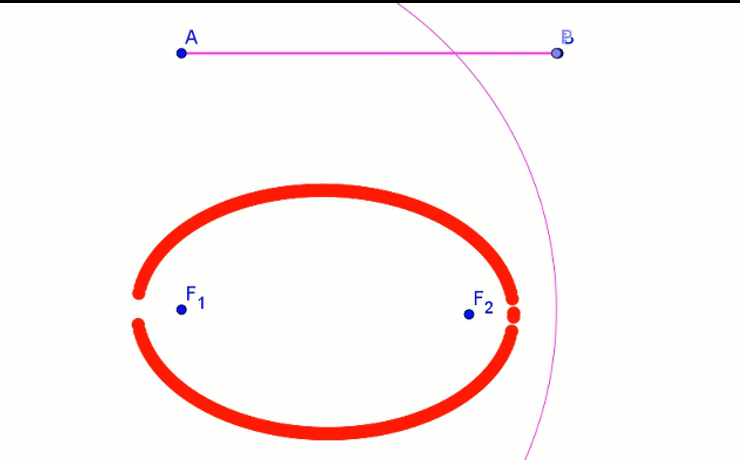
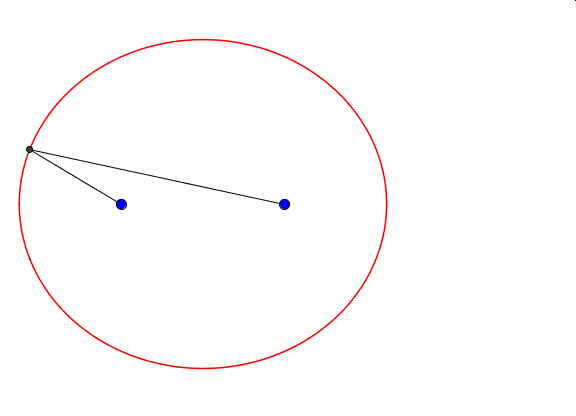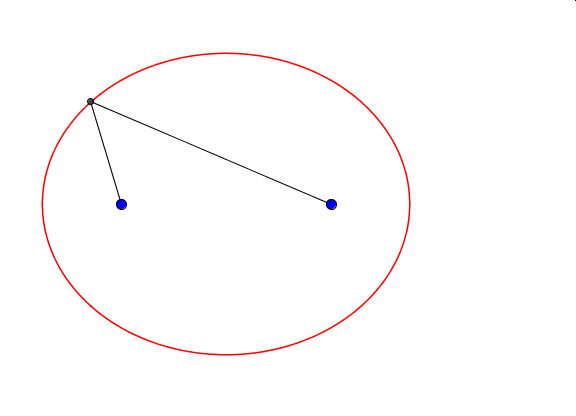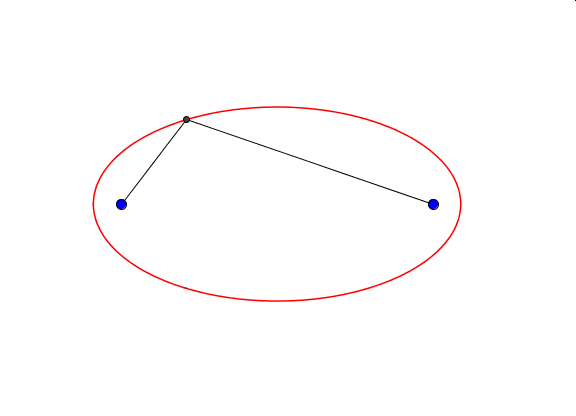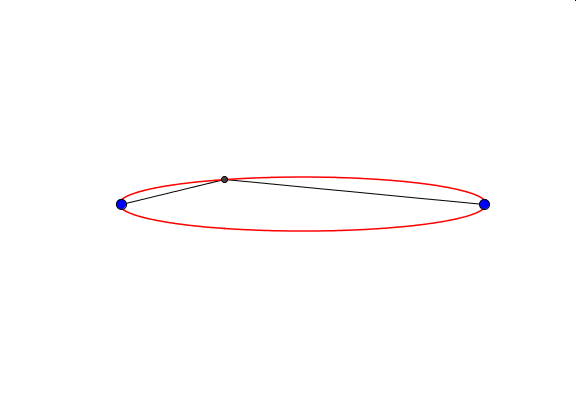
Okazuje się, że kształt i wielkość elipsy zależy nie tylko od długości sznurka, ale również od położenia jej ognisk. Długość sznurka to długość wielkiej osi elipsy. Gdy ogniska elipsy oddalają się maleje długość jej małej osi.
elipsa w astronomii
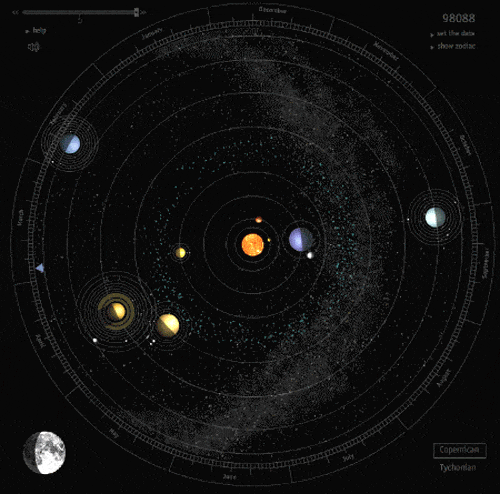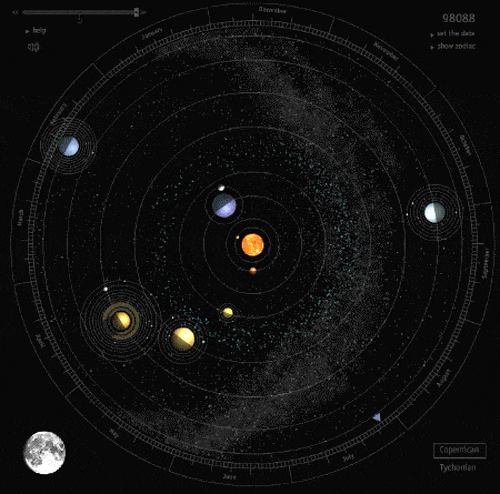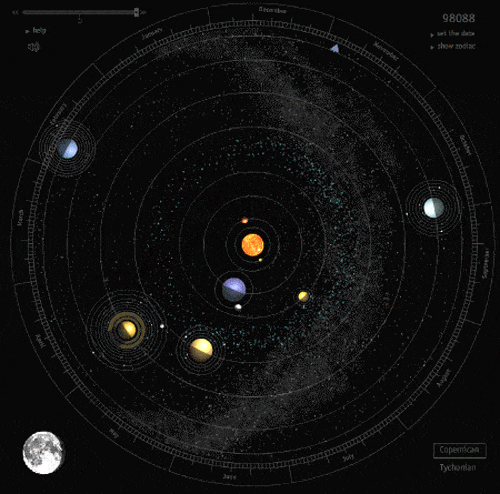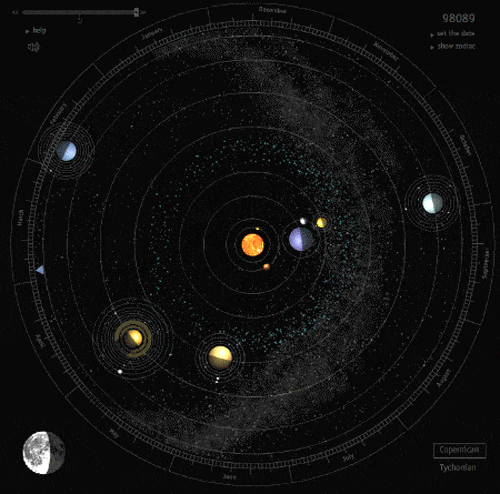
Elipsa zyskała na wartości przy okazji odkryć Jana Keplera w XVII. Sformułował on prawa dotyczące ruchu planet. Jedno z nich, pierwsze prawo Keplera mówi o sposobie poruszania się planet. Każda planeta Układu Słonecznego porusza się wokół słońca po orbicie w kształcie elipsy, w której jednym z ognisk jest Słońce.
W dzisiejszym odniesieniu prawo to zostało uogólnione i dotyczy nie tylko Układu Słonecznego, a tory ruchu nie dotyczą tylko elipsy, ale też paraboli oraz hiperboli.
własności optyczne i akustyczne elipsy
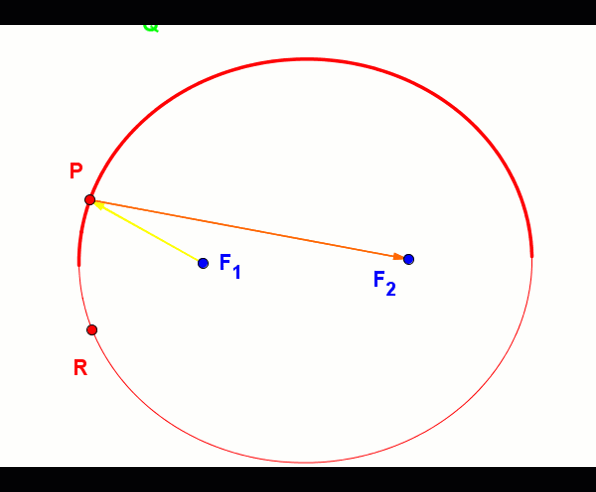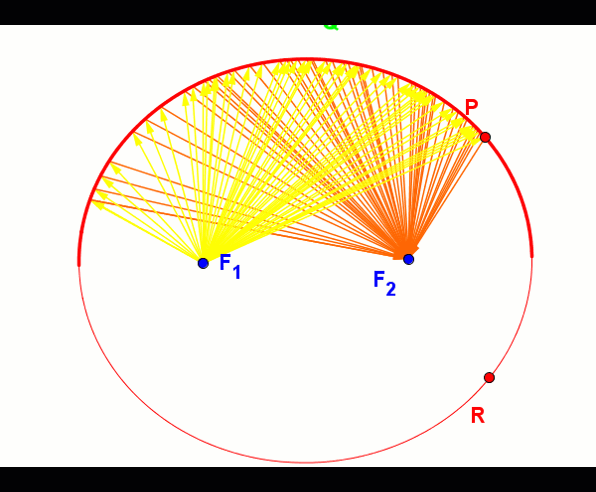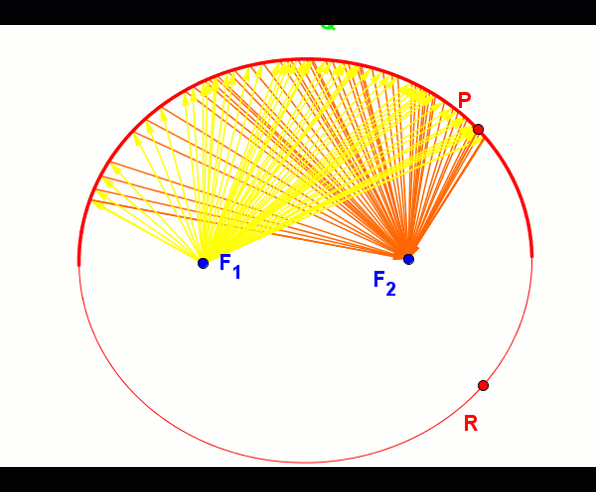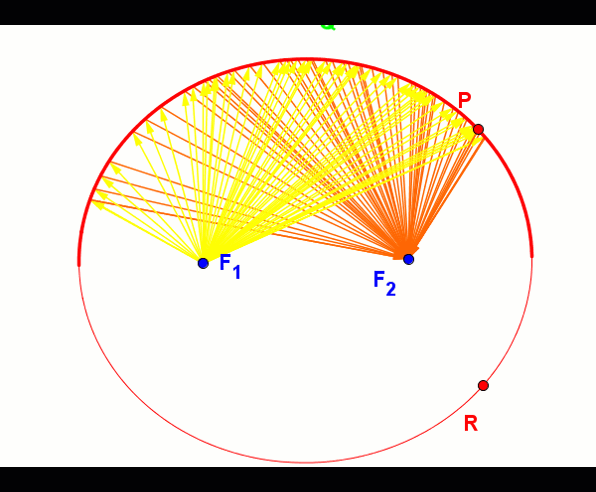
Elipsa posiada własność polegającą na tym, iż każda fala świetlna lub głosowa wychodząca z jednego z ognisk odbita od jej krawędzi wędruje przez drugie ognisko.
Zauważono to już w Starożytności. W powieści Bolesława Prusa Faraon możemy przeczytać o podstępie kapłanów egipskich, którzy wykorzystali własności dźwiękowe elipsy, aby skłócić lud egipski przeciw faraonowi Ramzesowi XIII. Sklepienie świątyni egipskiej miało przekrój eliptyczny. Jeden z kapłanów szeptał słowa Ludu, jak mnie nie wysłuchasz, to smok połknie Słońce
. Głos po odbiciu znalazł się w drugim ognisku, w którym znajdowali się fellachowie egipscy, dla których Słońce było źródłem życia. Wierząc w słowa kapłana, sądząc, że to ich bóg Ra, sprzeniewierzyli się swojemu faraonowi. To chyba jedyny przypadek w historii, kiedy obiekt matematyczny posłużył polityce...
elipsa przez spłaszczenie koła
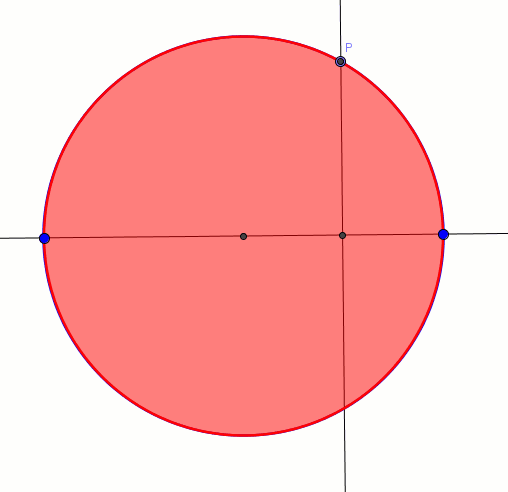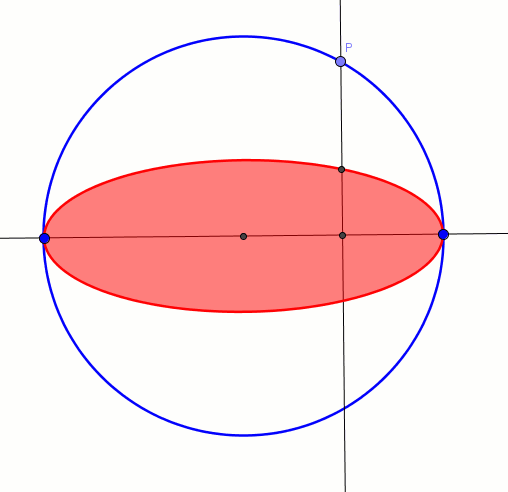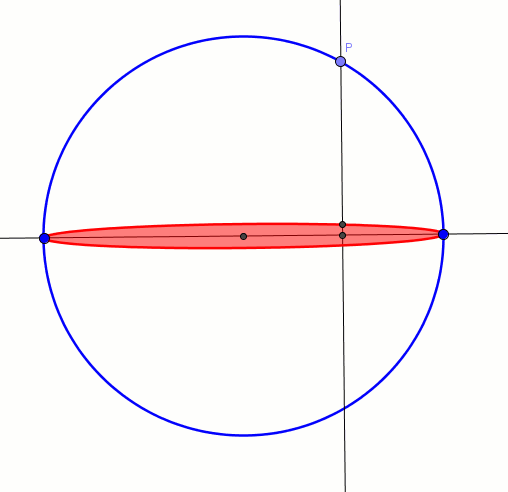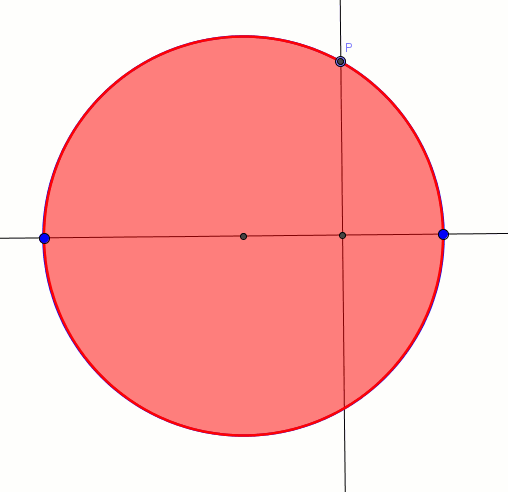
Jednym ze sposobów uzyskania elipsy jest przekształcenie każdego punktu okręgu w tzw. powinowactwie prostokątnym. Poniższa animacja prezentuje ten sposób. Okrąg (koło) przekształca się w elipsę. Skala powinowactwa prostokątnego wyraża się ilorazem długości małej osi elipsy do promienia okręgu. Gdy skala jest równa zeru, elipsa staje się odcinkiem. Na animację możemy spojrzeć też w sposób trójwymiarowy, gdzie elipsa jest rzutem koła.
elipsa jako obwiednia prostych
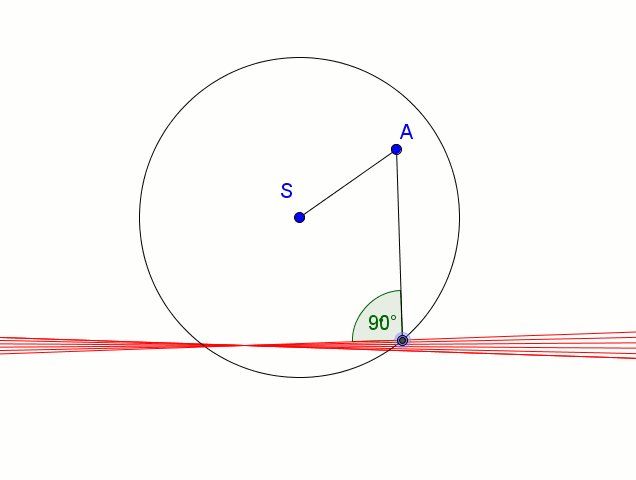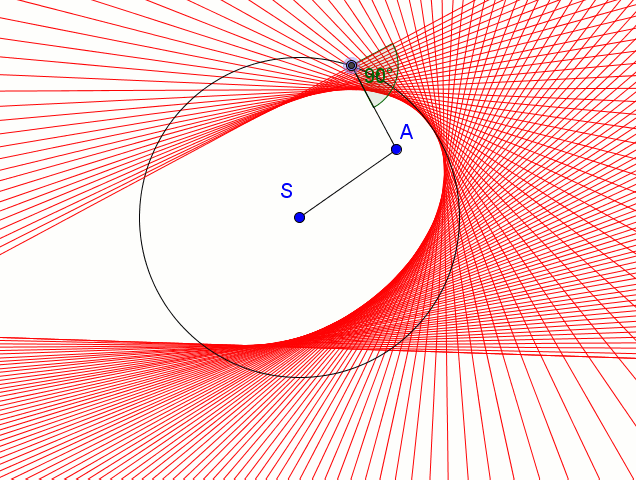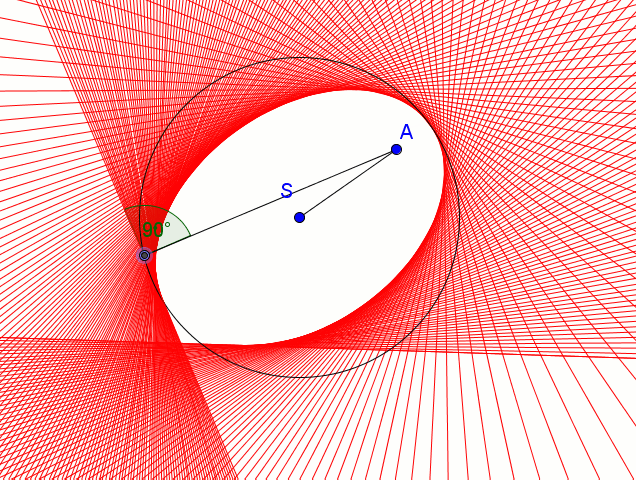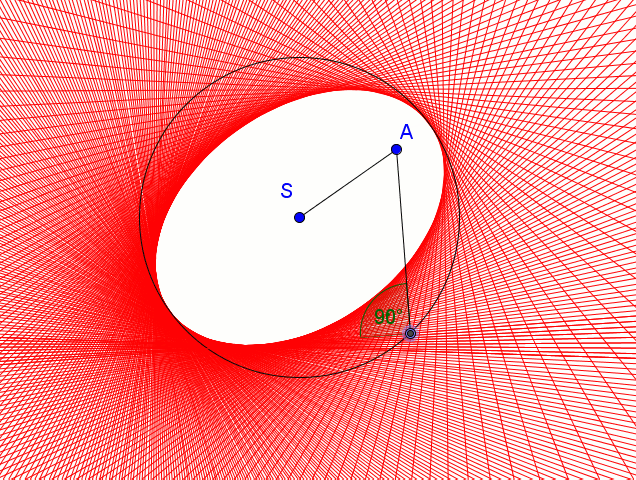
Mówimy, że krzywa jest obwiednią prostych (lub okręgów), jeśli dla każdego punktu tej krzywej istnieje jedna z prostych styczna w tym punkcie do krzywej. By uzyskać elipsę jako obwiednie prostych:
- ustalamy punkt A wewnątrz koła
- wybieramy punkt P okręgu,
- tworzymy odcinek AP,
- w punkt P kreślimy prostą prostopadłą do AP
Prosta ta w trakcie poruszania punktem P ogranicza elipsę - elipsa ta jest obwiednią rodziny tych prostych.
konstrukcja elipsy przez ślizganie się odcinka
Z pomocą specjalnego narzędzia zwanego cyrklem eliptycznym możemy konstruować elipsy. W kartezjańskim układzie współrzędnych wykonamy konstrukcję, która będzie działać na zasadzie tego właśnie urządzenia. Skonstruujemy odcinek, którego końce leżą na dodatnich półosiach układu współrzędnych w punktach A i B. Następnie obieramy punkt P na odcinku AB. Okazuje się, że podczas poruszania odcinkiem AB po osiach układu punkt P zakreśla elipsę. Jeśli punkt P umieścimy w równych odstępach od punktu A i punktu B, czyli na symetralnej odcinka AB nasza konstrukcja zakreśli okrąg. Cyrkiel eliptyczny zwany też elipsografem lub cyrklem owalnym był prawdopodobnie znany już w starożytnej Grecji.
tworzenie elipsy przez zaginanie kartki
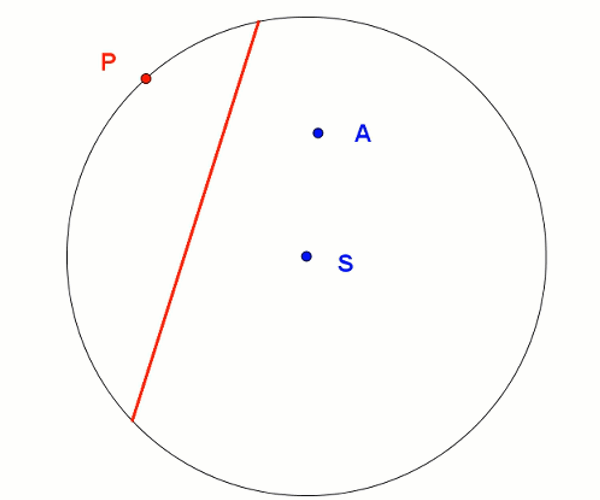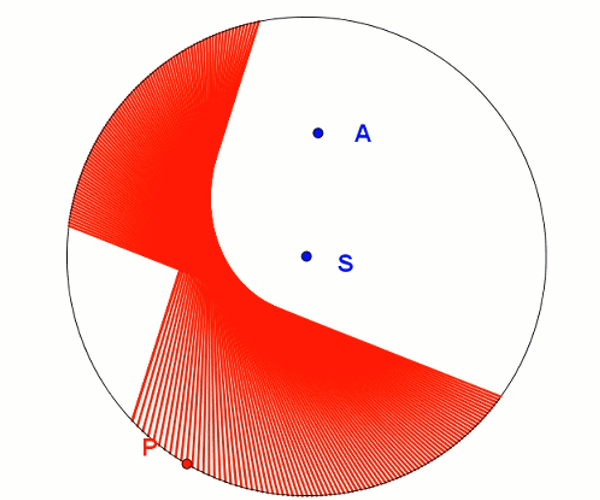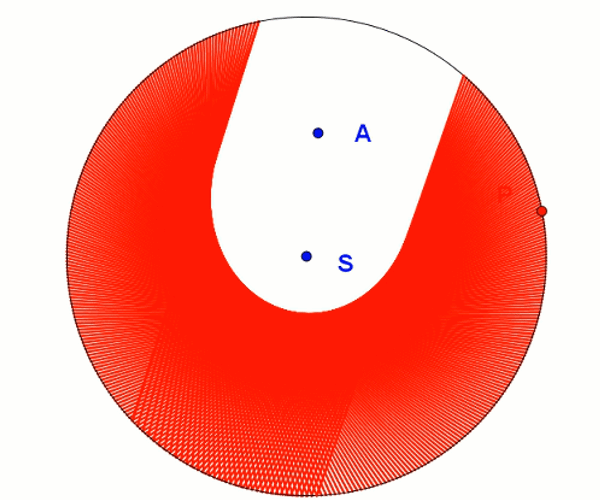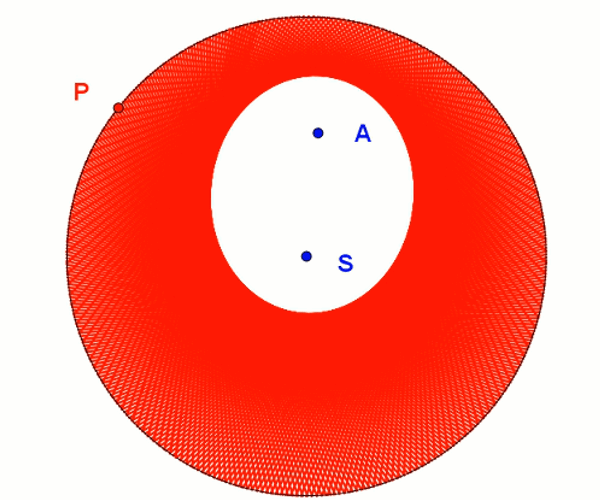
Elipsę możemy stworzyć przy pomocy kartki w kształcie koła. Poprzez odpowiednie zawijanie kartki uzyskamy kształt przypominający elipsę. Im gęściej będziemy zawijać kartkę, tym kształt będzie się bardziej upodabniał do elipsy. Możemy również wykonać animację działającą na tej samej zasadzie. Tworzymy okrąg i obieramy na nim dowolny punkt A. Na okręgu zaznaczamy punkt P wzdłuż którego będziemy "zaginać kartkę". Linią zagięcia będzie odcinek należący do symetralnej odcinka AP. Widzimy powstanie elipsy o ogniskach w punktach A oraz S.


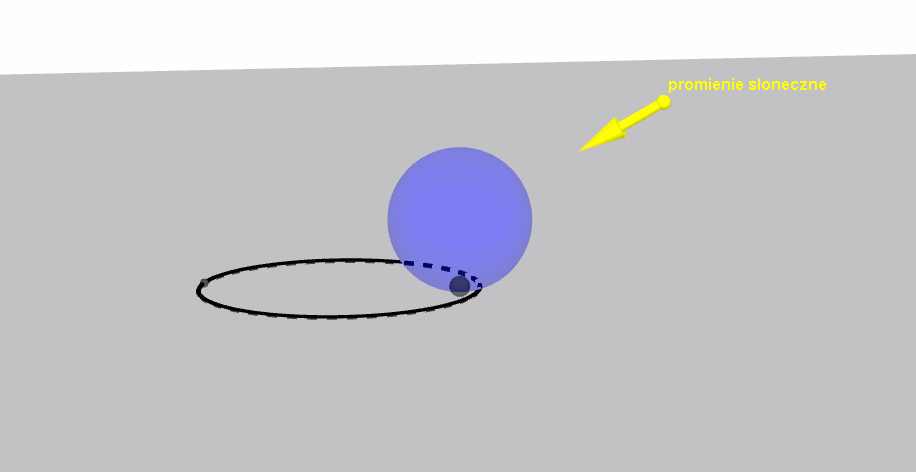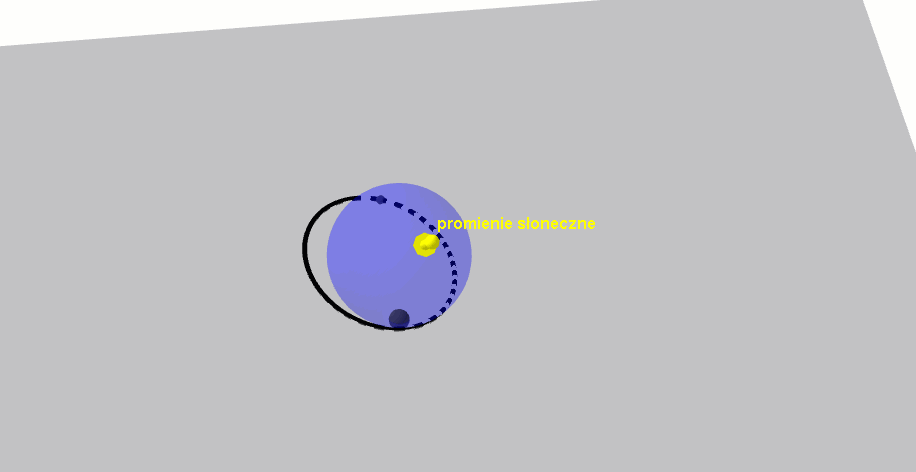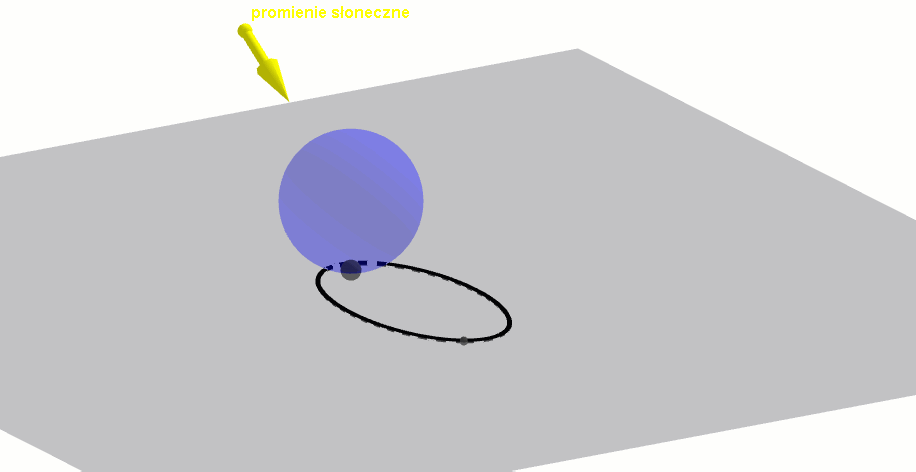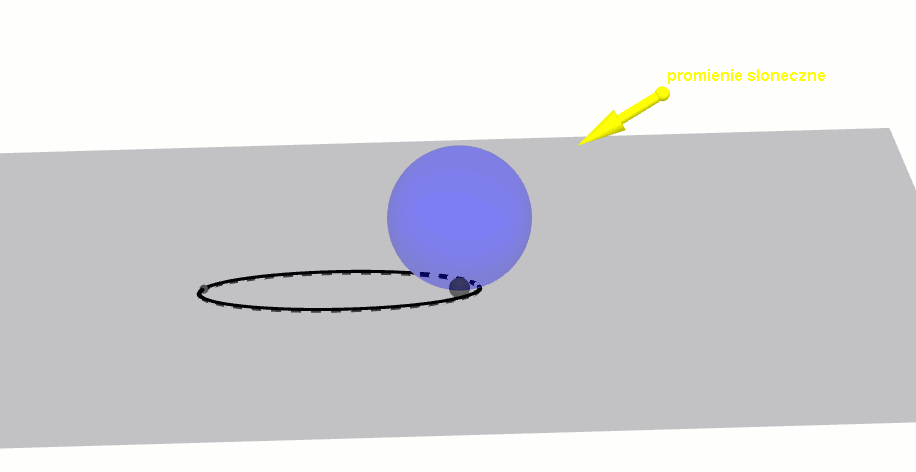
elipsa jako cień kuli
Już w starożytności grecki matematyk Archimedes zauważył, że cień kuli na jej podłożu stanowi zawsze elipsę, przy czym punkt styczności tej kuli jest jednym z ognisk elipsy.
złota elipsa
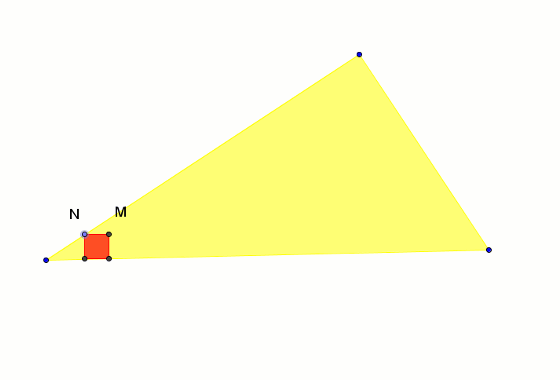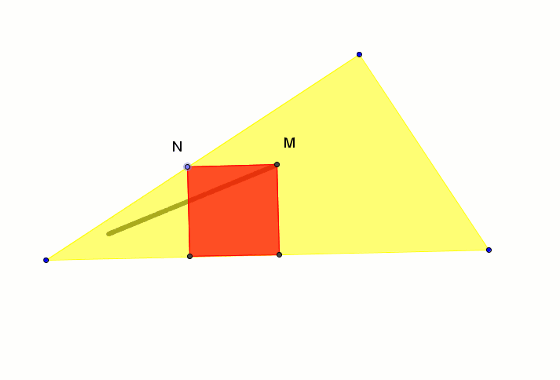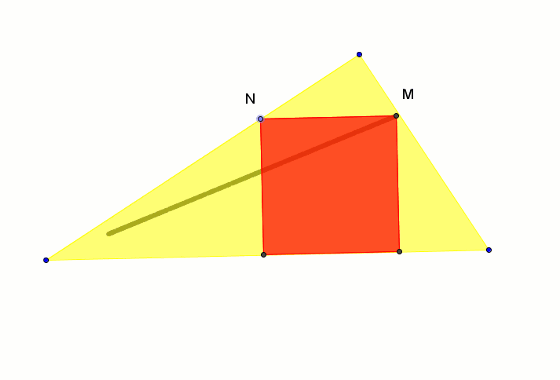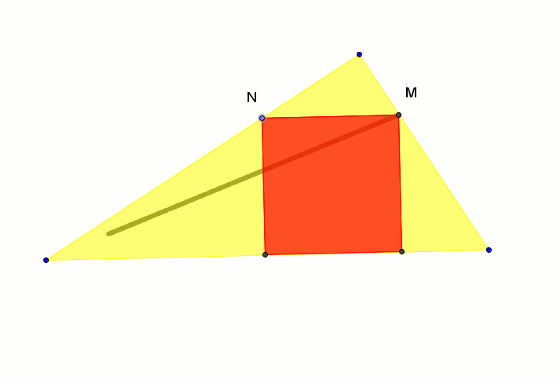
Znane jest zadanie polegające na umieszczeniu w trójkącie takiego kwadratu, by dwa jego wierzchołki leżały na podstawie, a dwa na jego bokach. Znany jest też sposób rozwiązania takiego zadania.
Kreślimy dowolny kwadrat, którego jeden z wierzchołków N porusza się po boku AC trójkąta ABC. Wówczas czwarty wierzchołek M tego kwadratu kreśli w trakcie poruszania punktem N półprostą wychodzącą z wierzchołka A trójkąta i przecinającą bok BC trójkąta w poszukiwanym punkcie. Wyznacza on rozwiązanie zdania.
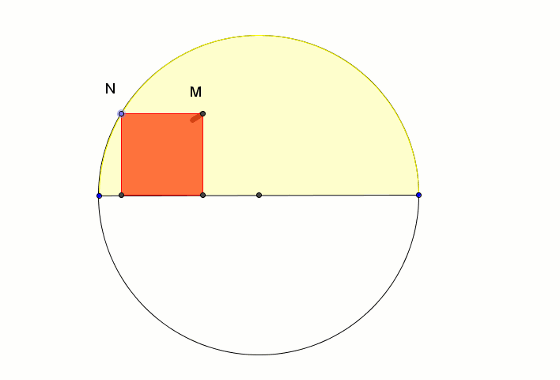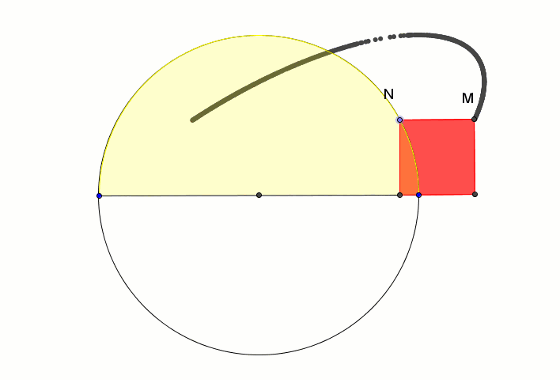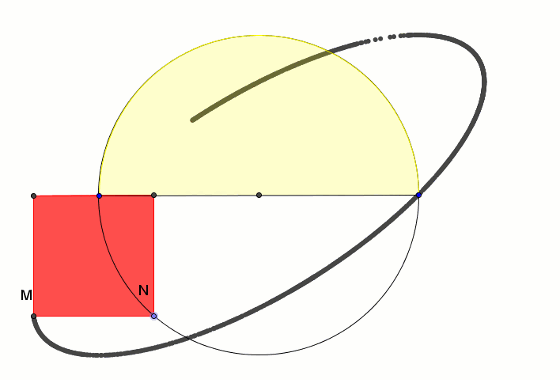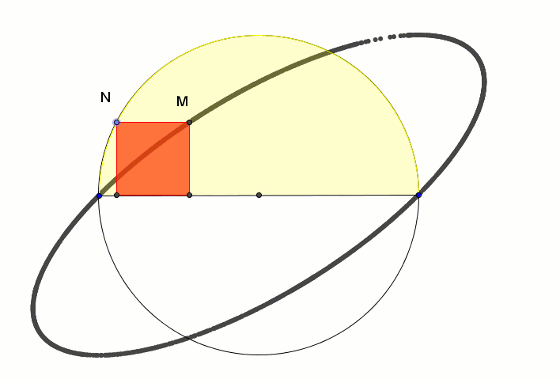
Wydawałoby się, że w taki sam sposób można skonstruować kwadrat umieszczony w półkolu tak, że jego dwa wierzchołki leżą na średnicy półkola, a dwa na półokręgu. Okazuje się tu wielkim zaskoczeniem, że tym razem wierzchołek M poszukiwanego kwadratu kreśli nie półprostą, lecz elipsę.
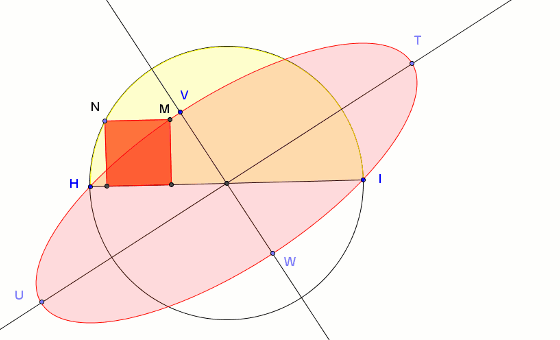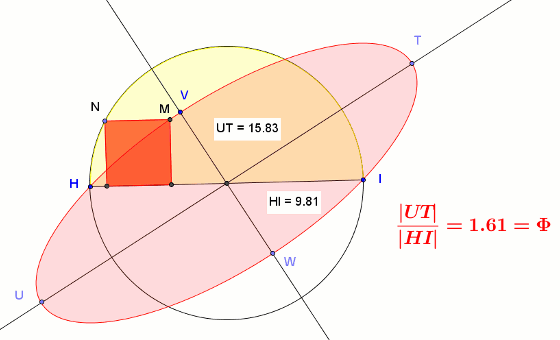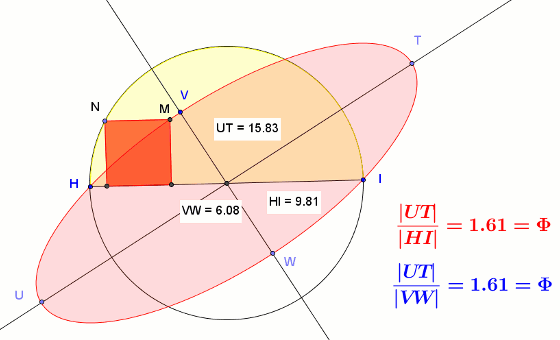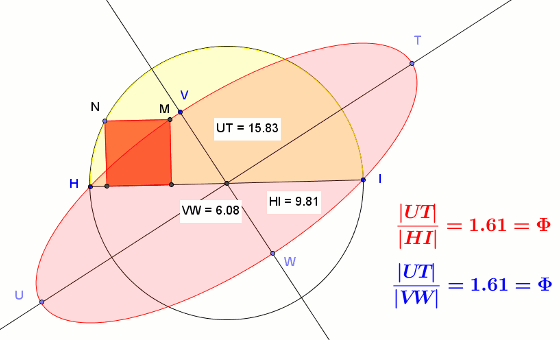
Okazuje się, że elipsa ta nie jest przypadkową elipsą. Stosunek długości jej wielkiej osi (|UT|) do średnicy półkola (|HI|) jest taki sam jak stosunek długości średnicy półkola (|HI|) do długości małej osi elipsy (|VW|) i jest równy dokładnie złotej liczbie φ = √5 + 12.
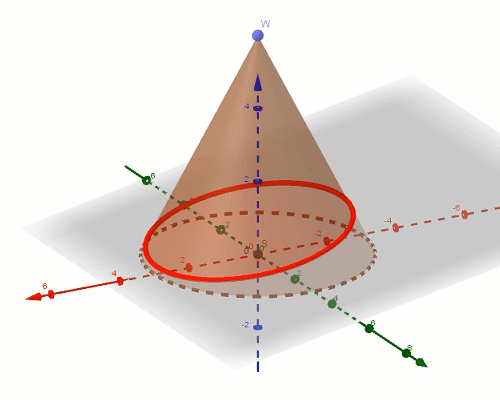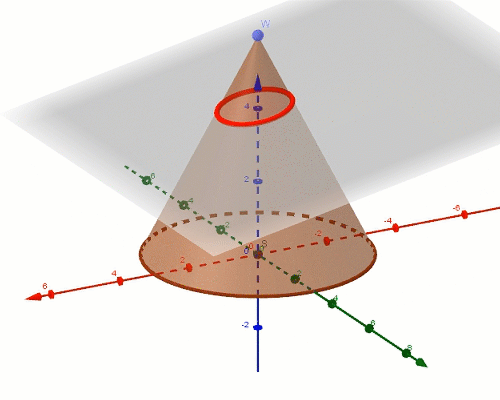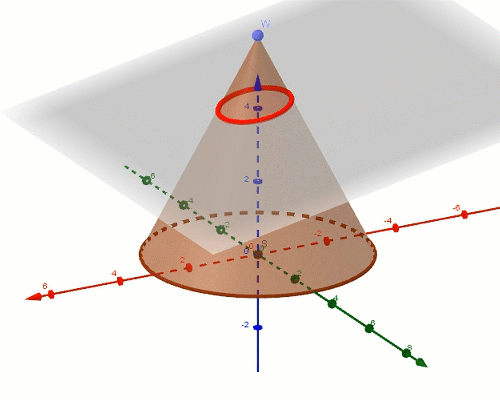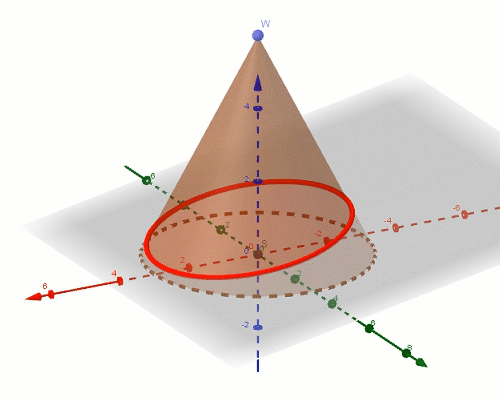
sfery dandelina
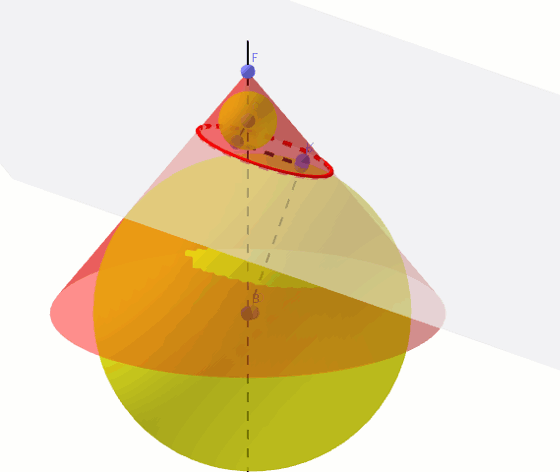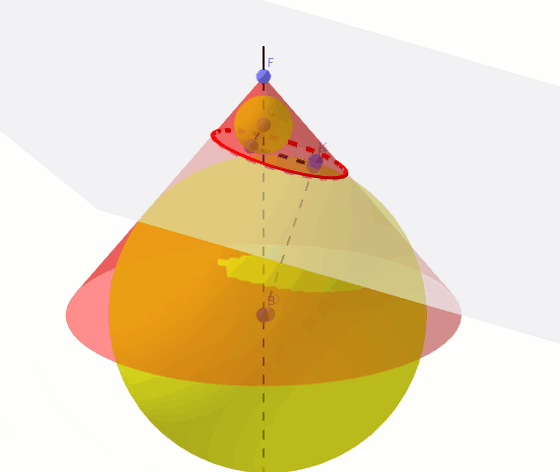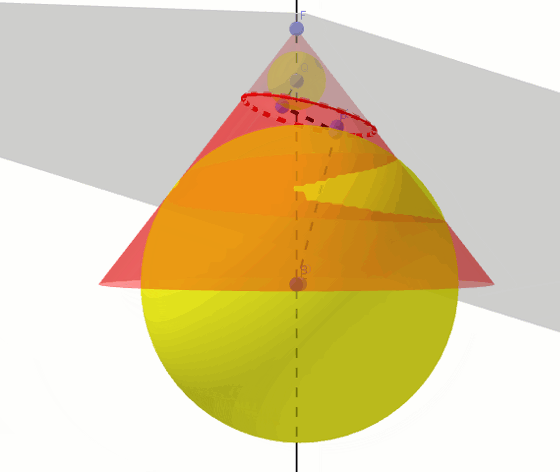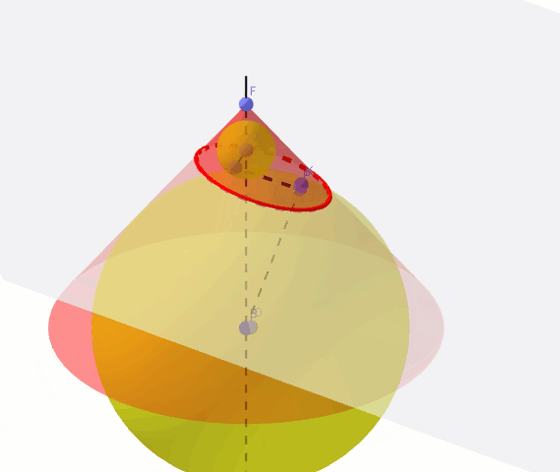
Sfery Dandelina to dwie sfery styczne do stożka i równocześnie do płaszczyzny, która w przecięciu ze stożkiem daje elipsę. Okazuje się, że punkty styczności sfer z płaszczyzną przekroju stanowią ogniska tej elipsy. Z powodu tych punktów styczności sfery te są też nazywane sferami ogniskowymi. Starożytni Grecy, m.in. Pappus z Aleksandrii znali definicję elipsy, ale nie potrafili udowodnić, że punkty styczności sfer są ogniskami tej elipsy. Dopiero Germinal Pierre Dandelin w XIXw. wykorzystując poniższą konstrukcję uzasadnił ten fakt. Sfery Dandelina pozwalają zauważyć zależności dzięki, którym da się dowieść prawdziwosci tego twierdzenia.
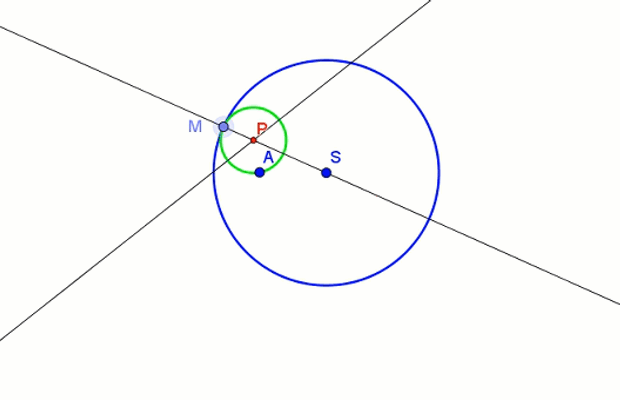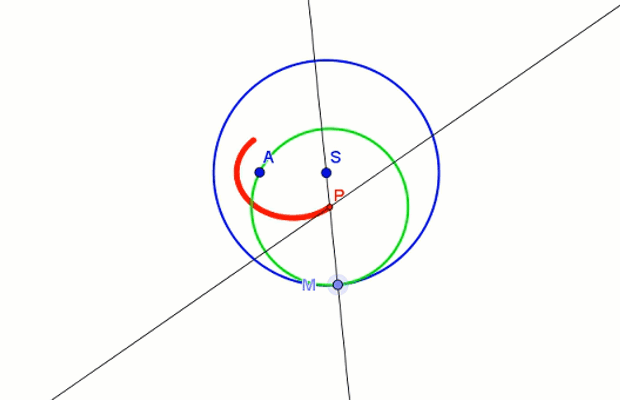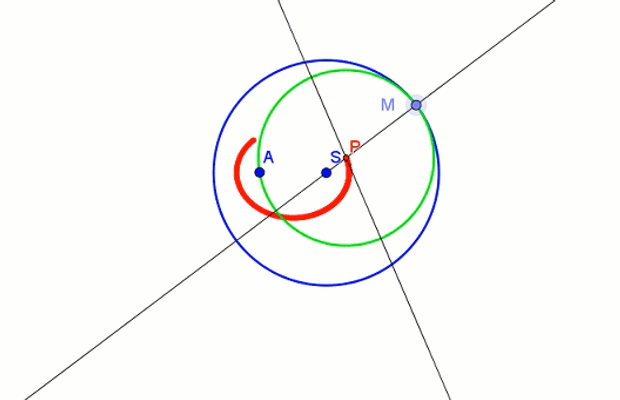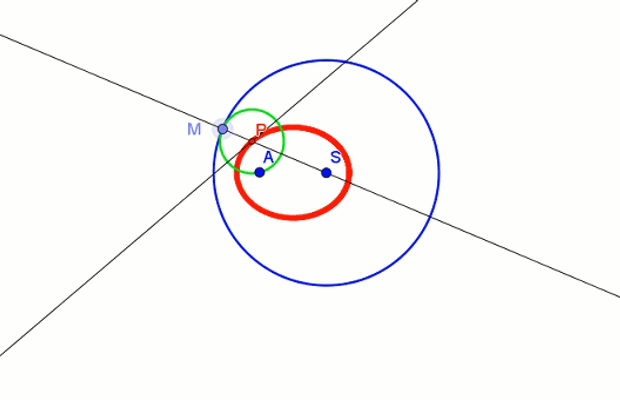
elipsa jako miejsce geometryczne środków okręgów
Elipsę można skonstruować jako miejsce geometryczne środków P okręgów stycznych do okręgu o środku S w punkcie M, przechodzących przez punkt wewnętrzny A koła tego okręgu.