spis treści
co nazywamy parabolą?
Parabola jest miejscem geometrycznym punktów równo oddalonych od ustalonej prostej zwanej kierownicą paraboli i ustalonego punktu zwanego ogniskiem paraboli.
tworzenie paraboli za pomocą sznurka
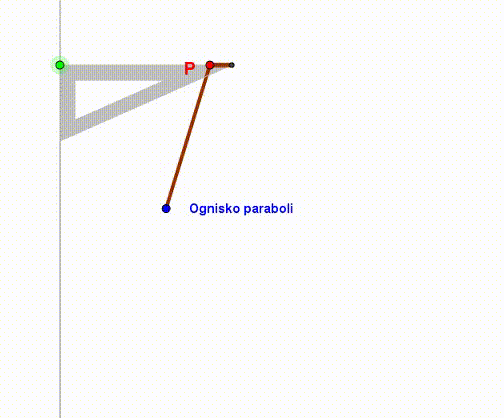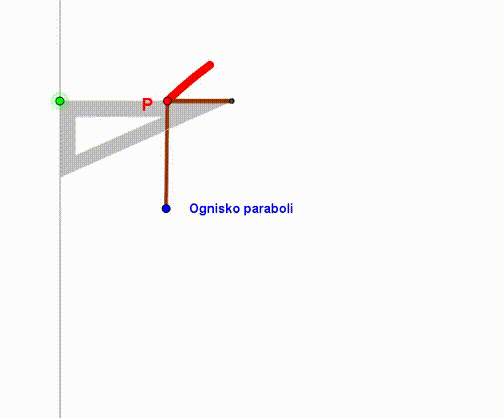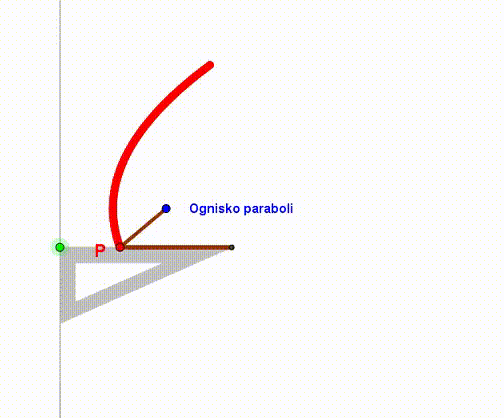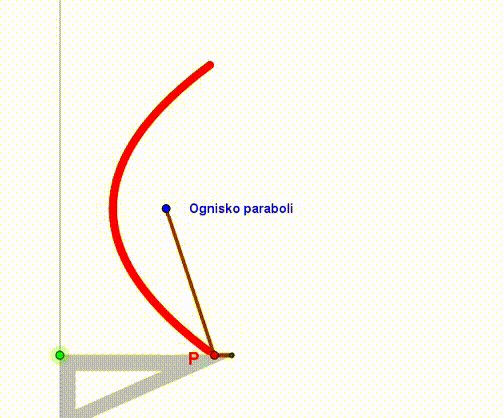
Parabolę możemy stworzyć przy pomocy linijki, ekierki i sznurka. Linijka będzie służyć za kierownicę. Jeden koniec sznurka mocujemy w wierzchołku ekierki, drugi zaś w ognisku paraboli (punkt F). Naciągamy sznurek przy krawędzi ekierki i przykładamy tam ołówek lub długopis. Ruszając ekierką wzdłuż kierownicy, ołówek zakreśli parabolę.
związek paraboli z ortocentrum trójkąta
Parabolę można uzyskać również rozważając ortocentrum trójkąta, w którym jeden z wierzchołków porusza się po prostej równoległej do przeciwległego boku tego trójkąta.
Wykonajmy w tym celu odpowiednią konstrukcję:
- niech odcinek AB będzie podstawą pewnego trójkąta
- poprowadźmy dowolną prostą k równoległą do odcinka AB,
- obierzmy na niej punkt C,
- zbudujmy trójkąt ABC,
- znajdźmy ortocentrum tego trójkąta i oznaczymy go jako pkt H.
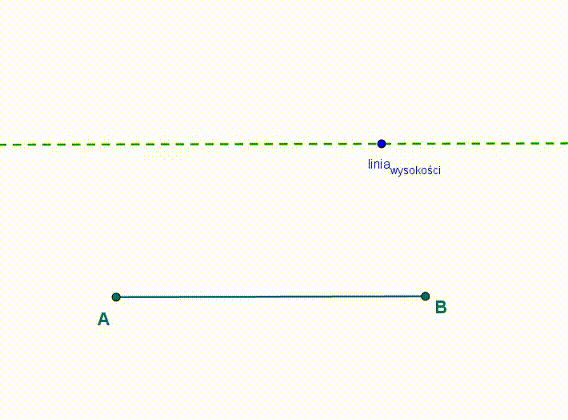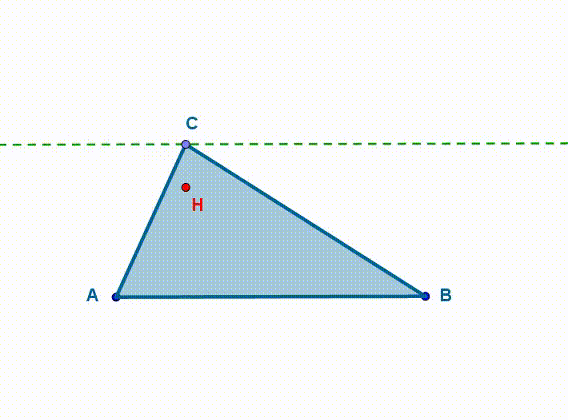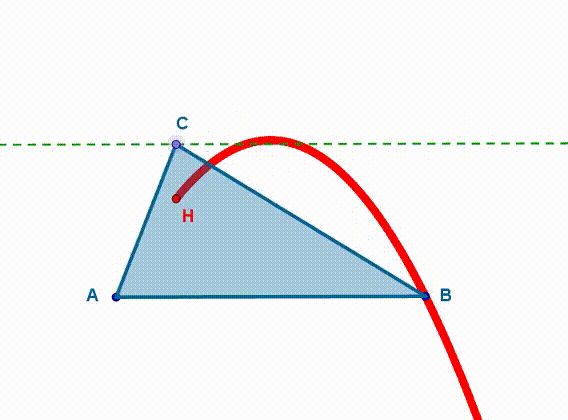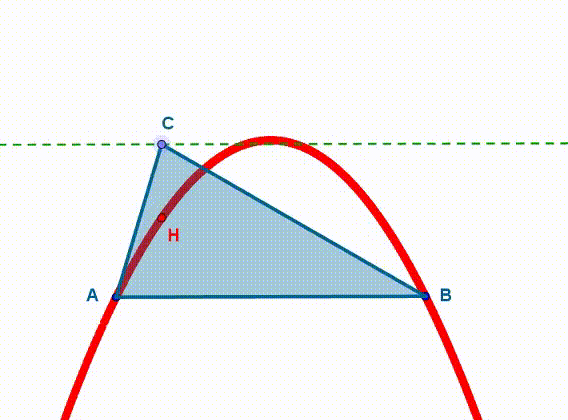
Okazuje się, że jeśli będziemy poruszać punktem C po prostej k, ortocentrum H trójkąta ABC zakreśla krzywą, która wydaje się parabolą.
Możemy tę konstrukcję umieścić w układzie współrzędnych i sprawdzić, czy da się dopasować wykres funkcji kwadratowej w postaci kanonicznej (aby można było łatwiej przesuwać wykresem wzdłuż osi) do paraboli zakreślanej przez ortocentrum.
Jeśli zmienimy długość podstawy AB, zauważymy, że parabola zakreślana przez punkt H jest taka sama, zmieniła tylko położenie. Zatem podstawa trójkąta nie ma wpływu na kształt paraboli.
Sprawdźmy teraz, jak zachowuje się parabola przy zmianie długości wysokości trójkąta poprowadzonej z wierzchołka C. Gdy prosta k oddala się od podstawy AB (czyli wysokość trójkąta wzrasta), tym ramiona paraboli stają się szersze (|a| maleje). W przeciwnym wypadku gałęzie paraboli stają się węższe.
Można udowodnić, że równanie paraboli, jaką zakreśla ortocentrum trójkąta o podstawie AB i wysokości h wyraża się wzorem y = -1hx2 + ABhx (dowód tego faktu znajduje się w pozycji [3]).
okrąg carlyle'a
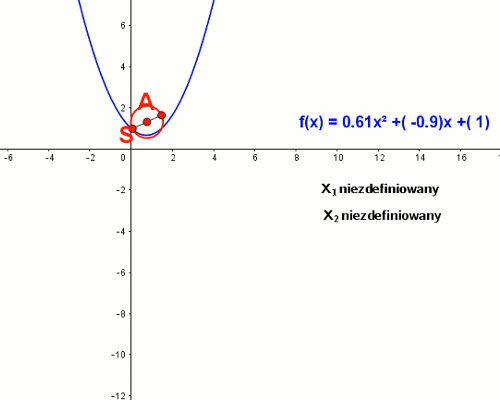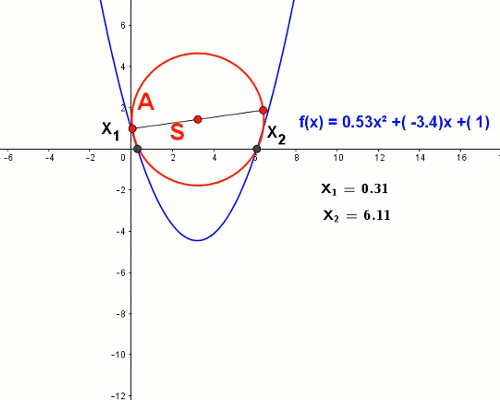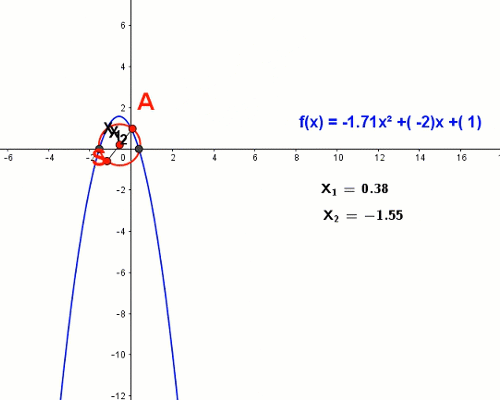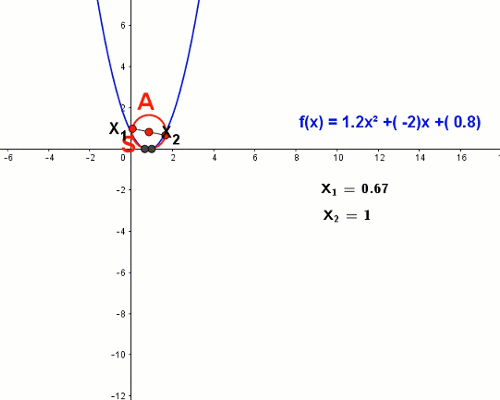
Parabola jest wykresem funkcji wielomianowej stopnia drugiego, zwanej trójmianem kwadratowym. Miejsca zerowe funkcji kwadratowej oblicza się za pomocą wyróżnika trójmianu kwadratowego. Okazuje się, że miejsca zerowe trójmianu kwadratowego możemy odczytać geometrycznie kreśląc cyrklem odpowiedni okrąg.
Odkrycie to zawdzięczamy szkockiemu historykowi Thomasowi Carlyle’owi. Średnicą tego okręgu jest odcinek AB o końcach A = (0,1) oraz B = (-ba,ca)

(1795 - 1881)
Zmieniając wartości współczynników funkcji kwadratowej widzimy jak za każdym razem okrąg Carlyle'a przecina oś odciętych w miejscach zerowych wykresu.
Jak widać niektóre problemy algebraiczne można rozwiązywać geometrycznie.
wyznaczanie pola między parabolą i jej cięciwą
Aby wyznaczyć pole między parabolą, a jej cięciwą zazwyczaj posługujemy się całkami. Wspomniany wcześniej Archimedes interesował się wyznaczaniem pól nietypowych figur. Jednym z jego zainteresowań była parabola i pole pomiędzy nią i cięciwą AB. Archimedes obrał środek cięciwy AB i poprowadził przez niego prostą równoległą do osi paraboli. Punkt przecięcia paraboli z tą prostą oznaczmy jako punkt C.
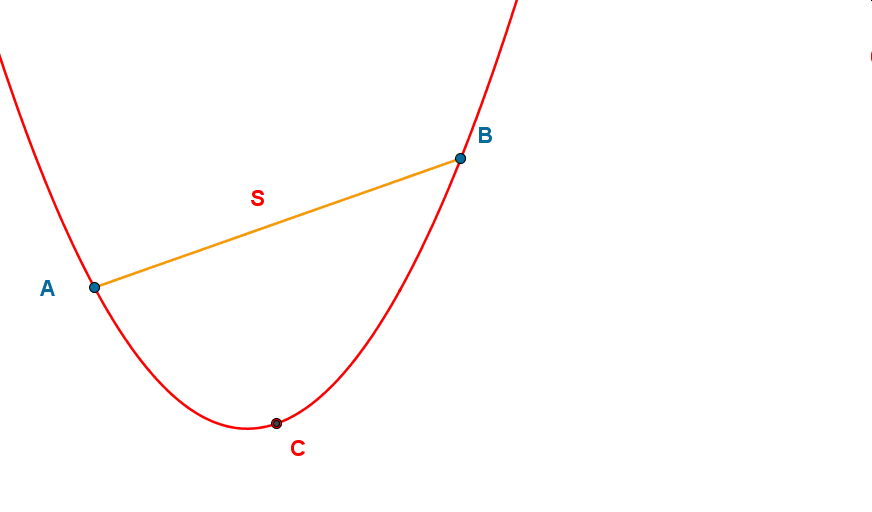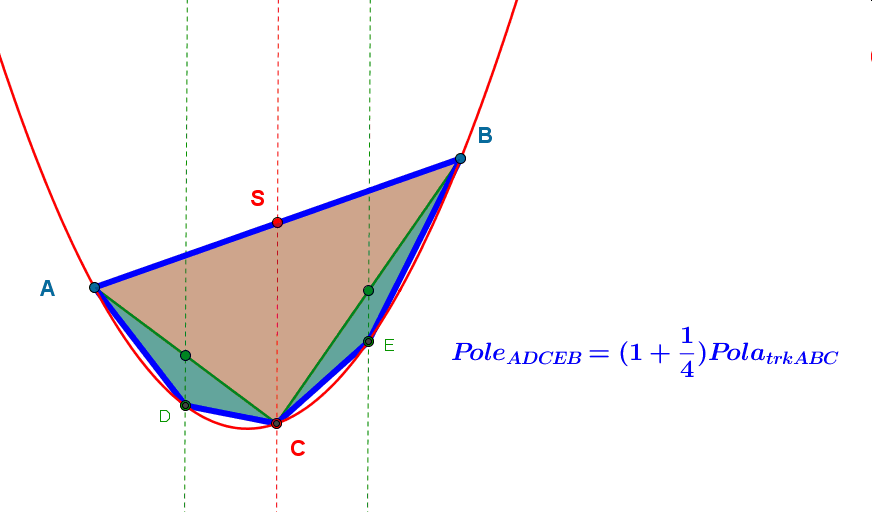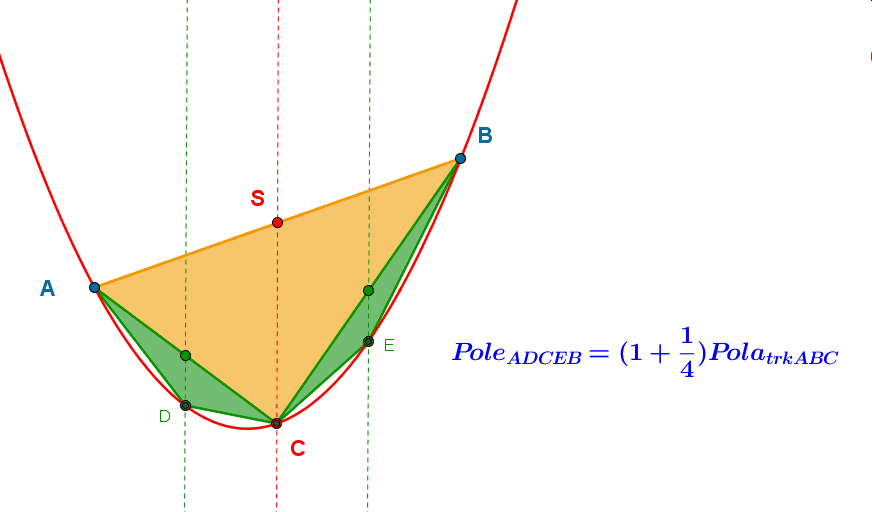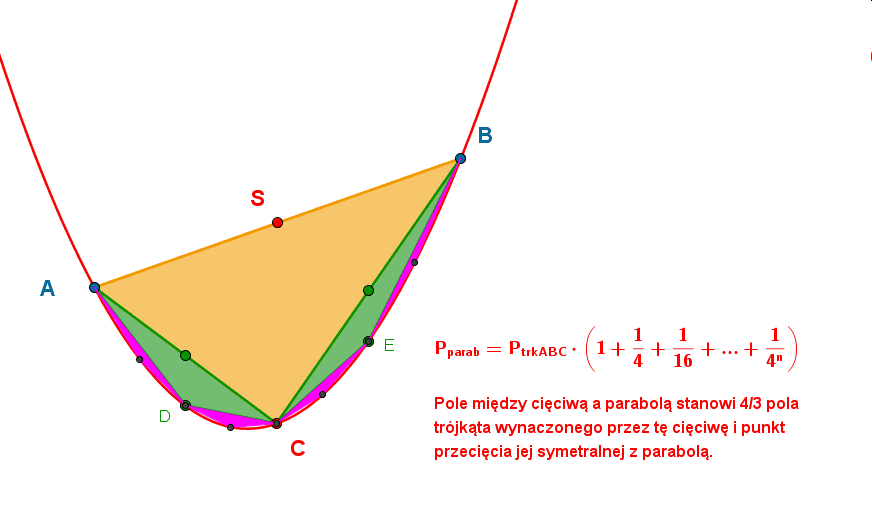
Podobnie uczyńmy z cięciwami AC i BC i wyznaczmy dwa kolejne trójkąty. Okazuje się, że pola tych trójkątów są równe i stanowią 18 PABC.
Pole wielokąta ADCEB jest sumą pola trójkąta ABC i 14 pola tego trójkąta.
Powtarzajmy te czynność dalej i twórzmy kolejne trójkąty na bazie cięciw, aż wypełnimy nimi cały obszar pomiędzy parabolą, a cięciwą AB.
Otrzymamy wówczas: Poleparaboli = PoleABC (1 + 14 + 116 + ... + 14n+ ...). Suma ułamków w nawiasie to suma nieskończonego szeregu geometrycznego. Jego wartość wynosi 43. Dochodzimy zatem do wniosku, iż pole między cięciwą, a parabolą stanowi 43 pola trójkąta wyznaczonego przez tę cięciwę i punkt przecięcia jej symetralnej z parabolą. Archimedesa uznaje się za prekursora rachunku całkowego. Opisana tutaj metoda przybliża sposób jego "całkowania".
jak zniszczyć wrogą flotę lustrem parabolicznym
Według zapisków bizantyjskiego kronikarza Joannesa Zonarasa oraz ustnie przekazywanych podań, grecki naukowiec i wynalazca Archimedes skonstruował specjalne lustra, którymi jak głosi opowieść, spalił statki wroga podczas oblężenia Syrakuz przez Rzymian. W lustrze takim wszystkie promienie równolegle do osi symetrii są po odbiciu od lustra skupiane w jego ognisku. Prawdopodobnie tę własność Archimedes wykorzystał do skierowania promieni słonecznych i skupienia ich na okrętach floty rzymskiej.

Bitwa pod Syrakuzami
zastosowania zwierciadeł parabolicznych
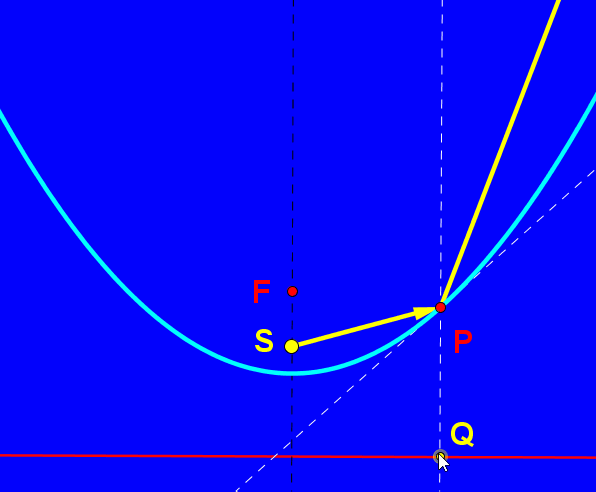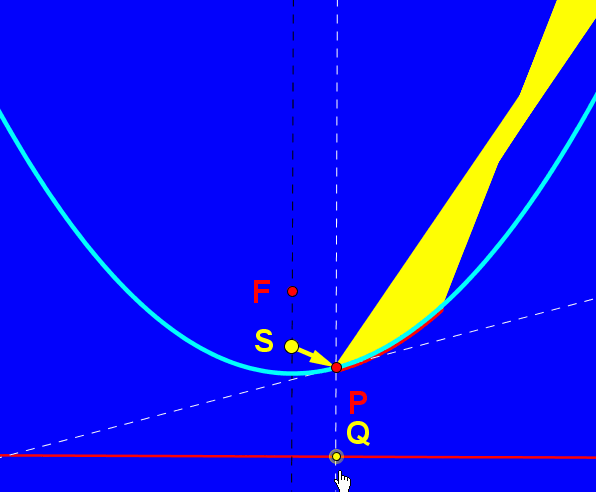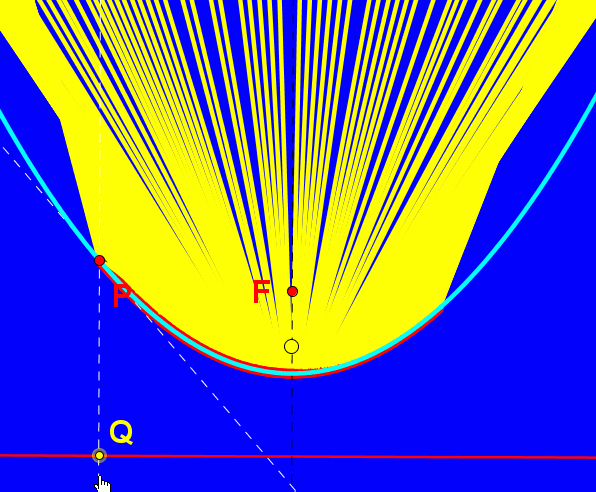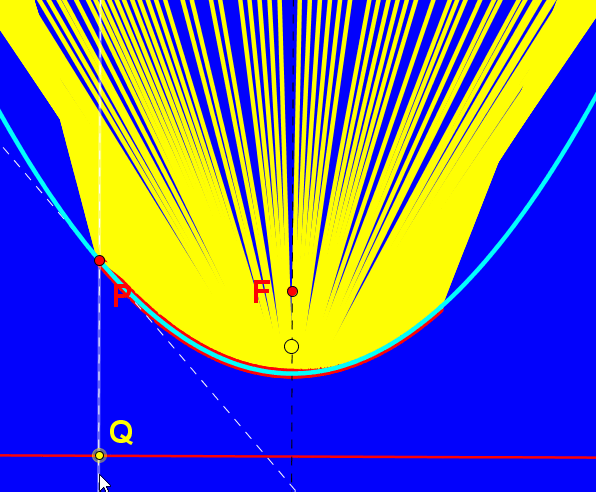
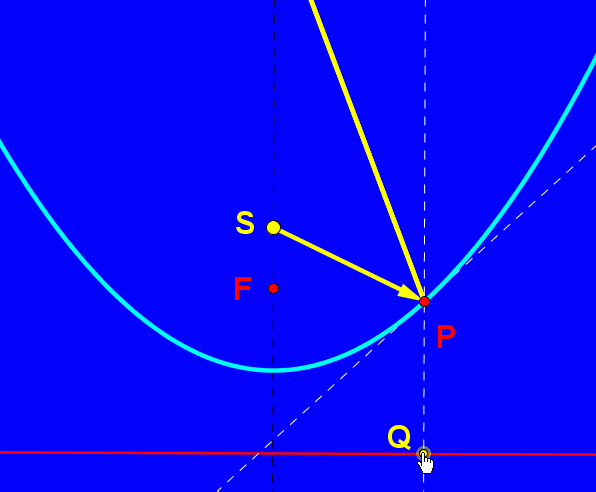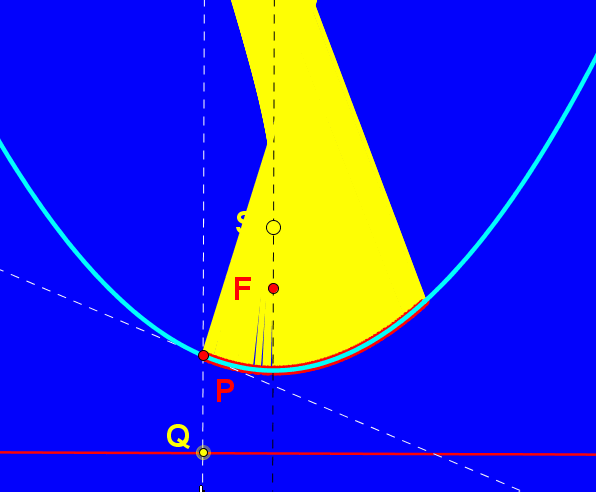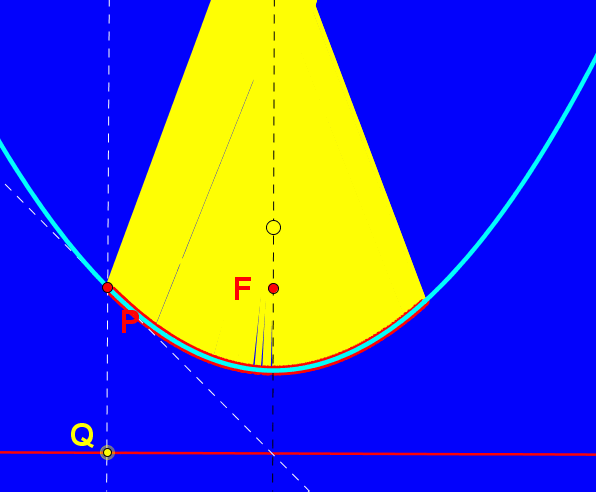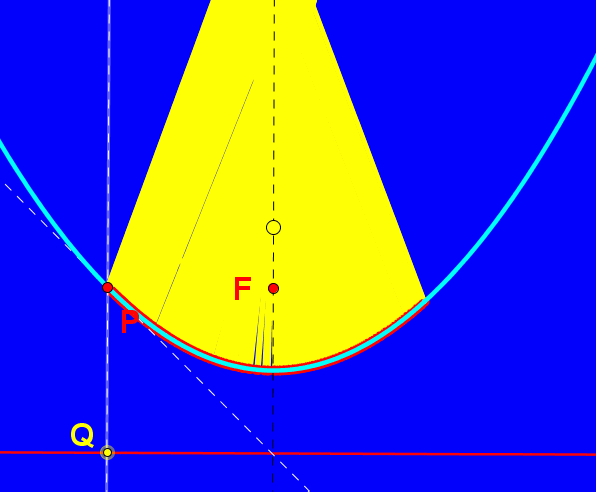
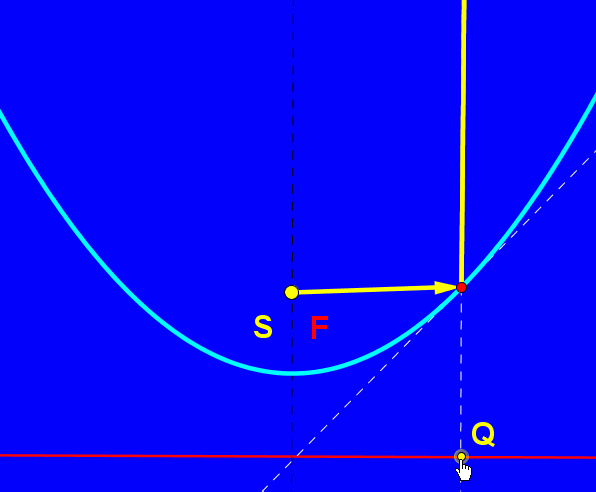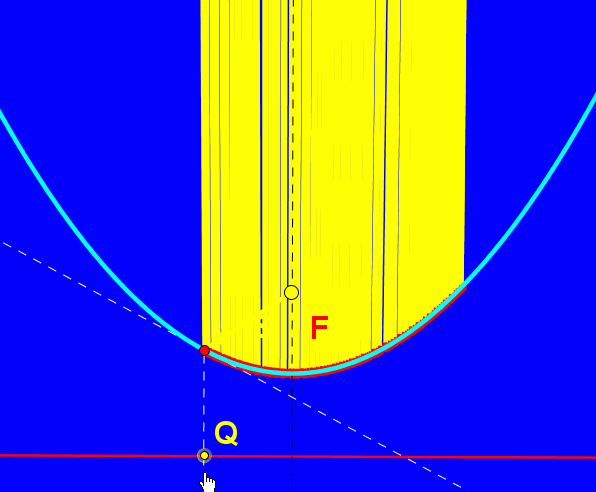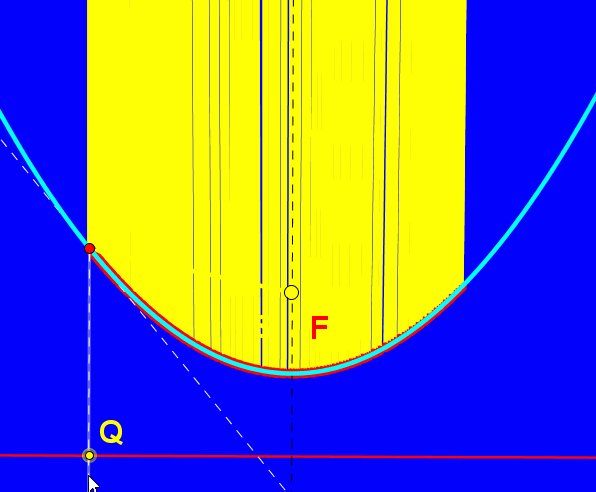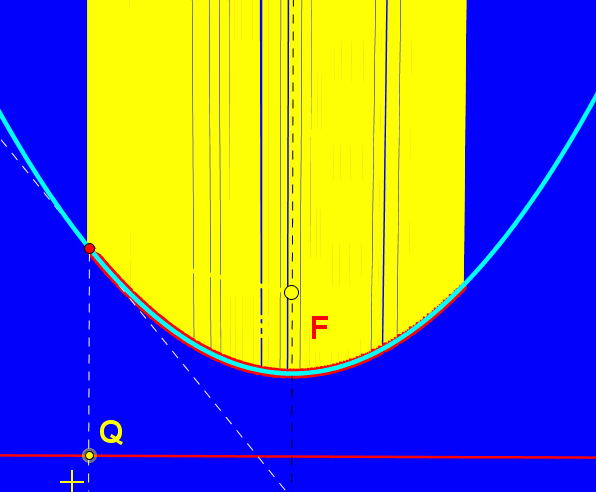
W współczesnym świecie zwierciadła paraboliczne odgrywają istotną rolę w konstruowaniu m.in. reflektorów samochodowych, teatralnych i anten satelitarnych. Umieśćmy źródło światła na osi symetrii lustra, oznaczmy je jako punkt S. Promień odbija się od zwierciadła i daje nam promień odbity zgodnie z zasadą równości kąta padania i odbicia. Jeśli źródło światła znajduje się między wierzchołkiem paraboli i jej ogniskiem mamy do czynienia ze światłami mijania, umieszczając źródło światła "przed" ogniskiem tworzymy snop świateł drogowych. W reflektorach teatralnych źródło światła umieszczone jest w ognisku lustra.
parabola w architekturze
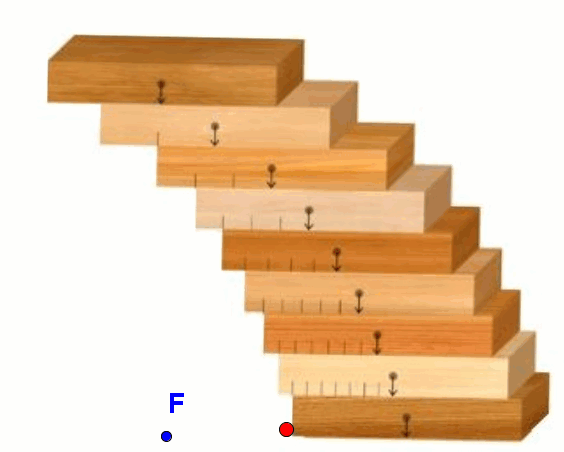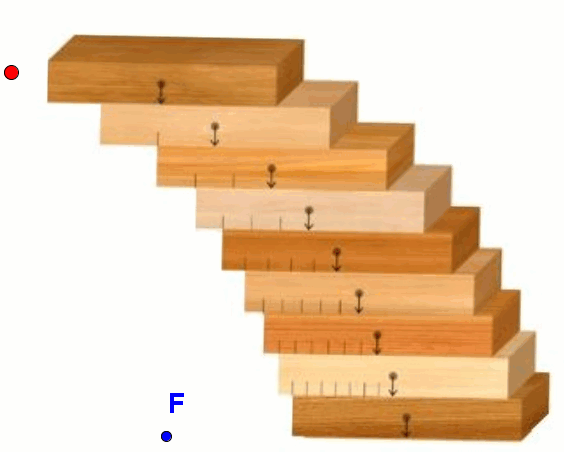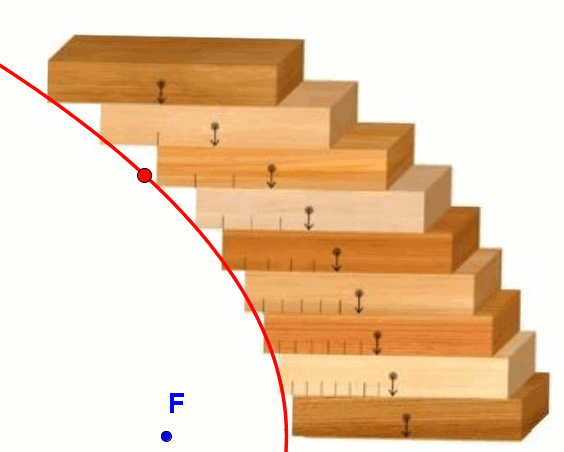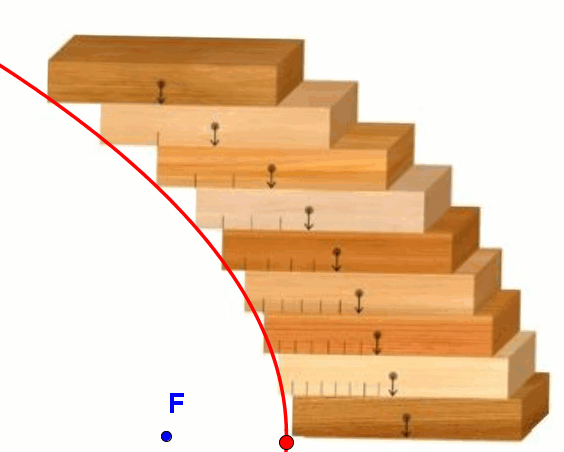
Jeśli ułożymy stos klocków tak, aby środek ciężkości każdego z nich był tak zachowany, że klocki te nie przewrócą się, wówczas krawędzie klocków ułożą się w kształcie fragmentu paraboli. Takie ustawienie klocków (lub cegieł itp.) służy od wieków przy budowie łuków parabolicznych, wiaduktów i mostów.