Transformacje dwuwymiarowe dotyczą wielokątów na płaszczyźnie dwuwymiarowej. Przy ich konstrukcji wykorzystujemy przekształcenia izometryczne: przesunięcia, obroty, symetrie osiowe i środkowe.
Transformacje Dwuwymiarowe
Problem Haberdasher’a
Jak podzielić trójkąt równoboczny na cztery części, z których będziemy w stanie ułożyć kwadrat. Problem postawiony w 1902 roku przez Henrego Dudeney’a.
Zacznijmy od skonstruowania trójkąta równobocznego i podzieleniu go na odpowiednie części. Znajdujemy środki ramion trójkąta (punkt D oaz punkt E) i prowadzimy przez te punkty proste prostopadłe do podstawy AC naszego trójkąta. Zaznaczamy punkty przecięcia tych prostych z podstawą AC (punkt F oraz punkt G). Konstruujemy odcinek EF, a następnie proste prostopadłe do tego odcinka przechodzące prze punkty D i E. Pozwoli to na znalezienie punktu H oraz punktu I. Teraz tworzymy odpowiednie wielokąty, których wierzchołkami są punkty, które wcześniej wyznaczyliśmy.
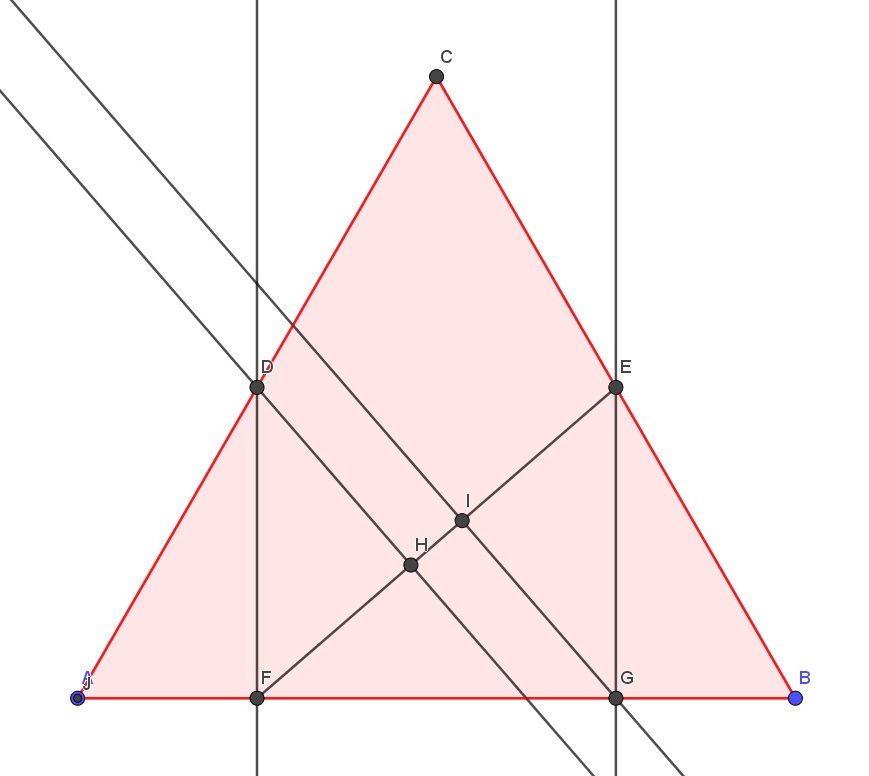
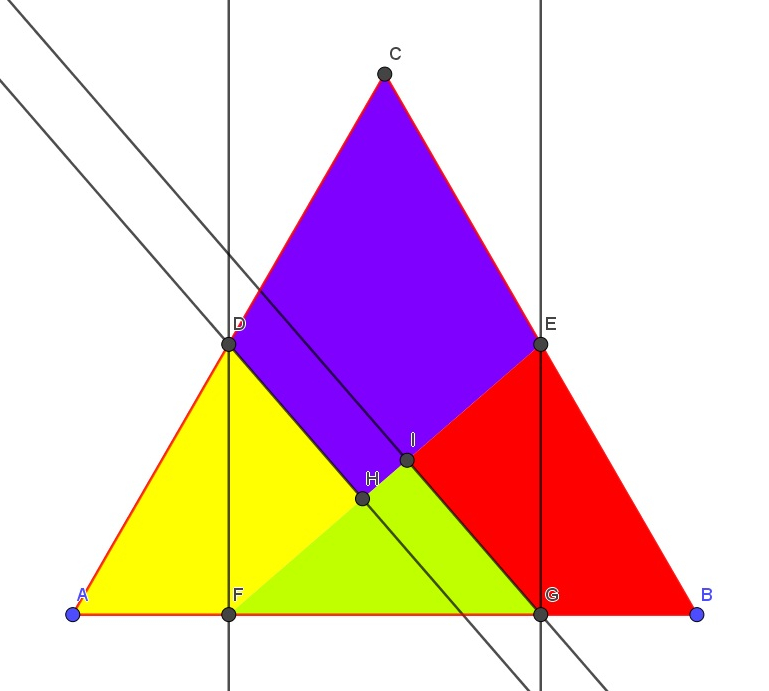
Po stworzeniu odpowiednich wielokątów wewnątrz trójkąta możemy obrócić je wokół odpowiednich punktów aby otrzymać kwadrat. Prezentuje to Aplet 4.
Uogólniając problem Haberdasher’a na inne wielokąty możemy szukać podziału n-kątnego wielokąta na mniejsze wielokąty, który odpowiednio pocięty będzie mógł przekształcić się w k-kątny wielokąt. Na przykład poszukujemy podziału kwadratu na pięć części aby przekształcić go w pięciokąt. Oczywiście taki rozkład już został odkryty. Poniżej prezentujemy kilka przykładów.
Transformacja ośmiokąta foremnego w kwadrat
Zacznijmy od skonstruowania ośmiokąta foremnego. Następnie na dwóch parach przeciwległych boków szukamy środków tych odcinków (punkty: I, J, K, L). Następnie w punkcie L konstruujemy okrąg o promieniu o długości boku ośmiokąta. Przecięcie okręgu z bokiem FE wyznacza punkt N. Warto nadmienić, iż punkt N nie jest środkiem boku FE. Następnie wyznaczamy punkty O, P, Q, R. Aby to zrobić tworzymy prostą NK i następnie prostą równoległą do tej prostej przechodzącej przez punkt L oraz dwie proste prostopadłe do prostej NK przechodzące przez punkt I oraz punkt J. Przecięcia tych prostych wyznaczają punkty, które będą wierzchołkami kwadratu.
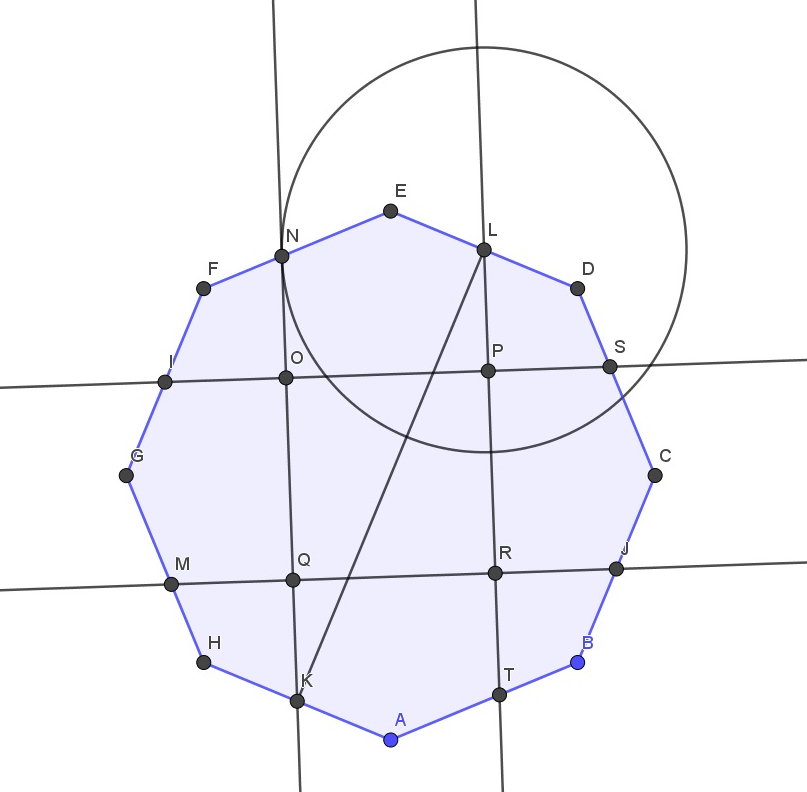
Następnie dzielimy ośmiokąt na wspomniany kwadrat i 4 pięciokąty. Teraz wystarczy obrócić odpowiednio pięciokąty aby otrzymać kwadrat.
Transformacja dwunastokąta foremnego w kwadrat
Dwunastokąt foremny w sześć przystających kwadratów
Disekcja Grega Fredericksona
W dwunastokącie foremnym kreślimy przekątne. Mogą one mieć trzy różne długości. Dla nas istotne będą przekątne między którymi zawierają się cztery krawędzie dwunastokąta. Następnie zaznaczamy punkty w odpowiednich przecięciach tych przekątnych. Znajdujemy także środek dwunastokąta, który jest środkiem jego symetrii. Następnie pomiędzy wierzchołkami i wyznaczonymi punktami tworzymy trójkąty i pięciokąty.
Widzimy, iż obszar pomiędzy trójkątami i pięciokątami to również dwunastokąt foremny. Czy jesteśmy w stanie ustalić jaką część pola dużego dwunastokąta stanowi jego pole? Odpowiedź uzyskamy animując Aplet 8.
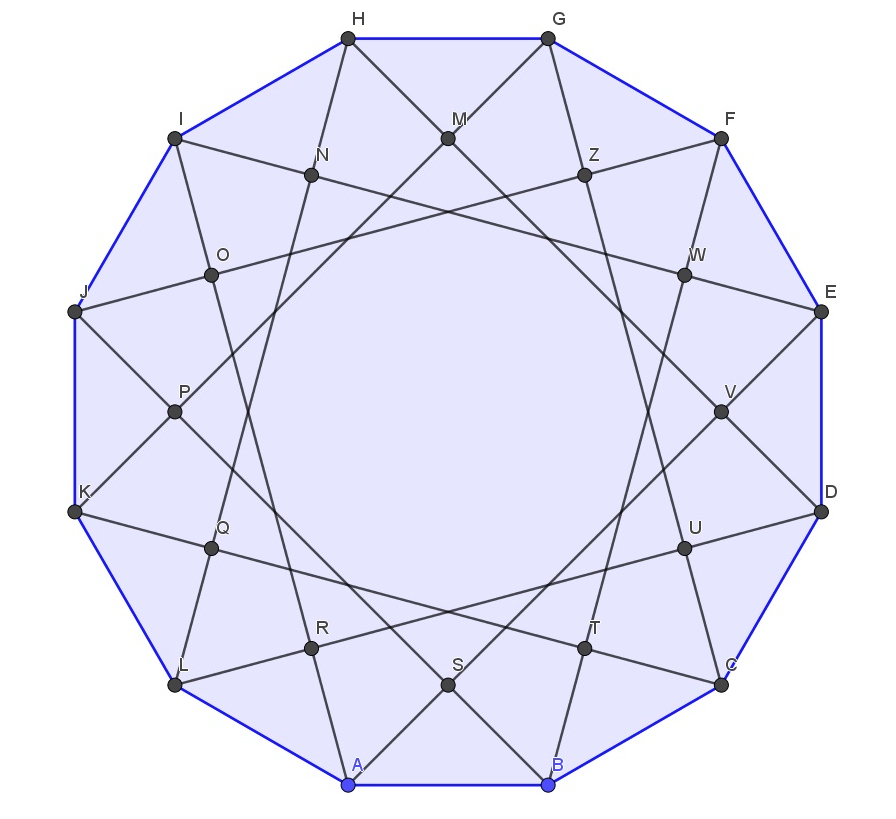
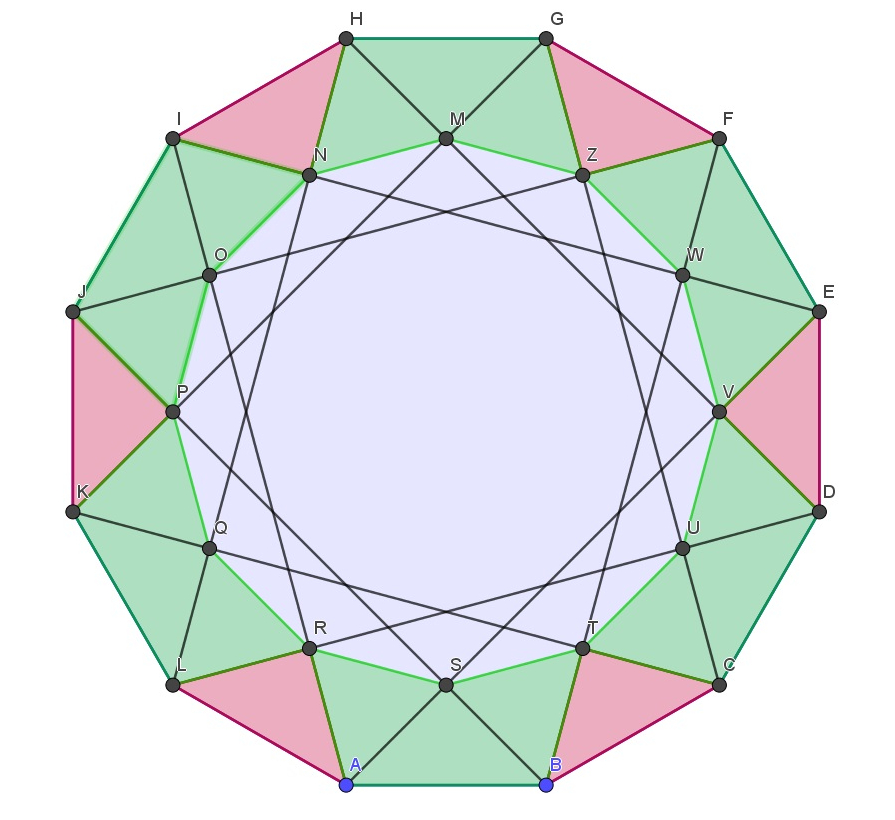
Pole nowopowstałego dwunastokąta jest równe połowie powierzchni dwunastokąta bazowego.
Pole kwadratu utworzonego w kwadracie
W zbiorach zadań pojawia się zadanie o następującej treści: W kwadracie o polu 25 jednostek kwadratowych wpisano odcinki łączące każdy wierzchołek z kwadratu z środkiem przeciwległego boku. Uzyskano w ten sposób nowy kwadrat wewnątrz tego kwadratu. Jakie jest pole tak utworzonego kwadratu.
Oto dynamiczne rozwiązanie tego problemu geometrycznego bez użycia rachunków. Kwadrat bazowy składa się z kwadratu, z 4 trapezów i 4 trójkątów prostokątnych. Jeżeli trójkąty te obrócimy o 180 stopni wokół odpowiedniego ich wierzchołka to otrzymana figura będzie krzyżem o tym samym polu co kwadrat. Widać, że pole środkowego kwadratu jest równe ⅕ pola kwadratu bazowego czyli wynosi 5 jednostek.