Wstęp

Czym są transformacje?

Transformacją wielokąta (wielościanu) w inny wielokąt (wielościan) nazywamy takie przekształcanie części jednego z nich (na przykład przez rozcięcie), dzięki którym uzyskujemy drugi obiekt o innych własnościach.

Od tangramu do twierdzenia Bolyai-Gerwiena

Matematyków od czasów starożytnych interesował problem rozcięcia wielokąta na inny wielokąt o tym samym polu. Pierwszymi problemami polegającymi na takim rozcinaniu były tangramy.

Tangram (układanka z siedmiu elementów zwanych tanami) był znany już w Starożytnych Chinach. Najbardziej popularnym jest układanka składająca się z pięciu trójkątów, kwadratu i równoległoboku, których sumę stanowi pewien kwadrat. Czy da się skonstruować z tych kawałków dwa przystające kwadraty ? Można zauważyć, że istnieją takie dwa kwadraty, których długość boku jest równa połowie długości przekątnej wyjściowego kwadratu.

Doświadczenie to wskazuje na możliwość rozcięcia dwóch przystających kwadratów na mniejsze części, z których da się stworzyć jeden większy kwadrat. Pójdźmy o krok dalej i sprawdźmy czy da się stworzyć jeden kwadrat z dwóch mniejszych kwadratów o różnych długościach boków.

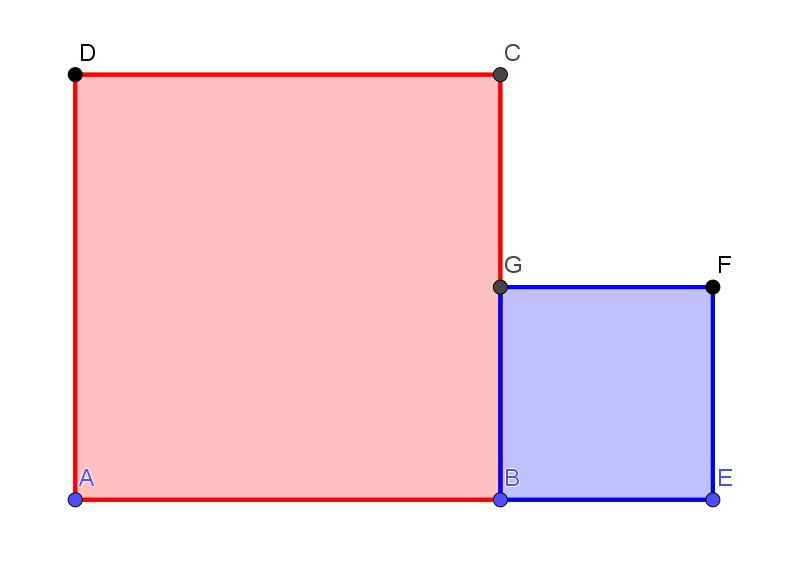
Dane są dwa kwadraty o różnych długościach boków. Chcemy teraz znaleźć bok większego kwadratu, którego pole jest sumą dwóch kwadratów o bokach a = AB i b = BE. Kreślimy je tak aby punkt B był wspólnym wierzchołkiem obu kwadratów. Od wierzchołka A odkładamy na boku AB odcinek b. Otrzymamy punkt H. Trójkąt HEF jest trójkątem prostokątnym o bokach HE = a i EF = b. Zatem odcinek HF = x jest bokiem poszukiwanego kwadratu, gdyż z twierdzenia pitagorasa x² = a² + b². Z oczywistych powodów trzeci wierzchołek poszukiwanego kwadratu to punkt D.

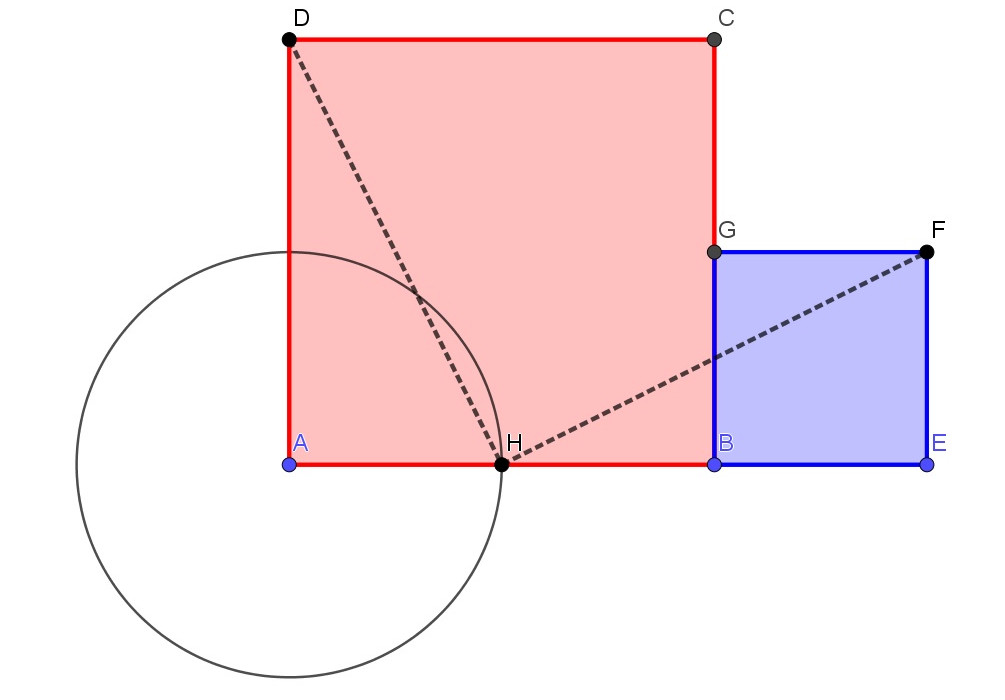
Można dostrzec, że nasze kwadraty zostały podzielone na dwa trójkąty oraz pięciokąt. Jak otrzymać z nich poszukiwany kwadrat? Poruszajmy suwakiem na Aplecie 1.

Pójdźmy o krok dalej i postawmy pytanie:

Czy jeżeli dwa dowolne wielokąty mają takie same pola to z jednego podzielonego na skończoną liczbę mniejszych wielokątów da się złożyć drugi?

Każdy wielokąt o n wierzchołkach da się podzielić na n-2 trójkąty. Operację tę nazywamy triangulacją wielokąta. Natomiast każdy trójkąt możemy rozciąć tak, aby otrzymać prostokąt.

Oto opis tej operacji.

Konstruujemy dowolny trójkąt. Wyznaczamy jego wysokość, szukamy środka tej wysokości (punkt E) i konstruujemy prostą równoległa do podstawy, na którą opuszczona jest wysokość, przechodzącą przez punkt E. Zaznaczamy punkty wspólne prostej i ramion trójkąta (punkt F oraz punkt E). Warto zauważyć, że punkty te są środkami ramion trójkąta.

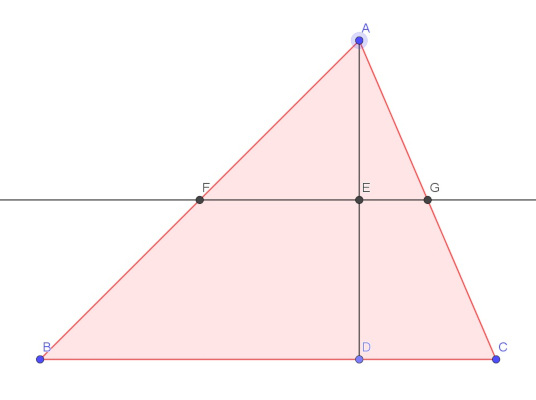
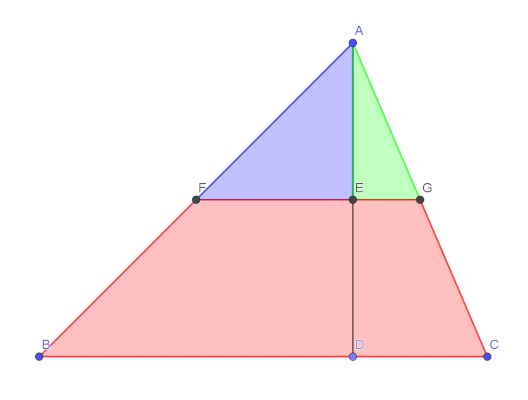
Wyznaczają one dwa trójkąty: FEA oraz EGA, a poniżej prostej FG powstaje trapez BCGF. Poruszając suwakiem uzyskamy obrót tych trójkątów tworzących wraz z trapezem poszukiwany prostokąt.

Potrafimy już każdy z trójkątów triangulacji wielokąta rozciąć na prostokąt o takim samym polu co trójkąt. Spróbujmy teraz każdy z tych prostokątów rozciąć tak, aby uzyskać kwadrat o tym samym polu co prostokąt.

Jeśli prostokąt ma wymiary a × b to z tego warunku uzyskujemy równanie ab=x², gdzie x jest długością boku kwadratu. Kreślimy prostokąt ABCD, gdzie |AB|=a , |BC|=b. Kreśląc okrąg o środku A i promieniu b, otrzymujemy w przecięciu z prostą AB punkt D'. Kreślimy okrąg o środku E traktując odcinek b jako jego promień. W punkcie A wystawiamy prostopadłą do odcinka AB otrzymując w przecięciu z okręgiem punkt M . Długość AM jest równa √ab (twierdzenie o średniej geometrycznej). Odcinek AM jest zatem bokiem poszukiwanego kwadratu. Aby przekształcić nasz prostokąt wyznaczamy: trójkąty KBN i BCF oraz pięciokąt AKNFD.

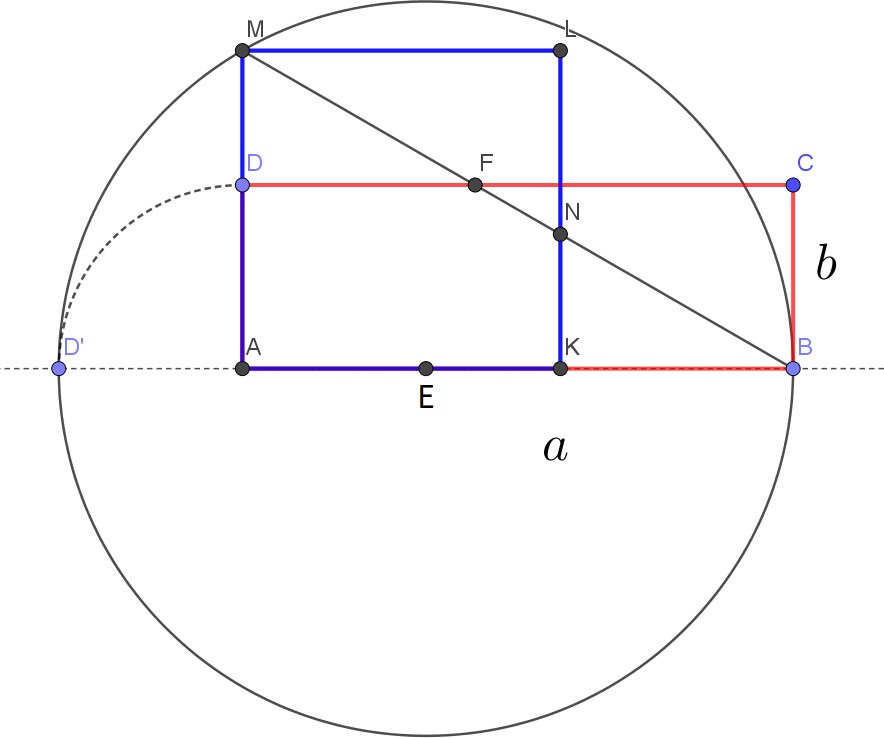
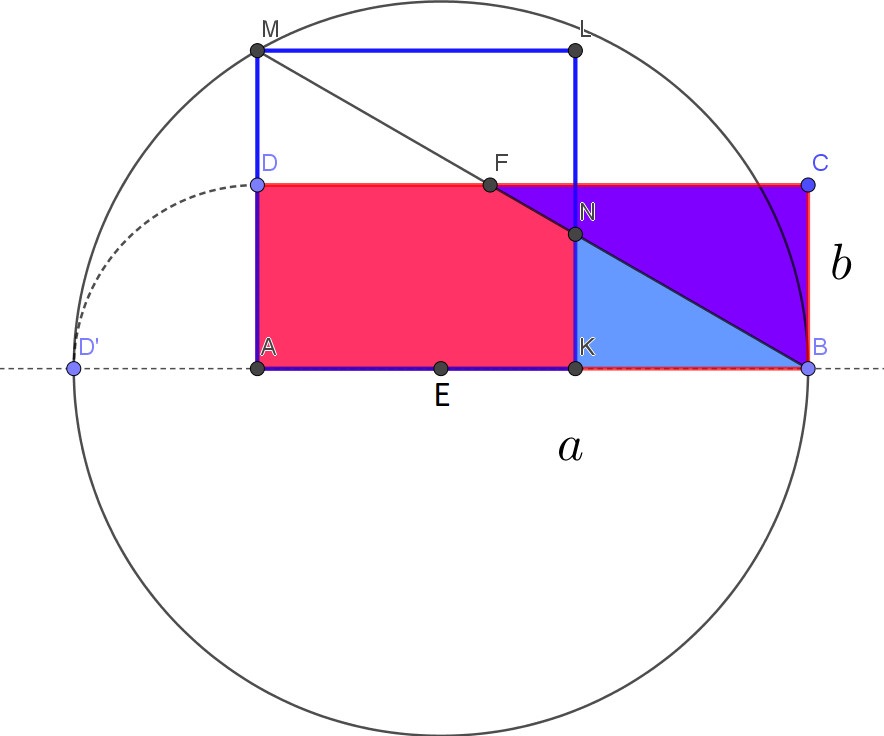
Poruszając suwakiem na Aplecie 3 przesuwamy odpowiednie trójkąty uzyskując poszukiwany kwadrat.

Czy istnieje prostokąt o tym samym polu co kwadrat, którego nie da się przekształcić w ten sposób? Oznaczmy długością c odcinek KN i przyjrzyjmy się rysunkom poniżej.

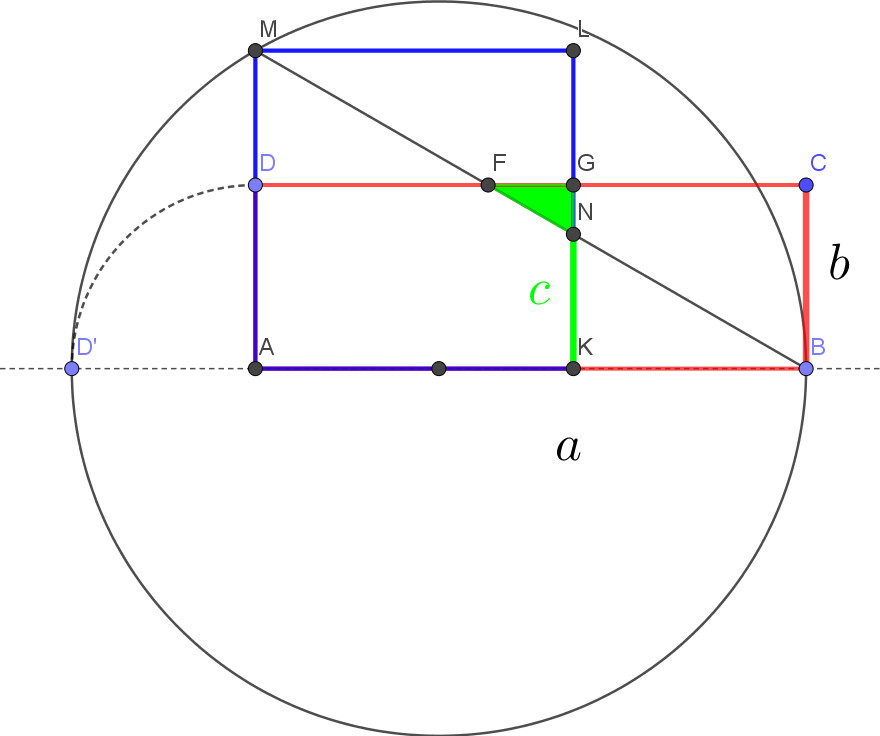
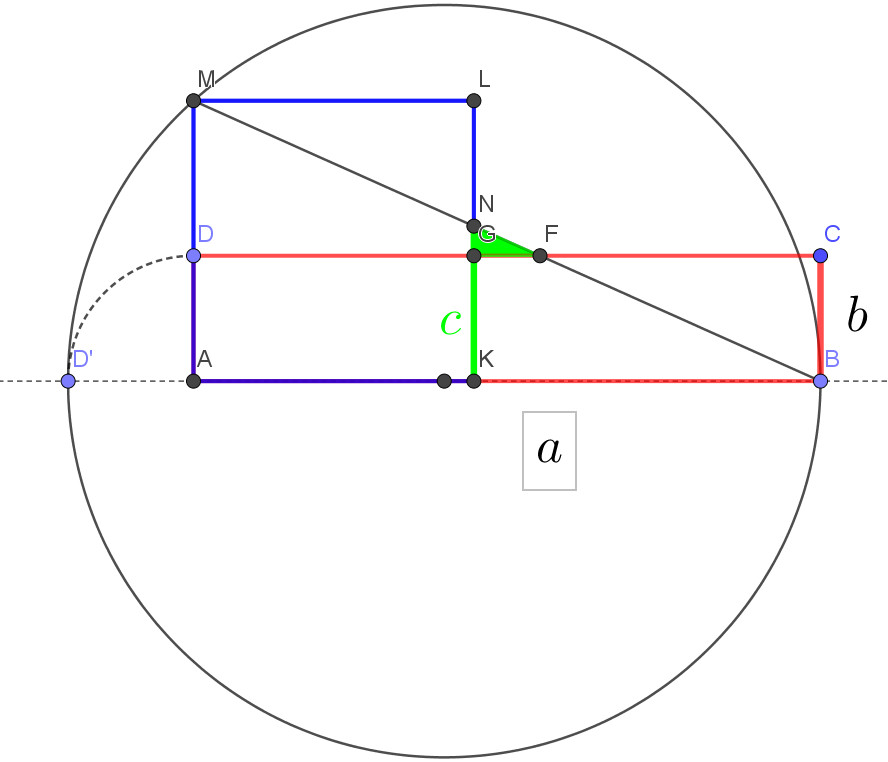
Na Rys. 9 dostrzegamy, że c < b, a zaznaczony zielony trójkąt NGF znajduje się w obrębie kwadratu i prostokąta. Na Rys. 10 c > b i z tego powodu trójkąt NGF znajduje się poza obrębem kwadratu i prostokąta. W takiej sytuacji nie uda nam się przekształcić prostokąta w dany kwadrat. Od czego zależy pozycja naszego trójkąta?

Z podobieństwa trójkątów KBN i ABM wynika: KN AM = KB AB c √ab = a-√ab a c = a√ab - ab a = √ab - b gdy: c ≤ b √ab - b ≤ b √ab≤ 2b | ² ab ≤ 4b² | b a ≤ 4b a b ≤ 4

Zatem, jeżeli prostokąt nie spełnia powyższego warunku nie da się przekształcić go w kwadrat. W przeciwnym wypadku zwiększamy jego wysokość (wzrasta długość b) kosztem szerokości (maleje a ).

Pokazaliśmy, że każdy wielokąt da się rozciąć na pewną ilość kwadratów, których suma pól jest równa polu wielokąta. Kwadraty te potrafimy „zsumować” w opisany wcześniej sposób ( Aplet 1 ). Tak więc każdy wielokąt da się zamienić na kwadrat takim samym polu.

Opisany powyżej problem postawił William Wallace w 1807 roku, a w 1835 roku, rozwiązał Węgier Farkas Bolyai (ojciec Janosa Bolyai, twórcy geometrii hiperbolicznej) wraz z austriackim oficerem Paulem Gerwienem. Na cześć odkrywców, twierdzenie zwane jest twierdzeniem Wallace-Bolyai-Gerwiena.

Inaczej mówiąc, jeżeli dwa wielokąty mają równe pola to każdy z nich można sprowadzić przez opisaną transformację do dwóch kwadratów o tym samym polu.

Problem transformacji w trzecim wymiarze

Czy da się przenieść podobny tok rozumowania do geometrii trójwymiarowej? Skoro dwa wielokąty o tych samych polach możemy rozciąć jeden z nich i złożyć go w drugi, to czy mając dwa, dowolne wielościany o tych samych objętościach, możemy rozciąć jeden z nich tak aby uzyskać drugi.

W 1822 roku podczas posiedzenia Wydziału Matematyczno – Przyrodniczego Akademii Umiejętności w Krakowie, Władysław Kretkowski (1840-1910) postawił zadanie o następującej treści: Mając dane dwa czworościeny równej objętości, zresztą najogólniejsze, pociąć, jeżeli się da to wykonać, płaszczyznami jeden z nich na najmniejszą możliwą liczbę kawałków takich, aby przez stosowne tych kawałków zestawienie, można było zbudować czworościen drugi. W razie, gdyby to dokonać się nie dało, lub było możliwym pod pewnymi zastrzeżeniami dowieść niemożności, lub też zastrzeżenia te dokładnie określić. Kretkowski wyznaczył nagrodę 500 franków dla osoby, która dowiedzie problemu. Dokonał tego Ludwig Birkenmajer (1855-1929), który dowiódł, że zadanie nie ma rozwiązania w pewnych sytuacjach.

Problem ten stał się problemem międzynarodowym, kiedy w 1900 roku w Paryżu, niemiecki matematyk David Hilbert podczas swojego wystąpienia na konferencji matematycznej, przedstawił listę problemów matematycznych, z którymi w niedalekiej przyszłości będzie musiał zmierzyć się świat. Z pośród 23 problemów, na pozycji trzeciej, Hilbert postawił pytanie dotyczące rozkładu wielościanów o jednakowej objętości: Czy mając dane dwa wielościany o równej objętości, można zawsze rozłożyć jeden z nich na skończoną liczbę wielościennych części, a następnie złożyć je w drugi? Hilbert podejrzewał, że nie. Jego słuszność potwierdził, niedługo później, jeden z jego studentów Max Dehn, który podał kontrprzykład, i wprowadzając pojęcie zwane współczynnikiem Dehna, odkrył warunek na to by rozciąć wielościan na inny wielościan o tej samej objętości.