Moduł VI
- Wszystkie ładunki są wielokrotnością ładunku elementarnego e = 1.6·10−19 C.
- Prawo Coulomba opisuje siłę wzajemnego oddziaływania dwóch ładunków
 , gdzie stała
, gdzie stała 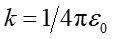 ,
ε0 = 8.854·10−12 C2/(Nm2).
,
ε0 = 8.854·10−12 C2/(Nm2).
- Natężenie pola elektrycznego definiujemy jako siłę działającą na ładunek próbny q
(umieszczony w danym punkcie przestrzeni) podzieloną przez ten ładunek
 .
Natężenie pola elektrycznego E w odległości r od
ładunku punktowego Q jest równe
.
Natężenie pola elektrycznego E w odległości r od
ładunku punktowego Q jest równe  .
.
- Strumień pola elektrycznego przez elementarną powierzchnię dS definiujemy jako iloczyn skalarny
wektora powierzchni dS i natężenia pola elektrycznego E,
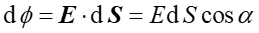 ,
gdzie α jest kątem pomiędzy wektorem
powierzchni dS i wektorem E.
,
gdzie α jest kątem pomiędzy wektorem
powierzchni dS i wektorem E.
- Z prawo Gaussa wynika, że całkowity strumień pola elektrycznego przez zamkniętą powierzchnię jest równy
całkowitemu ładunkowi otoczonemu przez tę powierzchnię podzielonemu przez
ε0
 .
.
- Wypadkowy ładunek wewnątrz przewodnika jest równy zeru; cały ładunek gromadzi się na powierzchni przewodnika.
- Pole elektryczne na zewnątrz naładowanej kuli jest takie jakby cały ładunek skupiony był w środku kuli.
- Ładunek liniowy wytwarza wokół siebie pole malejące wraz z odległością
 .
Natomiast pole od naładowanej nieskończonej płaszczyzny
.
Natomiast pole od naładowanej nieskończonej płaszczyzny  jest
stałe.
jest
stałe.
- Potencjał elektryczny jest zdefiniowany jako energię potencjalna na jednostkowy ładunek
 .
Potencjał ładunku punktowego
.
Potencjał ładunku punktowego
wynosi  .
.
- Energia potencjalna w polu ładunku
punktowego jest dana wzorem
 .
.
- Potencjał elektryczny jest zdefiniowany jako energię potencjalna na jednostkowy
ładunek
 .
Potencjał ładunku punktowego wynosi
.
Potencjał ładunku punktowego wynosi  .
.
- Związek pomiędzy natężeniem pola i potencjałem jest wyrażony zależnością
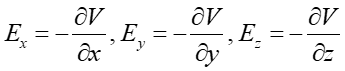 .
.
- Pojemność kondensatora definiujemy jako stosunek ładunku kondensatora do różnicy potencjałów między
okładkami
 .
.
- Energia potencjalna zgromadzona w kondensatorze wynosi
 ,
a gęstość energii pola elektrycznego jest równa
,
a gęstość energii pola elektrycznego jest równa  .
.
- Umieszczenie dielektryka o względnej przenikalności elektrycznej εr
pomiędzy okładkami kondensatora zwiększa jego pojemność εr
razy
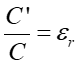 .
.
 , gdzie stała
, gdzie stała 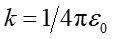 ,
ε0 = 8.854·10−12 C2/(Nm2).
,
ε0 = 8.854·10−12 C2/(Nm2). .
Natężenie pola elektrycznego E w odległości r od
ładunku punktowego Q jest równe
.
Natężenie pola elektrycznego E w odległości r od
ładunku punktowego Q jest równe  .
. 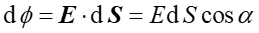 ,
gdzie α jest kątem pomiędzy wektorem
powierzchni dS i wektorem E.
,
gdzie α jest kątem pomiędzy wektorem
powierzchni dS i wektorem E.  .
.  .
Natomiast pole od naładowanej nieskończonej płaszczyzny
.
Natomiast pole od naładowanej nieskończonej płaszczyzny  jest
stałe.
jest
stałe.  .
Potencjał ładunku punktowego
.
Potencjał ładunku punktowego .
.  .
.  .
Potencjał ładunku punktowego wynosi
.
Potencjał ładunku punktowego wynosi  .
. 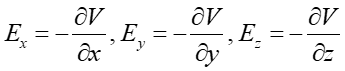 .
.  .
.  ,
a gęstość energii pola elektrycznego jest równa
,
a gęstość energii pola elektrycznego jest równa  .
. 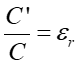 .
. 

 Kondensator z dielektrykiem
Kondensator z dielektrykiem