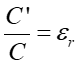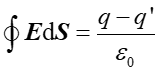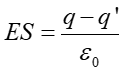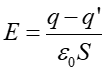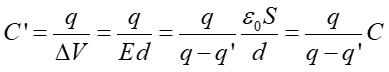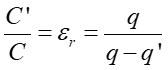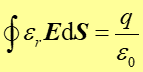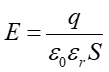Kondensator z dielektrykiem

20.3 Kondensator z dielektrykiem

Doświadczenie pokazuje, że umieszczenie dielektryka (izolatora) pomiędzy okładkami kondensatora zwiększa jego pojemność ε_r razy

(20.11)

Wielkość ε_r nazywamy względną przenikalnością elektryczną lub stałą dielektryczną . W tabeli poniżej zestawione zostały stałe dielektryczne wybranych materiałów

Tab. 20.1. Stałe dielektryczne wybranych materiałów (w temperaturze pokojowej)

Ośrodek	ε_r
próżnia	1
powietrze	1.0006
parafina	2
teflon	2.1
polietylen	2.3
papier	3.5
szkło (pyrex)	4.5
porcelana	6.5
woda	81
TiO₂	100

Wzrost pojemności kondensatora w wyniku umieszczenia w nim dielektryka wynika z zachowania się atomów (cząsteczek) dielektryka w polu elektrycznym w kondensatorze, przy czym istnieją dwie możliwości.

Po pierwsze istnieją cząsteczki, w których środek ładunku dodatniego jest trwale przesunięty względem środka ładunku ujemnego. Przykładem może być cząsteczka H₂O pokazana na rysunku poniżej.

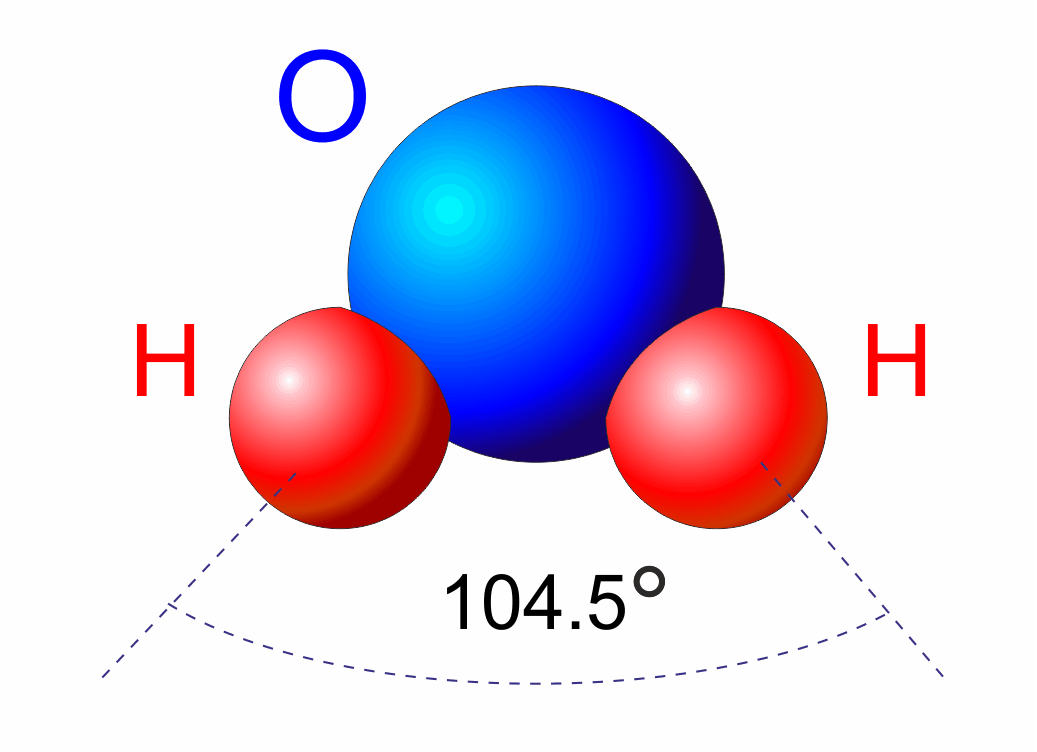
Rys. 20.2. Cząsteczka wody charakteryzującą się trwałym momentem dipolowym

W wyniku charakterystycznej budowy w cząsteczce wody ładunek ujemny jest przesunięty w stronę atomu tlenu, a środek ładunku dodatniego jest bliżej atomów wodoru. Takie cząsteczki mają więc trwały elektryczny moment dipolowy.

Po drugie, w przypadku cząsteczek i atomów nie posiadających trwałych momentów dipolowych taki moment może być wyindukowany przez umieszczenie ich w zewnętrznym polu elektrycznym. Pole działa na ładunki dodatnie (jądra atomowe) i ujemne (chmury elektronowe) rozsuwając ich środki. Atomy (cząsteczki) wykazują elektryczny moment dipolowy, ulegają polaryzacji . Przykładowo, jeżeli umieścimy atom wodoru w zewnętrznym polu E, to siła F = −eE przesuwa elektron o r względem protonu. Wówczas atom ma indukowany moment dipolowy p = er. Ponieważ jest to moment indukowany polem zewnętrznym więc znika, gdy usuniemy pole.

W zerowym polu momenty dipolowe są zorientowane przypadkowo tak jak pokazano na rysunku 20.3a. Natomiast po umieszczeniu w polu elektrycznym trwałe elektryczne momenty dipolowe dążą do ustawienia zgodnie z kierunkiem pola, a stopień uporządkowania zależy od wielkości pola i od temperatury (ruchy termiczne cząstek zaburzają uporządkowanie). Natomiast momenty indukowane są równoległe do kierunku pola. Cały materiał w polu E zostaje spolaryzowany. Spolaryzowany zewnętrznym polem E dielektryk (umieszczony w naładowanym kondensatorze) jest pokazany na rysunku 20.3b.

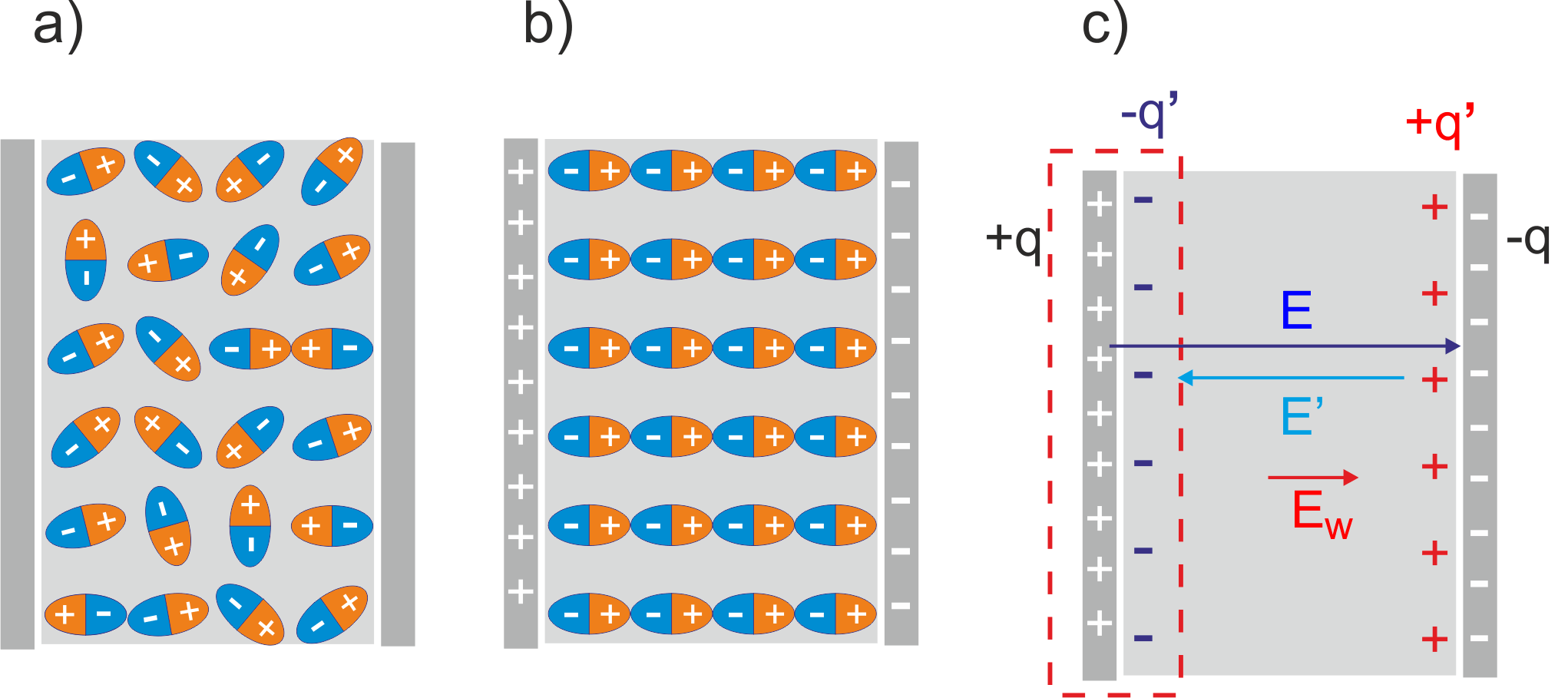
Rys. 20.3. a) niespolaryzowany dielektryk, b) polaryzacja dielektryka w zewnętrznym polu E, c) wypadkowy rozkład ładunku

Zwróćmy uwagę, że w rezultacie wewnątrz dielektryka ładunki kompensują się, a jedynie na powierzchni dielektryka pojawia się nieskompensowany ładunek q'. Ładunek dodatni gromadzi się na jednej, a ujemny na drugiej powierzchni dielektryka tak jak pokazano na rysunku 20.3b.

Ładunek q jest zgromadzony na okładkach, a q' jest ładunkiem wyindukowanym na powierzchni dielektryka. Te wyindukowane ładunki wytwarzają pole elektryczne E ' przeciwne do pola E pochodzącego od swobodnych ładunków na okładkach kondensatora. Wypadkowe pole w dielektryku E_w (suma wektorowa pól E ' i E) ma ten sam kierunek co pole E ale mniejszą wartość. Pole związane z ładunkiem polaryzacyjnym q' nosi nazwę polaryzacji elektrycznej . Widzimy, że

Prawo, zasada, twierdzenie
Gdy umieścimy dielektryk w polu elektrycznym to pojawiają się indukowane ładunki powierzchniowe, które wytwarzają pole elektryczne przeciwne do zewnętrznego pola elektrycznego.

Zastosujemy teraz prawo Gaussa do kondensatora wypełnionego dielektrykiem. Dla powierzchni Gaussa zaznaczonej na rysunku 20.3c linią przerywaną otrzymujemy

(20.12)

Ponieważ pole E jest jednorodne więc

(20.13)

skąd otrzymujemy

(20.14)

Pojemność takiego kondensatora wypełnionego dielektrykiem wynosi zatem

(20.15)

Dzieląc powyższe równanie obustronnie przez C otrzymujemy

(20.16)

Powyższe równanie pokazuje, że wyindukowany ładunek powierzchniowy q' jest mniejszy od ładunku swobodnego q na okładkach. Dla kondensatora bez dielektryka q' = 0 i wtedy ε_r = 1. Więcej o ... o dielektrykach.

Korzystając z powyższego związku, podstawiając za q − q' do równania (20.12), możemy napisać prawo Gaussa (dla kondensatora z dielektrykiem) w postaci

(20.17)

To równanie stanowi najbardziej ogólną postać prawa Gaussa.

Zauważmy, że strumień pola elektrycznego dotyczy wektora ε_rE (a nie wektora E) i że w równaniu występuje tylko ładunek swobodny, a wyindukowany ładunek powierzchniowy został uwzględniony przez wprowadzenie stałej dielektrycznej ε_r.

Porównując pole elektryczne w kondensatorze płaskim bez dielektryka E = q/ε₀S z wartością daną równaniem (20.14) widzimy, że wprowadzenie dielektryka zmniejsza pole elektryczne ε_r razy (indukowany ładunek daje pole przeciwne do pola od ładunków swobodnych na okładkach - rysunek 20.3c).

(20.18)

Ćwiczenie
Pokazaliśmy, że wprowadzenie dielektryka między okładki kondensatora zwiększa jego pojemność i zmniejsza pole elektryczne ε_r razy. Spróbuj teraz wyjaśnić jak zmienia się różnica potencjałów między okładkami i energia naładowanego kondensatora. Zauważ, że ładunek swobodny na okładkach kondensatora nie zmienia się (kondensator został naładowany i następnie odłączony od źródła – baterii). Sprawdź obliczenia i wynik.

Ten rozdział kończy moduł czwarty; możesz teraz przejść do podsumowania i zadań testowych.