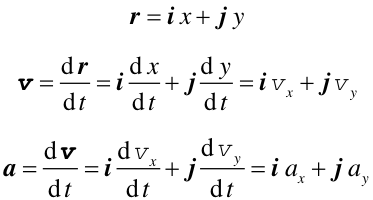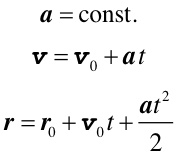Ruch jednowymiarowy, przyspieszenieRuch w dwóch wymiarach będziemy opisywać w układzie współrzędnych x i y. Np. y - wysokość, x - odległość w kierunku poziomym. Pokażemy, że taki ruch można traktować jak dwa niezależne ruchy jednowymiarowe.
3.1 Przemieszczenie, prędkość i przyspieszenie
Położenie punktu w chwili t przedstawia wektor r(t);
prędkość wektor v(t),przyspieszenie wektor a(t).
Wektory r(t), v(t), a(t)
są wzajemnie zależne od siebie i dadzą się przedstawić za pomocą
wersorów 
i, j czyli wektorów jednostkowej długości zorientowanych
odpowiednio wzdłuż osi x i y.
|
(3.1) |
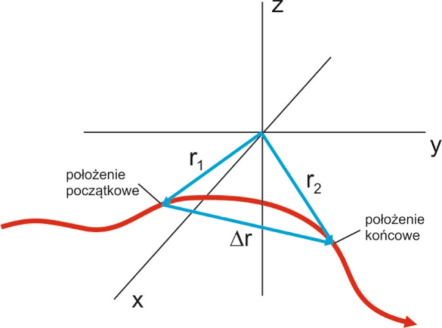
Położenie punktu określić można podając wektor r lub, dla wybranego układu odniesienia, poprzez podanie współrzędnych tego wektora np. x, y.
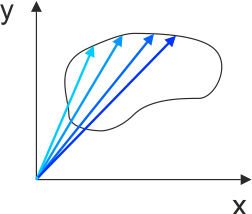
Oczywiście wektor r i jego współrzędne zmieniają się z czasem więc trzeba podać zależności czasowe r(t), x(t), y(t) tak jak na rysunku-animacji poniżej.
|
Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.
|
| Rys. 3.1a. Zmiany wektora położenia z czasem |
|
Warto w tym miejscu również zapamiętać, że wektor prędkości jest zawsze styczny do toru poruszającego się punktu.
Punkty, przez które przechodzi poruszający się punkt tworzą krzywą, którą nazywamy
torem ruchu .
Jako przykład rozpatrzmy ruch jednostajnie zmienny na płaszczyźnie. Ponieważ ruch odbywa się ze stałym przyspieszeniem tzn. nie zmieniają się ani kierunek ani wartość przyspieszenia to nie zmieniają się też składowe przyspieszenia.
Spróbujmy najpierw napisać równania wektorowe dla tego ruchu. Mają one następującą postać
|
(3.2) |
Przypuśćmy, że chcemy znaleźć położenie ciała (wektor r) po czasie t.
Jak widać z równania (3.2) trzeba wyznaczyć (znaleźć wartość, kierunek i zwrot) i dodać do siebie
geometrycznie trzy wektory: r0, v0t
oraz 1/2at2 .
Zadanie możemy jednak znacznie uprościć korzystając z tego, że równania
wektorowe (3.2) są równoważne równaniom w postaci skalarnej (zestawionym
w tabeli 3.1 poniżej) i zamiast dodawania geometrycznego wektorów możemy
po prostu dodawać liczby. Znalezienie wektora r sprowadza się
teraz do znalezienia jego składowych.
Tab. 3.1
| Równania skalarne opisujące ruch wzdłuż osi x | Równania skalarne opisujące ruch wzdłuż osi y |
|---|---|
 |
 |
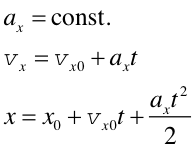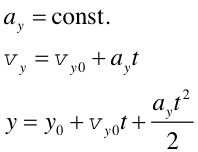Przykładem na którym prześledzimy ruch krzywoliniowy ze stałym przyspieszeniem jest rzut ukośny.