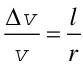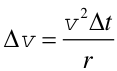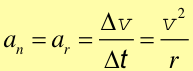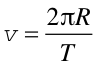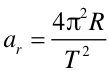Ruch jednostajny po okregu

3.3 Ruch jednostajny po okręgu

Rozważać będziemy ciało poruszające się ze stałą prędkością po okręgu o promieniu R pokazane na rysunku poniżej. Punkt materialny poruszający się jednostajnie po okręgu znajduje się w punkcie P w chwili t, a w punkcie P' w chwili t + Δt. Wektory prędkości v, v' mają jednakowe długości ale różnią się kierunkiem; pamiętajmy, że wektor prędkości jest zawsze styczny do toru. Chcąc znaleźć przyspieszenie musimy wyznaczyć różnicę prędkości v i v'.

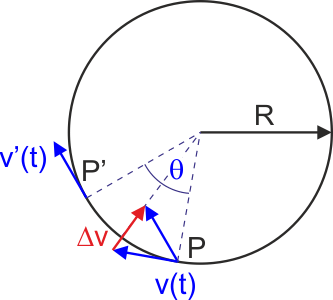
Rys. 3.4. Ruch jednostajny po okręgu

W tym celu przerysowujemy wektor v' w punkcie P i wyznaczamy różnicę Δv. Zauważmy, że kąt pomiędzy wektorami v i v' jest równy kątowi θ więc korzystając z podobieństwa trójkątów możemy zapisać równość

(3.12)

gdzie l jest długością odcinka PP', a dla małych wartości l z dobrym przybliżeniem długością łuku PP'.

Ponieważ l = v Δt więc

(3.13)

Znając już Δv możemy obliczyć przyspieszenie

(3.14)

Jak widać na rysunku 3.4, wektor Δv jest prostopadły do toru to znaczy pokrywa się z kierunkiem promienia i jest zwrócony do środka okręgu. Oznacza to, że i wektor przyspieszenia ma taki sam kierunek i zwrot (rysunek-animacja 3.5). W ruchu po okręgu przyspieszenie to nazywamy przyspieszeniem dośrodkowym (jest zwrócone do środka okręgu), a dla ruchu po dowolnej krzywej przyspieszeniem normalnym a_n (jest prostopadłe do toru) lub radialnym a_r(jest skierowane wzdłuż promienia).
Przyspieszenie normalne jest związane ze zmianą kierunku prędkości, a przyspieszenie styczne za zmianę jej wartości.

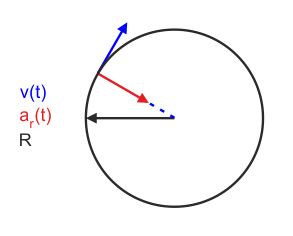
Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.

Rys. 3.5. Ruch jednostajny po okręgu

Przyspieszenie dośrodkowe często wyraża się poprzez okres T czyli czas, w którym punkt materialny wykonuje pełen obieg okręgu. Ponieważ

(3.15)

więc

(3.16)

Ćwiczenie
Korzystając z powyższego wyrażenia spróbuj obliczyć jakiego przyspieszenia wynikającego z obrotu Ziemi, doznaje ciało będące na równiku? Załóż, że Ziemia jest kulą o promieniu R_Z = 6370 km. Jak duże jest to przyspieszenie w porównaniu do przyspieszenia grawitacyjnego g = 9.81 m/s² ? Sprawdź obliczenia i wynik.

Na zakończenie rozważań dotyczących ruchu na płaszczyźnie jeszcze raz zajmiemy się rzutem ukośnym jako przykładem ruchu krzywoliniowego.