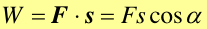7. Praca i energia
• Spis treści  
• Praca wykonana przez siłę zmienną  
•   Test

   Znajomość zagadnień związanych z szeroko rozumianym pojęciem energii jest konieczna dla wszelkich rozważań zarówno technologicznych, ekonomicznych, ekologicznych jak i społecznych. Żeby się o tym przekonać wystarczy sprawdzić jak istotną pozycją w budżecie domowym stanowią wydatki związane z zapotrzebowaniem na energię (zakupy żywności, opłaty za prąd, gaz, ogrzewanie czy paliwo do samochodu).
Z energią związana jest najważniejsza chyba zasada całej fizyki - zasada zachowania energii. Nakłada ona sztywne granice na przetwarzanie energii i jej wykorzystanie. Do zasady tej będziemy się odwoływali wielokrotnie w kolejnych rozdziałach dotyczących różnych zagadnień fizyki.
W mechanice zasada zachowania energii pozwala obliczać w bardzo prosty sposób ruch ciał, stanowi alternatywę do stosowania zasad dynamiki Newtona.

7.1 Praca wykonana przez siłę stałą

   W najprostszym przypadku, punkt materialny przemieszcza się pod wpływem stałej siły F. Traktując przesunięcie s jako wektor o długości równej drodze jaką przebywa ten punkt i kierunku zgodnym z kierunkiem ruchu, możemy zdefiniować pracę W.

gdzie α jest kątem między kierunkami siły i przesunięcia. Zwróćmy uwagę, że kąt α może być różny od zera bo stała siła nie musi mieć kierunku zgodnego z kierunkiem ruchu punktu materialnego. Dzieje się tak gdy działają jeszcze inne siły (np. ciężar, tarcie). Ale nawet gdy działała tylko jedna siła to i tak ciało nie musi poruszać się w kierunku jej działania np. siła grawitacji w rzucie ukośnym. Rozpatrzmy teraz następujący przykład.

Przykład

Ciało o masie m ( na przykład sanki) jest ciągnięte po poziomej powierzchni stałą siłą F (rysunek poniżej), a sznurek, za który ciągniemy tworzy kąt α z poziomem. Praca jaką wykonał człowiek ciągnący to ciało na drodze s jest zgodnie z równaniem (7.1) równa Fscosα. Zauważmy, że pracę wykonuje tylko składowa F_s = F cosα styczna do przesunięcia s. Natomiast składowa pionowa Fsinα działa w górę zmniejszając nacisk ciała na powierzchnię.

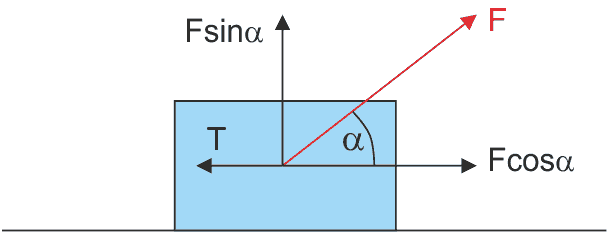
 Rys. 7.1. Ciało o masie m ciągnięte po poziomej powierzchni stałą siłą F  tworzącą kąt α z poziomem

Ze wzoru (7.1) wynika, że praca może przyjmować zarówno wartości dodatnie gdy α < 90°, jak i ujemne gdy  α > 90°. W omawianym przykładzie, poza siłą ciągnącą ciało, działa jeszcze siła tarcia kinetycznego T (rysunek 7.1) przeciwstawiająca się ruchowi (α = 180°). Praca wykonana przez siłę tarcia jest ujemna
W = T·s = Ts cos180° = −Ts. W szczególności praca może być równa zeru, gdy kierunek siły jest prostopadły do kierunku przesunięcia (α  = 90°, cos90° = 0). Przykładem może być siła dośrodkowa. Przyspieszenie dośrodkowe jest prostopadłe do toru więc siła dośrodkowa nie wykonuje pracy.

Rozpatrzmy jeszcze raz powyższy przykład ale w sytuacji gdy człowiek ciągnący ciało porusza się ze stałą prędkością. Z pierwszej zasady dynamiki wynika, że wtedy F_wyp = 0. W kierunku poziomym F_wyp = Fcos α − T = 0, zatem "dodatnia" praca wykonana przez człowieka jest równa co do wartości bezwzględnej "ujemnej" pracy wykonanej przez siłę tarcia.

Z podobna sytuacją mamy do czynienia przy podnoszeniu w górę (ze stałą prędkością) ciała o masie m na wysokość h (rysunek - animacja 7.2 obok). Zauważmy, że w trakcie podnoszenia ciała człowiek działa siłą F równą ciężarowi ale przeciwnie skierowaną, więc "dodatnia" praca W = mgh wykonana na drodze h przez siłę F (człowieka) jest równa co do wartości  "ujemnej" pracy wykonanej przez siłę ciężkości. Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.  Rys. 7.2. Podnoszenie ciężaru na wysokość

Teraz gdy znasz już definicję pracy spróbuj samodzielnie odpowiedzieć na proste pytania związane z następującym ćwiczeniem:

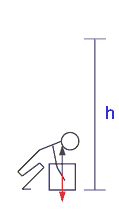
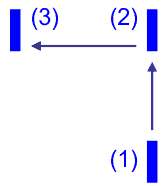
Ćwiczenie Wyobraź sobie, że podnosisz książkę na półkę, tak jak pokazano to na rysunku obok. W pierwszym kroku podnosisz książkę z położenia (1) i umieszczasz ją na półce (położenie 2). Następnie przenosisz książkę poziomo ze stałą prędkością na inne miejsce na półce (położenie 3). Jaki znak ma praca wykonana przez ciebie na odcinku 1-2 i 1-3, a jaki znak ma praca wykonana przez siłę ciężkości?  Tarcie i wszelkie opory pomijamy.

Wzór (7.1) pozwala obliczyć pracę dla siły stałej; do obliczeń "podstawiamy" za F konkretną jej wartość. Teraz poznamy jak obliczyć  pracę gdy siła zmienia się, przyjmuje różne wartości.