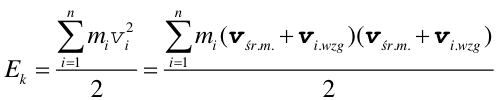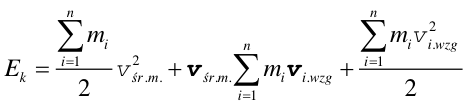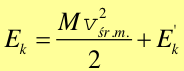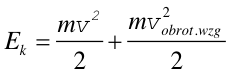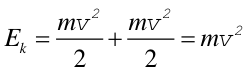Energia kinetyczna w układzie środka masy

Rozpatrzmy układ, o stałej masie M, złożony z n punktów materialnych o masach m₁, ......, m_n oraz prędkościach v₁, ....., v_n. Energia kinetyczną tego układu mierzone względem środka masy jest dana wyrażeniem

(1)

gdzie v_śr.m. jest prędkością środka masy, a v_i,wzg jest prędkością i-tego punktu mierzoną w układzie środka masy. Wykonując mnożenie skalarne otrzymujemy

(2)

Zgodnie z równaniem (9.6) 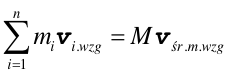, a ponieważ prędkość środka masy mierzona względem środka masy jest równa zeru
V_śr.m.,wzg = 0 więc drugi wyraz w równaniu (2) znika. Ostatecznie

(3)

gdzie E_k' jest energią kinetyczną mierzoną w układzie środka masy. Zastosowanie tego równania zilustrujemy następującym przykładem:

Przykład

Obliczmy energię kinetyczną obręczy o masie m toczącej się po płaszczyźnie tak, że środek obręczy ma prędkość v (rysunek poniżej).

Rys. 1. Obręcz tocząca się bez poślizgu z prędkością v

Ponieważ w układzie środka masy ciało sztywne może mieć tylko energię obrotową (rotacyjną ) więc równanie (3) przyjmuje postać

(4)

gdzie v_obrot,wzg to prędkość obręczy w układzie środka masy. Ponieważ obserwator w układzie środka masy widzi obręcz obracającą się z prędkością v więc v_obrot,wzg = v. Stąd

(5)

Zauważmy, że obręcz ma energię dwa razy większą od ciała o masie m poruszającego się z tą samą prędkością v (ale nie obracającego się).