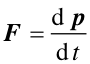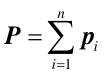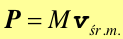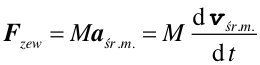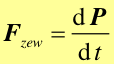Ruch środka masy9.3 Pęd układu punktów materialnych
Zdefiniowaliśmy pęd punktu materialnego jako iloczyn jego masy m i jego prędkości v. Poznaliśmy też, drugą zasadę dynamiki Newtona w postaci
|
(9.10) |
Jeżeli jednak zamiast pojedynczego punktu mamy do czynienia z układem, o stałej masie M, złożonym z n punktów materialnych o masach m1, ......, mn oraz prędkościach v1, ....., vn to układ jako całość będzie miał całkowity pęd P będący sumą wektorową pędów poszczególnych punktów
|
(9.11) |
Porównując tę zależność z równaniem (9.6) 
otrzymujemy zależność
|
(9.12) |
|
Prawo, zasada, twierdzenie Całkowity pęd układu punktów materialnych jest równy iloczynowi całkowitej masy układu i prędkości jego środka masy. |
Zgodnie z równaniem (9.7)
|
(9.13) |
więc druga zasada dynamiki Newtona dla układu punktów materialnych przyjmuje postać
|
(9.14) |
Ponownie widzimy, że nawet ciała materialne będące układami złożonymi z dużej liczby punktów materialnych możemy w pewnych sytuacjach traktować jako pojedynczy punkt materialny. Tym punktem jest środek masy.
Z równania (9.14) wynika, że gdy wypadkowa siła zewnętrzna równa jest zeru Fzew = 0, to dla układu o stałej masie, środek masy pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, przy czym poszczególne punkty układu mogą poruszać się po różnych torach.
To stwierdzenie wprowadza nas w zasadę zachowania pędu.