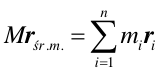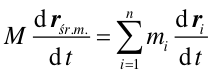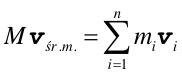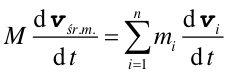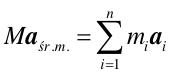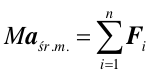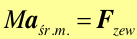Ruch środka masy

9.2 Ruch środka masy

Rozważmy układ punktów materialnych o masach m₁, m₂, m₃ ..., m_n i o stałej całkowitej masie M. Na podstawie równania (9.4) możemy napisać

(9.5)

Różniczkując (względem czasu) powyższe równanie otrzymujemy zgodnie z równaniami (3.1)

(9.6)

a po ponownym różniczkowaniu

(9.7)

To ostatnie równanie możemy zapisać w postaci

(9.8)

Suma (wektorowa) wszystkich sił działających na poszczególne punkty materialne układu jest równa wypadkowej sile zewnętrznej więc

(9.9)

Z równania (9.9) wynika, że

Prawo, zasada, twierdzenie
Środek masy układu punktów materialnych porusza się w taki sposób, jakby cała masa układu była skupiona w środku masy i jakby wszystkie siły zewnętrzne nań działały.

Z twierdzenia o ruchu środka masy wynika, że nawet ciała materialne będące układami złożonymi z dużej liczby punktów materialnych możemy w pewnych sytuacjach traktować jako pojedynczy punkt materialny. Tym punktem jest środek masy.
To twierdzenie obowiązuje dla każdego układu punktów materialnych. W szczególności układ może być ciałem o budowie ciągłej (np. ciało stałe). Wtedy przy obliczeniach środka masy sumowanie występujące w równaniach (9.3), (9.4) zastępujemy całkowaniem. Układ może też być zbiorem cząstek, w którym występują wszystkie rodzaje ruchu wewnętrznego.

Pojęcie środka masy jest bardzo użyteczne np. do obliczania energii kinetycznej Więcej o ...