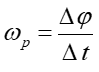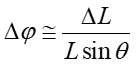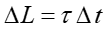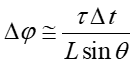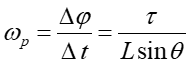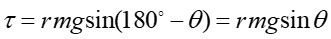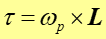Ruch precesyjny

Inny przykładem ruchu obrotowego, w którym oś obrotu nie jest nieruchomą w inercjalnym układzie odniesienia jest bąk wirujący dookoła pewnej osi symetrii. Z doświadczenia wiemy, że oś wirującego bąka porusza się dookoła osi pionowej, zakreślając powierzchnię stożka. Taki ruch nazywamy
precesją .

W sytuacji przedstawionej na rysunku poniżej bąk ma prędkość kątową ω dookoła swej osi. Ma również moment pędu L względem tej osi, która tworzy kąt θ z osią pionową. Punkt podparcia bąka znajduje się w początku inercjalnego układu odniesienia.

Rys. 1 Ruch precesyjny bąka

Siła działająca na bąk w punkcie podparcia ma zerowy moment względem punktu podparcia ponieważ ramię siły jest równe zeru. Natomiast ciężar mg wytwarza względem punktu podparcia moment siły

(1)

gdzie r określa położenie środka masy. Z iloczynu wektorowego wynika, że τ jest prostopadłe do r i do mg. Zauważmy, że wektory τ , L i r wirują dokoła osi pionowej z częstością precesji ω_p. Z rysunku wynika, że

(2)

Ponieważ ΔL << L, to możemy napisać

(3)

Z drugiej zasadę dynamiki ruchu obrotowego równanie (11.11) wynika, że

(4)

więc

(5)

Ostatecznie otrzymujemy

(6)

Zgodnie z rysunkiem 1 moment siły jest równy

(7)

więc ostatecznie

(8)

Zwróćmy uwagę, że prędkość precesji nie zależy od kąta θ i jest odwrotnie proporcjonalna do wartości momentu pędu.

Spróbujmy teraz podać ogólne wektorowe równanie opisujące precesję. W tym celu najpierw przekształcamy równanie (6) do postaci

(9)

Widać, że prawa strona równania jest równa wartości iloczynu wektorowego ω_p x L. Tak więc ostatecznie wyrażenie wiążące prędkość kątową precesji z momentem siły i momentem pędu ma postać

(10)

Zjawisko precesji momentu magnetycznego jest podstawą różnych technik doświadczalnych jak np. magnetyczny rezonans jądrowy (MRJ), które znalazły szerokie zastosowanie w badaniach naukowych, technice i medycynie.