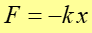12. Ruch drgający
• Spis treści  
• Wahadła  
•   Ruch obrotowo-postępowy

  Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym. Przemieszczenie cząstki w ruchu periodycznym można zawsze wyrazić za pomocą funkcji sinus lub cosinus (tzw. funkcji harmonicznych). Ruch drgający jest powszechną formą ruchu obserwowaną w życiu codziennym i dlatego jest ważnym przedmiotem fizyki.

12.1 Siła harmoniczna, drgania swobodne

Dla przesunięcia wzdłuż osi x, siła sprężystości jest dana równaniem

gdzie x jest wychyleniem (przesunięciem) ciała od położenia równowagi. Stałą k nazywamy współczynnikiem sprężystości . Z siłą harmoniczną (sprężystości) spotkaliśmy się już w poprzednich rozdziałach (7.2 i 8.3) gdy rozważaliśmy siłę związaną z rozciąganiem sprężyny i elastycznej liny. W animacji 12.1 pokazane jest ciało o masie m przymocowane do sprężyny, mogące poruszać się bez tarcia po poziomej powierzchni. Takie  drgania, gdy siła sprężystości jest zarazem siłą wypadkową nazywamy drganiami swobodnymi .

Kliknij w dowolnym miejscu na rysunku żeby uruchomić animację. Ponowne kliknięcie oznacza powrót do początku.

 Rys. 12.1. Prosty oscylator harmoniczny

Jeżeli sprężyna zostanie rozciągnięta tak, aby masa m znalazła się w chwili t = 0 w położeniu x = A, (rysunek 12.1), a następnie zostanie zwolniona, to położenie masy w funkcji czasu może być dane równaniem

Funkcja x(t) opisuje zarazem wychylenie ciała z położenia równowagi. Sprawdźmy teraz czy to równanie dobrze opisuje ruch harmoniczny. Zgodnie z drugą zasadą dynamiki Newtona

Żeby obliczyć przyspieszenie a obliczamy odpowiednie pochodne równania (3.1)

Teraz wyrażenia (12.2) i (12.5) podstawiamy do równania opisującego ruch oscylatora (12.3) i otrzymujemy

Widzimy, że zaproponowane równanie (12.2) jest rozwiązaniem równania ruchu oscylatora harmonicznego (12.3) przy warunku, że (równanie 12.6).

Zwróćmy uwagę, że funkcja   jest również rozwiązaniem równania ale przy innych warunku początkowym bo gdy t = 0 to położenie masy x = 0, a nie jak przyjęliśmy x = A.

Ogólne rozwiązanie równania ruchu oscylatora harmonicznego (12.3) ma postać

Stała A (opisująca maksymalne wychylenie) jest amplitudą ruchu , wyrażenie ωt + φ nazywamy fazą drgań , a φ fazą początkową (stałą fazową). Stałe  A i φ są wyznaczone przez warunki początkowe. Np. dla φ = π/2 otrzymujemy rozwiązanie (12.2).

Równania (12.2), (12.4) i (12.5) opisują kolejno położenie, prędkość i przyspieszenie w funkcji czasu. Zależności te są pokazane na rysunku 12.2.

 Rys. 12.2. Wykres zależności x(t), v(t), a(t) dla prostego ruchu harmonicznego

Zwróćmy uwagę, że wychylenie z położenia równowagi x(t) oraz przyspieszenie a(t) (a tym samym siła) osiągają równocześnie maksymalne wartości, przy czym zwroty wektorów x(t) i a(t) są przeciwne (równanie (12.3) i stąd przeciwne znaki. Natomiast prędkość v(t) jest przesunięta w fazie (względem położenia) o π/2 co odzwierciedla fakt, że prędkość osiąga maksimum przy przechodzeniu oscylującej masy przez położenie równowagi, a jest zerowa przy maksymalnym wychyleniu gdy ciało zawraca (animacja 12.1). Odpowiednie maksymalne wartości położenia, prędkości i przyspieszenia wynoszą

Wartości funkcji sinus i cosinus powtarzają się gdy kąt zmienia się o 2π. Oznacza to, że funkcje x(t) v(t) i a(t)  przyjmują taką samą wartość po czasie t = 2π/ω. Ten czas jest więc okresem ruchu T. Uwzględniając zależność (12.6) otrzymujemy

Zwróćmy uwagę, że okres drgań harmonicznych T jest niezależny od amplitudy drgań A. Ta właściwość drgań harmonicznych została wykorzystana w konstrukcji zegara wahadłowego.

 Więcej o ...  układach drgających (drgania dwu ciał).