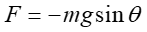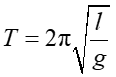Wahadła

12.2 Wahadła

Wahadło proste

Wahadło proste (matematyczne) jest to wyidealizowane ciało o masie punktowej, zawieszone na cienkiej, nieważkiej, nierozciągliwej nici. Kiedy ciało wytrącimy z równowagi to zaczyna się ono wahać w płaszczyźnie poziomej pod wpływem siły ciężkości. Jest to ruch okresowy. Znajdźmy okres T tego ruchu. Rysunek 12.3 przedstawia wahadło o długości l i masie m, odchylone o kąt θ od pionu. Na masę m działa siła grawitacji mg i naprężenia nici N.

Rys. 12.3. Wahadło matematyczne

Siłę mg rozkładamy na składową radialną (normalną) i styczną. Składowa normalna jest równoważona przez naciąg nici N. Natomiast składowa styczna przywraca równowagę układu i sprowadza masę m do położenia równowagi. Składowa ta ma wartość

(12.10)

Zwróćmy uwagę, że to nie jest, w myśl podanej definicji, siła harmoniczna bo jest proporcjonalna do sinusa wychylenia (sinθ), a nie do wychylenia θ. Jeżeli jednak kąt θ jest mały (np. 5°) to sinθ jest bardzo bliski θ (różnica ≈ 0.1%). Przemieszczenie x wzdłuż łuku wynosi (z miary łukowej kąta) x = lθ. Przyjmując zatem, że sinθ ≈ θ otrzymujemy

(12.11)

Tak więc dla małych wychyleń siła jest proporcjonalna do przemieszczenia i mamy do czynienia z ruchem harmonicznym. Równanie (12.11) jest analogiczne do równania równania (12.1) przy czym k = mg/l. Możemy więc skorzystać z zależności (12.9) i obliczyć okres wahań

(12.12)

Okres wahadła prostego nie zależy od amplitudy i od masy wahadła.

Symulacje komputerowe
Korzystając z załączonego programu możesz prześledzić ruch wahadła matematycznego w zależności od jego długości. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera.

Zauważmy, że pomiar okresu T może być prostą metodą wyznaczenia przyspieszenia g.

Ćwiczenie
Spróbuj wykonać takie doświadczenie. Na nitce (możliwie długiej np. 1.5 m) zawieś niewielki ciężarek. Następnie wychyl wahadło o niewielki kąt (żeby było spełnione kryterium ruchu harmonicznego) i zmierz okres wahań. Żeby zmniejszyć błąd pomiaru czasu zmierz okres kilku wahań (np. 10) i potem oblicz T. Ze wzoru (12.12) wylicz przyspieszenie g.

Wahadło fizyczne

Wahadłem fizycznym nazywamy ciało sztywne zawieszone tak, że może się wahać wokół pewnej osi przechodzącej przez to ciało. Ciało jest zawieszone w punkcie P, a punkt S, znajdujący się w odległości d od punkt P, jest środkiem masy ciała (rysunek 12.4).

Rys. 12.4. Wahadło fizyczne

Moment siły τdziałający na ciało wynosi

(12.13)

co w połączeniu ze wzorem (11.17) daje

(12.14)

Dla małych wychyleń, dla których sinθ ≈ θ dostajemy równanie

(12.15)

Otrzymaliśmy równanie, które ma postać równania (12.3) dla ruchu harmonicznego przy czym θ< odpowiada x. Możemy więc teraz napisać wyrażenie na częstość i okres drgań

(12.16)

(12.17)

Jako przypadek szczególny rozpatrzmy masę punktową zawieszoną na nici o długości l (wahadło proste). Wówczas moment bezwładności I = ml², oraz d = l i otrzymujemy znany wzór dla wahadła prostego

(12.18)

Ćwiczenie
Spróbuj teraz samodzielnie obliczyć okres wahań cienkiej obręczy o masie m i promieniu R zwieszonej na gwoździu G, jak na rysunku obok. Sprawdź obliczenia i wynik.