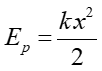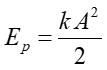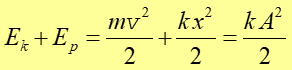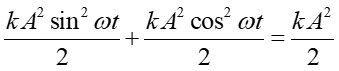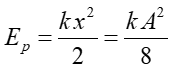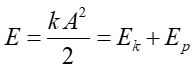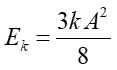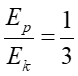12. Ruch drgający
• Spis treści  
• Oscylator harmoniczny tłumiony  
•   Wahadła

12.3 Energia ruchu harmonicznego prostego

  Energię potencjalną sprężyny obliczyliśmy w rozdziale 7.2 przy okazji dyskusji o pracy wykonywanej przez siły zmienne. Pokazaliśmy wtedy, że energia potencjalna sprężyny rozciągniętej o x wynosi

Jeżeli sprężyna zostanie rozciągnięta tak aby masa m znalazła się w chwili t = 0 w położeniu x = A, to energia potencjalna układu

jest zarazem energią całkowitą (energia kinetyczna E_k = 0). Jeżeli puścimy sprężynę to jej energia potencjalna będzie zmieniać się w energię kinetyczną masy m. Przy założeniu, że nie ma tarcia ani innych sił oporu, zgodnie z zasadą zachowania energii suma energii kinetycznej i potencjalnej musi się równać energii całkowitej w dowolnej chwili ruchu

Korzystając z wyrażeń (12.2) i (12.4) na x(t) i v(t) oraz pamiętając, że mω² = k otrzymujemy

Przykład

Spróbujmy teraz obliczyć jaki jest stosunek energii potencjalnej do energii kinetycznej ciała wykonującego drgania harmoniczne, gdy znajduje się ono w połowie drogi między położeniem początkowym, a położeniem równowagi.

Dla danego wychylenia ciała x = A/2 możemy korzystając ze wzoru (12.19) wyliczyć energię potencjalną 

Ponieważ energia całkowita E

więc podstawiając obliczoną wartość energii potencjalnej (12.23) otrzymujemy energię kinetyczną

Widać, że dla x = A/2 energia kinetyczna jest trzykrotnie większa od potencjalnej.