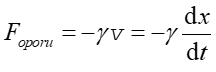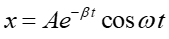12.4 Oscylator harmoniczny tłumiony
Dotychczas pomijaliśmy fakt ewentualnego tłumienia oscylatora to znaczy strat energii układu oscylatora. W przypadku drgań mechanicznych siłą hamującą ruch cząstki są tak zwane opory ruchu. Przykładem może tu być opór powietrza. Więcej o ... Siła oporu ma zwrot przeciwny do prędkości i w najprostszej postaci jest wprost proporcjonalna do prędkości Foporu ~ v
|
(12.27) |
Jeżeli oprócz siły sprężystości uwzględnimy siłę hamującą to równanie opisujące ruch oscylatora harmonicznego przyjmie teraz postać
|
(12.28) |
lub korzystając z równań (3.1)
|
(12.29) |
Jeżeli wprowadzimy nową stałą  (o wymiarze czasu) tak zwaną stałą czasową
(o wymiarze czasu) tak zwaną stałą czasową ![]() oraz oznaczymy częstość drgań nietłumionych czyli częstość
własną
oraz oznaczymy częstość drgań nietłumionych czyli częstość
własną ![]()
 to równanie opisujące ruch przyjmie postać
to równanie opisujące ruch przyjmie postać
|
(12.30) |
Szukamy rozwiązania tego równania w postaci drgań okresowo zmiennych tłumionych na przykład
|
(12.31) |
Proponowane rozwiązanie zawiera czynnik oscylacyjny cosωt opisujący
drgania i czynnik tłumiący  opisujący zmniejszanie się amplitudy drgań. Współczynnik
opisujący zmniejszanie się amplitudy drgań. Współczynnik  określający
wielkość tłumienia nazywamy współczynnikiem
tłumienia
określający
wielkość tłumienia nazywamy współczynnikiem
tłumienia ![]() .
Więcej o ... rozwiązaniu
równania ruchu drgającego tłumionego.
.
Więcej o ... rozwiązaniu
równania ruchu drgającego tłumionego.
Żeby sprawdzić czy zaproponowana funkcja jest rozwiązaniem równania ruchu (12.31) obliczamy odpowiednie pochodne i podstawiamy je do równania ruchu. W wyniku otrzymujemy warunek na częstość drgań tłumionych
|
(12.32) |
Funkcja (12.31) jest rozwiązaniem równania opisującego ruch harmoniczny tłumiony przy warunku (12.32). Widzimy, że opór zmniejsza zarówno amplitudę jak i częstość drgań, czyli powoduje spowolnienie ruchu. Wielkość tłumienia określa współczynnik tłumienia β (lub stała czasowa τ). Wykres ruchu harmonicznego tłumionego w zależności od czasu jest pokazany na rysunku 12.5.

Rys. 12.5. Zależność
przemieszczenia od czasu w ruchu harmonicznym tłumionym.
Linie przerywane ilustrują wykładnicze tłumienie amplitudy tego ruchu
Równanie (12.31)
opisuje sytuację, w której pomimo strat energii zachowany zostaje oscylacyjny charakter ruchu. Ma to miejsce tylko wtedy gdy
spełniony jest warunek β <
ω0
to znaczy dla słabego tłumienia. Tylko wtedy równanie (12.32)
opisuje częstotliwość drgań. Jednak gdy tłumienie (opór) stanie się dostatecznie duże ruch przestaje
być ruchem drgającym, a ciało wychylone z położenia równowagi
powraca do niego asymptotycznie tzw. ruchem pełzającym
![]() (aperiodycznym), a równanie (12.31)
nie jest już rozwiązaniem równania ruchu. Odpowiada to warunkowi
β > ω0
co w praktyce oznacza, że siła tłumiąca jest bardzo duża. Dzieje się tak na przykład gdy
ruch odbywa się w bardzo gęstym ośrodku. Szczególny przypadek odpowiada sytuacji gdy
β = ω0
Mówimy wtedy o tłumieniu krytycznym
(aperiodycznym), a równanie (12.31)
nie jest już rozwiązaniem równania ruchu. Odpowiada to warunkowi
β > ω0
co w praktyce oznacza, że siła tłumiąca jest bardzo duża. Dzieje się tak na przykład gdy
ruch odbywa się w bardzo gęstym ośrodku. Szczególny przypadek odpowiada sytuacji gdy
β = ω0
Mówimy wtedy o tłumieniu krytycznym ![]() .
Wykresy ruchu tłumionego krytycznie i ruchu pełzającego są pokazane na rysunku 12.6 poniżej.
.
Wykresy ruchu tłumionego krytycznie i ruchu pełzającego są pokazane na rysunku 12.6 poniżej.

Rys. 12.6. Ruch pełzający β > ω0 i tłumiony krytycznie β = ω0
|
Symulacje komputerowe Korzystając z załączonego programu możesz prześledzić drgania tłumione wahadła matematycznego w zależności od współczynnika tłumienia β. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera. |
Straty mocy, współczynnik dobroci
Straty energii wynikające z tłumienia opisuje się za pomocą tzw. współczynnika
dobroci Q ![]() ,
który jest definiowany jako
,
który jest definiowany jako
|
Definicja |
|
(12.33) |
gdzie P jest średnią stratą mocy, f częstotliwością drgań. Kilka typowych wartości Q zestawiono w tabeli 12.1.
Tab. 12.1. Współczynnik dobroci Q
| Oscylator | Q |
|---|---|
| Ziemia dla fali sejsmicznej | 250-400 |
| Struna fortepianu lub skrzypiec | 1000 |
| Atom wzbudzony | 107 |
| Jądro wzbudzone | 1012 |


 Energia ruchu harmonicznego prostego
Energia ruchu harmonicznego prostego