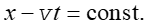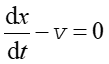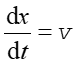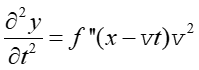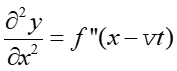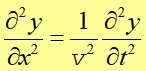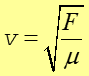Prędkość rozchodzenia się fal, równanie falowe

13.3 Prędkość rozchodzenia się fal, równanie falowe

Jeżeli chcemy zmierzyć prędkość fali v to śledzimy jak przemieszcza się w czasie wybrana część fali czyli określona faza. Dlatego prędkość fali określa się jako prędkość fazową . Dla wybranej fazy fali 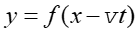poruszającej się w prawo sprowadza się to do warunku

(13.10)

Różniczkując to równanie względem czasu otrzymujemy

(13.11)

czyli

(13.12)

Tak wyraża się prędkość fazowa fali.

W przypadku gdy zaburzenie falowe jest złożeniem fal sinusoidalnych o różnych częstotliwościach to prędkość przenoszenia energii (prędkość fali modulowanej) może być inna niż prędkości fal składowych. Taką prędkość nazywa się prędkością grupową . Więcej o ... prędkości grupowej.

W poprzednim rozdziale pokazaliśmy, że dowolna funkcja f(x - vt) lub f(x + vt) opisuje falę biegnącą odpowiednio w prawo lub lewo wzdłuż osi x i jako przykład rozważaliśmy poprzeczną falę harmoniczną. Teraz poznamy, równanie ruchu falowego, które stosuje się do wszystkich rodzajów fal: zarówno fal mechanicznych takich jak fal dźwiękowych, fal na wodzie, fal w strunach, w sprężynach, jak i do fal elektromagnetycznych takich jak na przykład światło.

Równanie ruchu falowego możemy wyprowadzić wychodząc od ogólnego równania fali 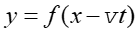. W tym celu obliczamy przyspieszenie poprzecznych drgań punktu ośrodka o współrzędnej x, to znaczy obliczamy drugą pochodną y względem czasu

(13.13)

gdzie v² jest pochodną funkcji wewnętrznej. (Uwaga: w równaniach piszemy pochodne cząstkowe, oznaczane symbolem ∂, bo wychylenie y jest funkcją dwóch zmiennych y = f (x,t))

Równocześnie

(13.14)

Łącząc oba powyższe równania otrzymujemyrównanie różniczkowe ruchu falowego

(13.15)

To równanie spełnia każda funkcja f(x − vt) jak również f(x + vt).

Prędkość v rozchodzenia się fali jest niezależna od amplitudy i częstotliwości, a w przypadku fal mechanicznych zależy od sprężystości ośrodka i jego bezwładności. Na przykład prędkość fali harmonicznej rozchodzącej się wzdłuż naprężonego sznura (struny) jest dana wyrażeniem

(13.16)

gdzie sprężystość sznura jest określona poprzez napinającą go siłę F (im większa siła tym szybciej wychylone elementy sznura wracają do położenia równowagi), a jego bezwładność zależy od masy μ przypadającej na jednostkę długości sznura.

Równanie ruchu falowego można wyprowadzić bezpośrednio z zasad dynamiki Newtona obliczając prędkość fal w naprężonym sznurze. Więcej o ...