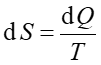16.5 Entropia i druga zasada termodynamiki
Zwróćmy jeszcze raz uwagę na to, że w trakcie pracy (cyklu) silnika
cieplnego część pobieranego ciepła była oddawana do zbiornika o niższej
temperaturze i w konsekwencji ta ilość ciepła nie była zamieniana na
pracę. Powstaje pytanie, czy można skonstruować urządzenie, które
pobierałoby ciepło i w całości zamieniałoby je na pracę? Moglibyśmy
wtedy wykorzystać ogromne (z naszego punktu widzenia nieskończone) ilości
ciepła zgromadzone w oceanach, które byłyby stale uzupełniane poprzez
promieniowanie słoneczne.
Negatywna, niestety, odpowiedź na to pytanie jest zawarta w drugiej
zasadzie termodynamiki. Poniżej podane zostały równoważne sformułowania tej zasady
|
Prawo, zasada, twierdzenie Niemożliwa jest przemiana, której jedynym wynikiem byłaby zamiana na pracę ciepła pobranego ze źródła mającego wszędzie jednakową temperaturę. |
Oznacza to, że nie możemy zbudować doskonałego silnika cieplnego, bo nie możemy wytwarzać pracy pobierając jedynie ciepło z jednego zbiornika bez oddawania pewnej ilości ciepła do zbiornika zimniejszego.
|
Prawo, zasada, twierdzenie Żadna cyklicznie pracująca maszyna nie może bez zmian w otoczeniu przenosić w sposób ciągły ciepła z jednego ciała do drugiego o wyższej temperaturze. |
Wiemy, z doświadczenia, że ciepło przepływa od ciała cieplejszego do ciała zimniejszego. Żeby zmienić ten kierunek musi zostać wykonana praca przez czynnik zewnętrzny. Nie można więc zbudować doskonałej maszyny chłodzącej, która bez dodatkowych efektów (wydatkowania pracy z zewnątrz) przenosiłaby w sposób ciągły ciepło z ciała zimniejszego do cieplejszego.
|
Prawo, zasada, twierdzenie Żadna cykliczna maszyna cieplna pracująca pomiędzy temperaturami T1 i T2 nie może mieć sprawności większej niż (T1−T2)/T1. |
Oznacza to, że żadna maszyna cieplna nie może mieć sprawności większej od sprawności silnika Carnota Więcej o ... .
Przypomnijmy, że sprawność silnika Carnota jest równa
 .
Wynika stąd, że
.
Wynika stąd, że
|
(16.14) |
Możemy więc wyznaczyć stosunek temperatur dowolnych zbiorników ciepła mierząc ilość ciepła przenoszoną podczas jednego cyklu Carnota. Wzór (16.15) stanowi definicję tak zwanej termodynamicznej skali temperatur.
Entropia
Zerowa zasada termodynamiki wiąże się z pojęciem temperatury
![]() .
Pierwsza zasada termodynamiki wiąże się z pojęciem energii
wewnętrznej
.
Pierwsza zasada termodynamiki wiąże się z pojęciem energii
wewnętrznej ![]() .
Natomiast drugą zasadę termodynamiki wiążemy z pojęciem entropii
.
Natomiast drugą zasadę termodynamiki wiążemy z pojęciem entropii
![]() .
.
|
Prawo, zasada, twierdzenie Druga zasada termodynamiki mówi, że w układzie zamkniętym entropia S nie może maleć to znaczy dS ≥ 0. |
Entropia S jest termodynamiczna funkcją stanu, zależy tylko od początkowego i końcowego stanu układu, a nie od drogi przejścia pomiędzy tymi stanami. Entropia jest funkcją określoną dla stanu równowagi, taką że dla procesu odwracalnego
|
Definicja |
|
(16.15) |
lub
|
(16.16) |
gdzie dQ jest ciepłem dostarczanym do układu w procesie odwracalnym.
Z tego punktu widzenia szczególnie interesujące są procesy adiabatyczne nie związane z przepływem ciepła pomiędzy układem i otoczeniem. W procesie adiabatycznym dQ = 0, więc dla procesu odwracalnego dS = 0 na podstawie równania (16.15). Oznacza to, że
|
Prawo, zasada, twierdzenie Entropia układu izolowanego adiabatycznie, w którym zachodzą procesy odwracalne, jest stała. Jednocześnie można pokazać, że dla procesu adiabatycznego nieodwracalnego, entropia układu rośnie. |
Można uogólnić zasadę wzrostu entropii na układy nieizolowane adiabatycznie to znaczy takie, które wymieniają ciepło z otoczeniem. Traktujemy wtedy nasz układ i otoczenie razem jako jeden "większy" układ ponownie izolowany adiabatycznie. Wtedy
|
(16.17) |
gdzie dSo jest zmianą entropii otoczenia. Zmienia się więc entropia naszego układu i otoczenia. Jeżeli proces jest odwracalny to podczas przenoszenia ciepła dQ z otoczenia do naszego układu entropia otoczenia maleje o dQ/T, a entropia układu rośnie o tę samą wartość dQ/T, więc całkowita zmiana entropii jest równa zeru. Zatem posługując się entropią (zgodnie z drugą zasadą termodynamiki) możemy stwierdzić czy dany proces może zachodzić w przyrodzie.
Przykład
Przykładem może być zmiana entropii w gazie doskonałym podczas odwracalnego izotermicznego rozprężania gazu od objętości V1 do objętości V2. Na podstawie pierwszej zasady termodynamiki możemy napisać
|
(16.18) |
a ponieważ dla przemiany izotermicznej dU = 0 więc
|
(16.19) |
Możemy teraz obliczyć entropię na podstawie równania (16.15)
|
(16.20) |
Z równania stanu gazu doskonałego pV = nRT obliczamy T i podstawiając do powyższego wzoru otrzymujemy
|
(16.21) |
|
(16.22) |
Ponieważ gaz się rozpręża to V2 > V1 więc również S2 > S1, czyli entropia rośnie. Aby móc zrealizować ten proces nasz układ musi być w kontakcie ze zbiornikiem o temperaturze T, który dostarcza ciepło i tym samym zapewnia stałą temperaturę rozprężającego się gazu. Entropia tego zbiornika maleje tak, że suma entropii układu i zbiornika nie zmienia się co jest charakterystyczne dla procesu odwracalnego.
Możemy również (posługując się pojęciem entropii) pokazać, że ciepło przepływa z ciała gorącego do zimnego, a nie odwrotnie Więcej o ... .
Entropia a nieuporządkowanie
Entropię układu można opisać na gruncie mechaniki statystycznej.
W takim podejściu entropia jest miarą
nieuporządkowania ![]() układu cząstek. Zgodnie z drugą zasadą termodynamiki dla procesów
zachodzących w przyrodzie entropia układu (wraz z otoczeniem) rośnie to
znaczy, że rośnie również nieuporządkowanie (układu wraz z otoczeniem).
Oznacza to, że im większy jest stan nieporządku (położeń i prędkości
cząstek) w układzie tym większe jest prawdopodobieństwo, że układ będzie
w tym stanie.
układu cząstek. Zgodnie z drugą zasadą termodynamiki dla procesów
zachodzących w przyrodzie entropia układu (wraz z otoczeniem) rośnie to
znaczy, że rośnie również nieuporządkowanie (układu wraz z otoczeniem).
Oznacza to, że im większy jest stan nieporządku (położeń i prędkości
cząstek) w układzie tym większe jest prawdopodobieństwo, że układ będzie
w tym stanie.
Z definicji, entropia układu jest równa
|
Definicja |
|
(16.23) |
gdzie, k jest stałą Boltzmana, a ω liczbą stanów mikroskopowych realizujących stan makroskopowy, którego entropię liczymy.
Pokażmy teraz, że to sformułowanie jest równoważne definicji termodynamicznej entropii. W tym
celu rozpatrzmy swobodne rozprężanie gazu od objętości V1
do objętości końcowej V2.
Względne prawdopodobieństwo znalezienia jednej cząstki w objętości V1
w porównaniu do V2 jest równe
|
(16.24) |
|
(16.25) |
Obliczamy teraz zmianę entropii układu
|
(16.26) |
Podstawiając zależność (16.26) otrzymujemy
|
(16.27) |
Równanie to można przekształcić, dzieląc je i mnożąc przez T, do postaci
|
(16.28) |
gdzie wyrażenie w liczniku jest równe ilości ciepła dostarczonego do układu, aby ten przeszedł do stanu końcowego w sposób odwracalny rozprężając się izotermiczne (rozdział 15.6).
Ostatecznie więc
|
(16.29) |
gdzie dQ jest ciepłem dostarczanym do układu w procesie odwracalnym.
Podsumowując, w ujęciu termodynamicznym stan równowagi odpowiada stanowi o największej entropii, a w ujęciu statystycznym jest stanem najbardziej prawdopodobnym.


 Procesy odwracalne i nieodwracalne, cykl Carnota
Procesy odwracalne i nieodwracalne, cykl Carnota
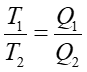

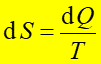
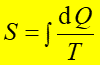
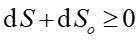
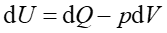
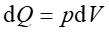
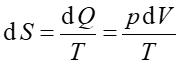
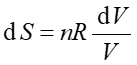
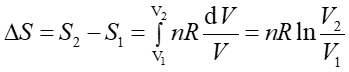
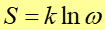
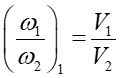
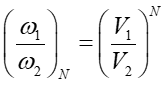
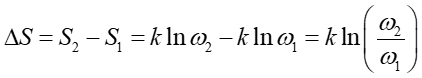

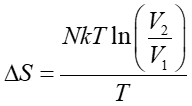
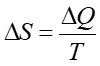 lub
lub