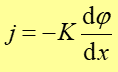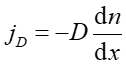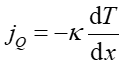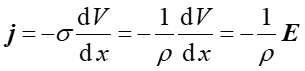16. Kinetyczna teoria gazów i termodynamika II
• Spis treści  
• Podsumowanie  
•   Entropia i druga zasada termodynamiki

16.6 Stany równowagi, zjawiska transportu

Stany równowagi

  W dotychczasowych naszych rozważaniach posługiwaliśmy się pojęciem stanu równowagi układu , czyli stanu, w którym żaden z parametrów potrzebnych do makroskopowego opisu układu nie zależy od czasu. Zajmowaliśmy się procesami, które zaczynały się jednym stanem równowagi, a kończyły innym stanem równowagi.
Dla układu jednorodnego (przykładowo gazu) w stanie równowagi do jego opisu wystarcza znajomość dwu podstawowych parametrów stanu na przykład ciśnienia i objętości. Opis komplikuje się gdy mamy układ niejednorodny na przykład ciecz w równowadze z parą. Dla danej temperatury stan równowagi tego układu jest możliwy przy różnych objętościach układu (od objętości zależy ilość fazy ciekłej i gazowej). Natomiast temperatura i ciśnienie przestają być niezależne. W każdej temperaturze równowaga jest możliwa tylko przy określonym ciśnieniu (pary nasyconej). Przy wyższym istnieje tylko ciecz, przy niższym para. Podobnie ciecz i ciało stałe mogą istnieć w równowadze tylko w temperaturze topnienia, która jest funkcją ciśnienia. Wreszcie ciało stałe współistnieje w równowadze z parą nasyconą, której ciśnienie jest funkcją temperatury. Krzywe równowagi pokazane na rysunku 16.6.

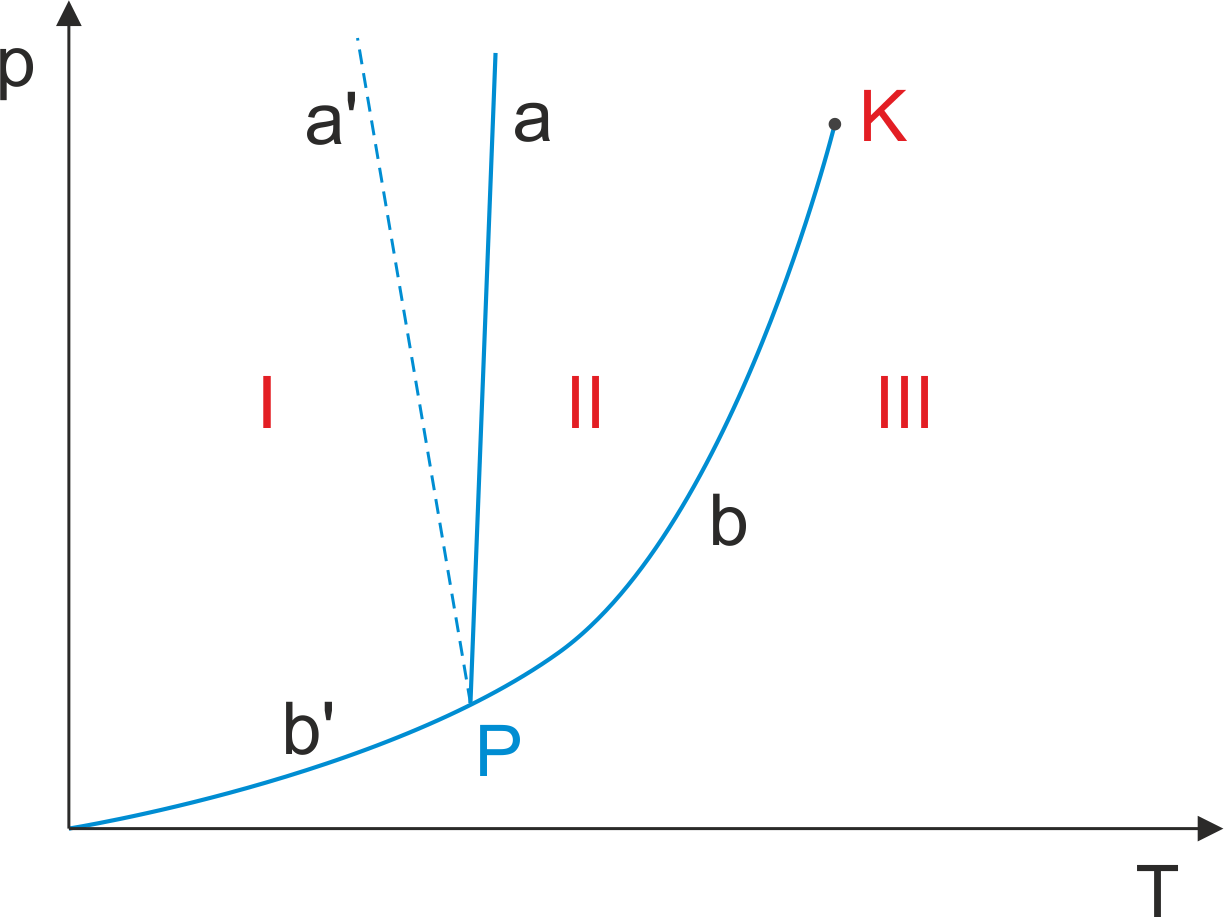
 Rys. 16.6. Krzywe równowagi dla układu niejednorodnego.
Obszar I - ciało stałe, obszar II - ciecz, obszar III - gaz

Literą a oznaczona jest krzywa równowagi ciało stałe - ciecz (związek temperatury topnienia z ciśnieniem). Krzywa a' przedstawia tę zależność dla kilku nietypowych substancji, które przy topnieniu zmniejszają objętość na przykład dla lodu. Krzywa b + b' pokazuje zależność ciśnienia pary nasyconej od temperatury. Odcinek b' to krzywa równowagi ciało stałe - para, a odcinek b to krzywa równowagi ciecz - para. Krzywa równowagi ciecz - para kończy się w punkcie krytycznym K. Dla temperatury wyższej od temperatury punktu krytycznego K zanika różnica pomiędzy fazą ciekłą i gazową. Dlatego warunkiem skroplenia gazu jest ochłodzenie go poniżej jego temperatury krytycznej.
Punkt P, w którym łączą się krzywe nazywamy punktem potrójnym. W tym punkcie mogą znajdować się w równowadze wszystkie trzy stany skupienia. Dla wody odpowiada to ciśnieniu p = 610.6 Pa i T = 273.16 K (0.01 °C). Punkt potrójny wody posłużył do definicji jednostki temperatury - kelwina.

Zjawiska transportu

Znajomość dochodzenie układów do stanów równowagi jest równie ważna jak znajomość ich własności w stanach równowagi, a każdy układ pozostawiony samemu sobie przez dostatecznie długi czas dochodzi do stanu równowagi.

Teraz zapoznamy się z bardzo uproszczonym opisem zjawisk, które zachodzą gdy układy dążą do stanów równowagi. W zjawiskach tych mamy zawsze do czynienia z przenoszeniem (transportem) materii, energii, pędu lub ładunku elektrycznego. Wszystkie te zjawiska transportu opisujemy w pierwszym przybliżeniu za pomocą takiego samego równania różniczkowego, które przedstawia propagację (rozprzestrzenianie się) pewnej wielkości fizycznej φ mającą na celu osiągnięcie równowagi

W tym równaniu j jest gęstością strumienia (gęstość prądu) wielkości fizycznej φ, a K jest stałą charakteryzującą daną sytuację fizyczną. Stałą K wiążemy z właściwościami mikroskopowymi rozpatrywanego układu statystycznego. Jest to tak zwany współczynnik transportu .

Omówimy teraz krótko wybrane zjawiska transportu:

Dyfuzja w gazie czyli przenoszenie cząstek w kierunku obszarów o mniejszej koncentracji n (dążenie do wyrównania koncentracji). Równanie (16.30) nosi teraz nazwę równania dyfuzji i ma postać

gdzie j_D jest gęstością strumienia cząstek, dn/dx jest różnicą stężeń występującą na odległości dx, a D współczynnikiem dyfuzji. Równanie to znane jest pod nazwą prawa Ficka. Ponieważ dyfuzja jest przenoszeniem cząstek (z miejsc o większym stężeniu do miejsc o mniejszym stężeniu) więc mamy do czynienia z transportem masy.

Przewodnictwo cieplne czyli transport energii wskutek ruchu cząstek w kierunku obszaru o niższej T (dążenie do wyrównania temperatury). Równanie transportu ciepła ma postać

gdzie j_Q jest gęstością strumienia ciepła, dT/dx jest różnicą temperatur w warstwie ciała o grubości dx, a κ jest współczynnikiem przewodnictwa cieplnego. Równanie to znane jest pod nazwą prawa Fouriera.

Przewodnictwo elektryczne czyli przenoszenie ładunku elektrycznego w wyniku ruchu elektronów (dążenie do wyrównania potencjałów elektrycznych). Równanie, zwane prawem Ohma, ma postać

gdzie dV/dx jest różnicą potencjałów (napięciem) pomiędzy punktami przewodnika odległymi o dx, σ przewodnością elektryczną, ρ opornością właściwą, a E natężeniem pola elektrycznego.

Uwaga: wszystkie współczynniki transportu zależą od temperatury.

Ten rozdział kończy moduł czwarty; możesz teraz przejść do podsumowania i zadań testowych.