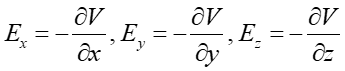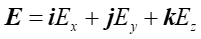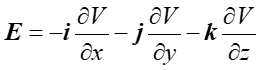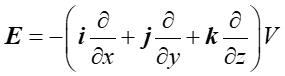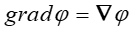Potencjał elektrycznyGradient pola
Przy pomocy obliczania pochodnych cząstkowych ze skalarnego potencjału V otrzymaliśmy składowe wektora pola E w dowolnym punkcie przestrzeni
|
(1) |
|
(2) |
|
(3) |
To równanie można zapisać w postaci
|
(4) |
gdzie wyrażenie w nawiasie jest operatorem wektorowym
nabla 
,
który oznaczamy symbolem ∇.
Nazywamy tę wielkość operatorem ponieważ nie ma ona konkretnego
znaczenia dopóki nie działa (operuje) na jakąś funkcję taką jak na
przykład potencjał V.
Operator ten ma istotne znaczenie gdy mamy do czynienia z polami skalarnymi i wektorowymi. Pole skalarne to
takie pole, która ma przypisaną wartość skalarną (liczbową) w każdym
punkcie przestrzeni. Natomiast pole wektorowe ma w każdym punkcie przestrzeni przypisany wektor.
Dla dowolnego pola skalarnego φ(x,y,z)
można działając na nie operatorem ∇ utworzyć pole wektorowe, które nazywamy
gradientem φ
.
|
(5) |
Gradient potencjału, gradφ ma wartość równą maksymalnej zmianie potencjału φ (maksymalne nachylenie funkcji φ(x,y,z)) i zwrot (gradφ jest wektorem) przeciwny do kierunku, w którym zmiana φ jest największa.