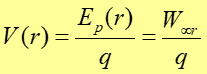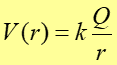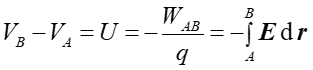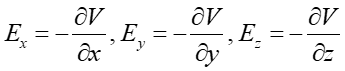Potencjał elektryczny

19.2 Potencjał elektryczny

Jak pokazaliśmy w poprzednim paragrafie energia potencjalna ładunku w polu elektrycznym zależy od wielkości tego ładunku. Dlatego do opisu pola elektrycznego lepiej posługiwać się energią potencjalną przypadającą na jednostkowy ładunek czyli potencjałem elektrycznym.

Definicja
Potencjał elektryczny definiujemy jako energię potencjalną pola elektrycznego podzieloną przez jednostkowy ładunek.

(19.5)

Jednostki
W układzie SI jednostką potencjału elektrycznego jest wolt (V); 1V = 1J/C.

Potencjał pola ładunku punktowego Q możemy otrzymać natychmiast dzieląc równanie (19.4) obustronnie przez q

(19.6)

Obliczony potencjał określa pracę potrzebną do przeniesienia jednostkowego ładunku z nieskończoności na odległość r od ładunku Q. Potencjał charakteryzuje pole elektryczne; a nie zależy od umieszczonego w nim ładunku.

Ćwiczenie
Spróbuj obliczyć potencjał na powierzchni jądra miedzi. Promień jądra wynosi równy 4.8·10⁻¹⁵ m. Przyjmij, że rozkład 29 protonów w jądrze miedzi jest kulisto-symetryczny. W związku z tym potencjał na zewnątrz jądra jest taki jakby cały ładunek skupiony był w środku i możesz posłużyć się wzorem (19.6). Ponadto oblicz potencjalną energię elektryczną elektronu poruszającego się po pierwszej orbicie w polu elektrycznym jądra miedzi. Przyjmij promień orbity równy 5·10⁻¹¹ m. Sprawdź obliczenia i wynik.

Często w fizyce posługujemy się pojęciem różnicy potencjałów czyli napięciem (oznaczanym U ). Różnica potencjałów między dwoma punktami A i B jest równa pracy potrzebnej do przeniesienia w polu elektrycznym ładunku jednostkowego (próbnego) q pomiędzy tymi punktami. Wyrażenie na różnicę potencjałów otrzymamy bezpośrednio ze wzoru (19.2) dzieląc to równanie obustronnie przez q otrzymujemy

(19.7)

Znak minus odzwierciedla fakt, że potencjał maleje w kierunku wektora E.

Podobnie jak natężenie pola elektrycznego, które ilustrowaliśmy za pomocą linii sił pola (paragraf 17.3) również potencjał elektryczny można przedstawialiśmy graficznie. W tym celu rysujemy powierzchnie lub linie ekwipotencjalne , które przedstawiają w przestrzeni zbiory punktów o jednakowym potencjale.

Jako przykład pokazany jest na rysunku 19.1 poniżej rozkład potencjału, na płaszczyźnie xy, wokół ładunku punktowego i dipola elektrycznego. Kolorem czerwonym zaznaczono wybrane linie łączą punkty o jednakowym potencjale - linie ekwipotencjalne (każda krzywa odpowiada innej stałej wartości potencjału).

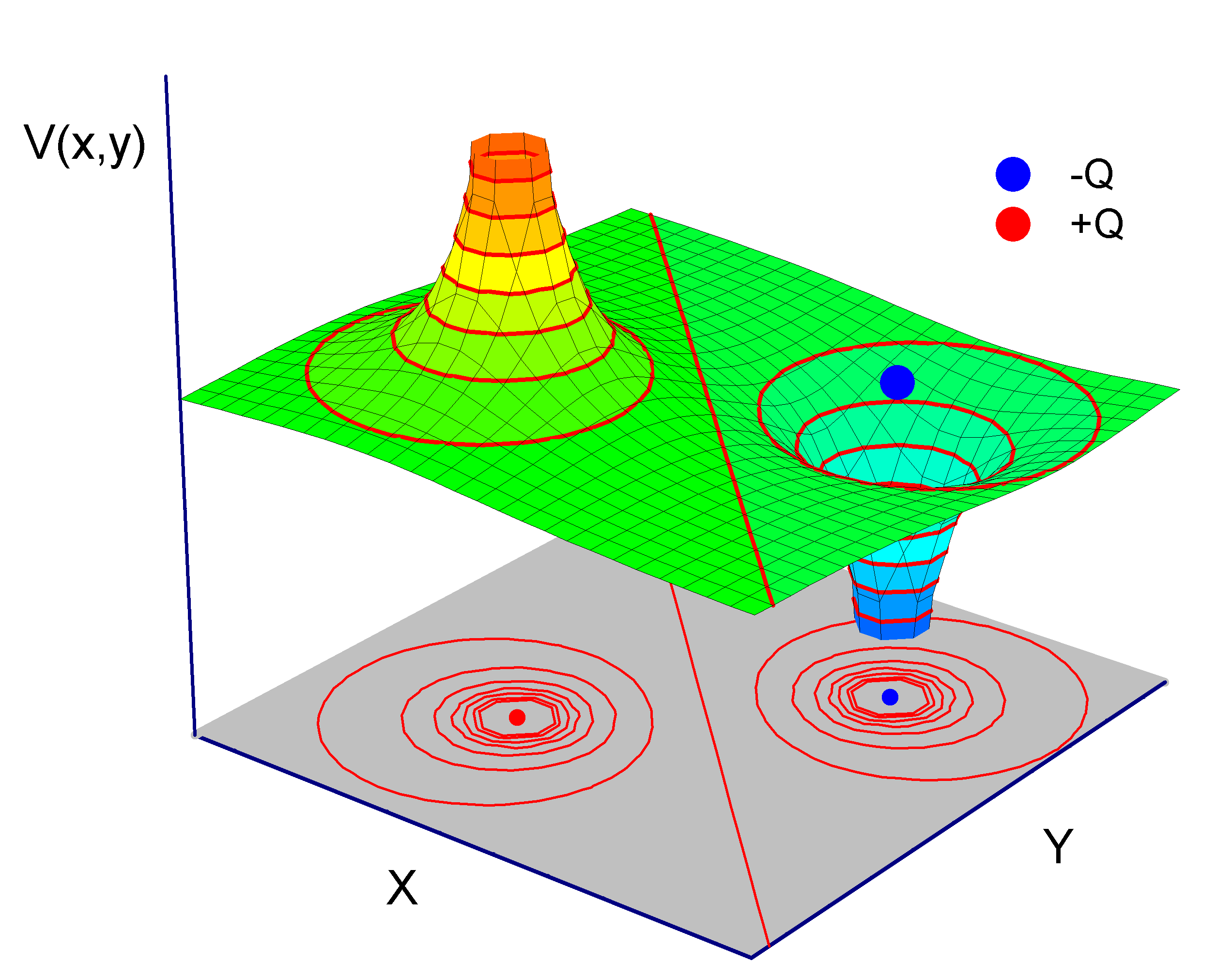
Rys. 19.1. Potencjał elektryczny dipola elektrycznego (na płaszczyźnie xy)

Gdy znamy rozkład potencjału elektrycznego wytworzonego w każdym punkcie przestrzeni przez dany układ ładunków to na podstawie wielkości zmiany potencjału, przypadającej na jednostkę długości, w danym kierunku, możemy określić natężenie pola elektrycznego E w tym kierunku. Warunek ten (we współrzędnych x, y, z) wyraża się następująco

(19.8)

Możemy więc przy pomocy obliczania pochodnych cząstkowych z wielkości skalarnej (potencjału V) otrzymać składowe wielkości wektorowej (pola E) w dowolnym punkcie przestrzeni Więcej o ... .

Im większa (mniejsza) zmiana potencjału na jednostkę długości tym większe (mniejsze) pole elektryczne w danym kierunku. Znak minus odzwierciedla fakt, że wektor E jest skierowany w stronę malejącego potencjału. Kierunek pola elektrycznego w dowolnym punkcie odpowiada kierunkowi wzdłuż którego potencjał spada najszybciej co oznacza, że linie sił pola są prostopadłe do powierzchni (linii) ekwipotencjalnych. Zostało to zilustrowane na rysunku poniżej gdzie pokazane są powierzchnie ekwipotencjalne (linie ich przecięcia z płaszczyzną rysunku) oraz linie sił pola (a) ładunku punktowego, (b) dipola elektrycznego (porównaj z rysunkiem 19.1).

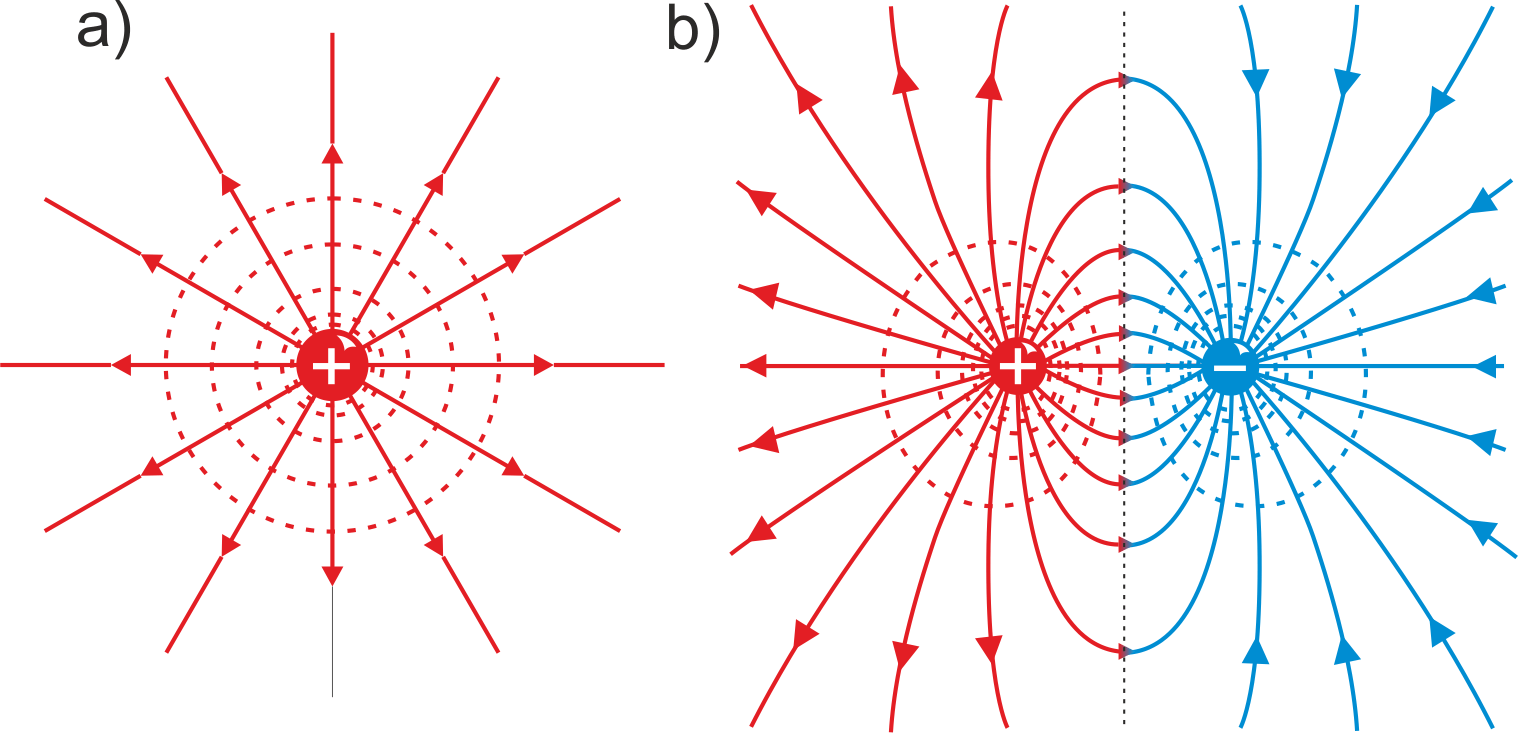
Rys. 19.2. Powierzchnie ekwipotencjalne (linie czerwone) i linie sił pola (linie niebieskie): (a) ładunku punktowego,
(b) dipola elektrycznego; linie ekwipotencjalne oznaczają przecięcia powierzchni ekwipotencjalnych z płaszczyzną rysunku

Wzory wyrażające związek pomiędzy potencjałem i polem elektrycznym są bardzo użyteczne bo na ogół łatwiej obliczyć i zmierzyć potencjał niż natężenie pola.

Symulacje komputerowe
Korzystając z załączonego programu możesz prześledzić rozkład linii (powierzchni) ekwipotencjalnych dla różnych układów ładunków. Przed uruchomieniem zobacz krótki opis programu . Program można pobrać i zapisać go na dysku twardym własnego komputera.

W paragrafie 18.3. pokazaliśmy, że cały ładunek umieszczony na izolowanym przewodniku gromadzi się na jego powierzchni i że pole E musi być prostopadłe do powierzchni bo gdyby istniała składowa styczna do powierzchni to elektrony przemieszczałyby się. W oparciu o wyrażenie (19.7) możemy podać alternatywne sformułowanie. Jeżeli pole E wzdłuż powierzchni przewodnika równa się zeru to różnica potencjałów też równa się zeru ΔV = 0. Oznacza to, że

Prawo, zasada, twierdzenie
Powierzchnia każdego przewodnika w stanie ustalonym jest powierzchnią stałego potencjału (powierzchnią ekwipotencjalną).

Teraz przejdziemy do obliczeń potencjału elektrycznego dla różnych naładowanych ciał.