Obliczanie potencjału elektrycznego

19.3 Obliczanie potencjału elektrycznego

Jako przykład rozważymy różnicę potencjałów między powierzchnią i środkiem sfery o promieniu R naładowanej jednorodnie ładunkiem Q. Jak pokazaliśmy w punkcie 18.3 pole elektryczne wewnątrz naładowanej sfery (r < R) jest równe zeru E = 0. Oznacza to (równanie 19.7), że różnica potencjałów też jest równa zeru V_B − V_A = 0, tzn. potencjał w środku jest taki sam jak na powierzchni sfery. Natomiast na zewnątrz (dla r ≥ R) potencjał jest taki jak dla ładunku punktowego skupionego w środku sfery, czyli jest dany równaniem (19.6).
Zależność potencjału i odpowiadającego mu natężenia pola od odległości od środka naładowanej sfery jest pokazana na rysunku 19.3.

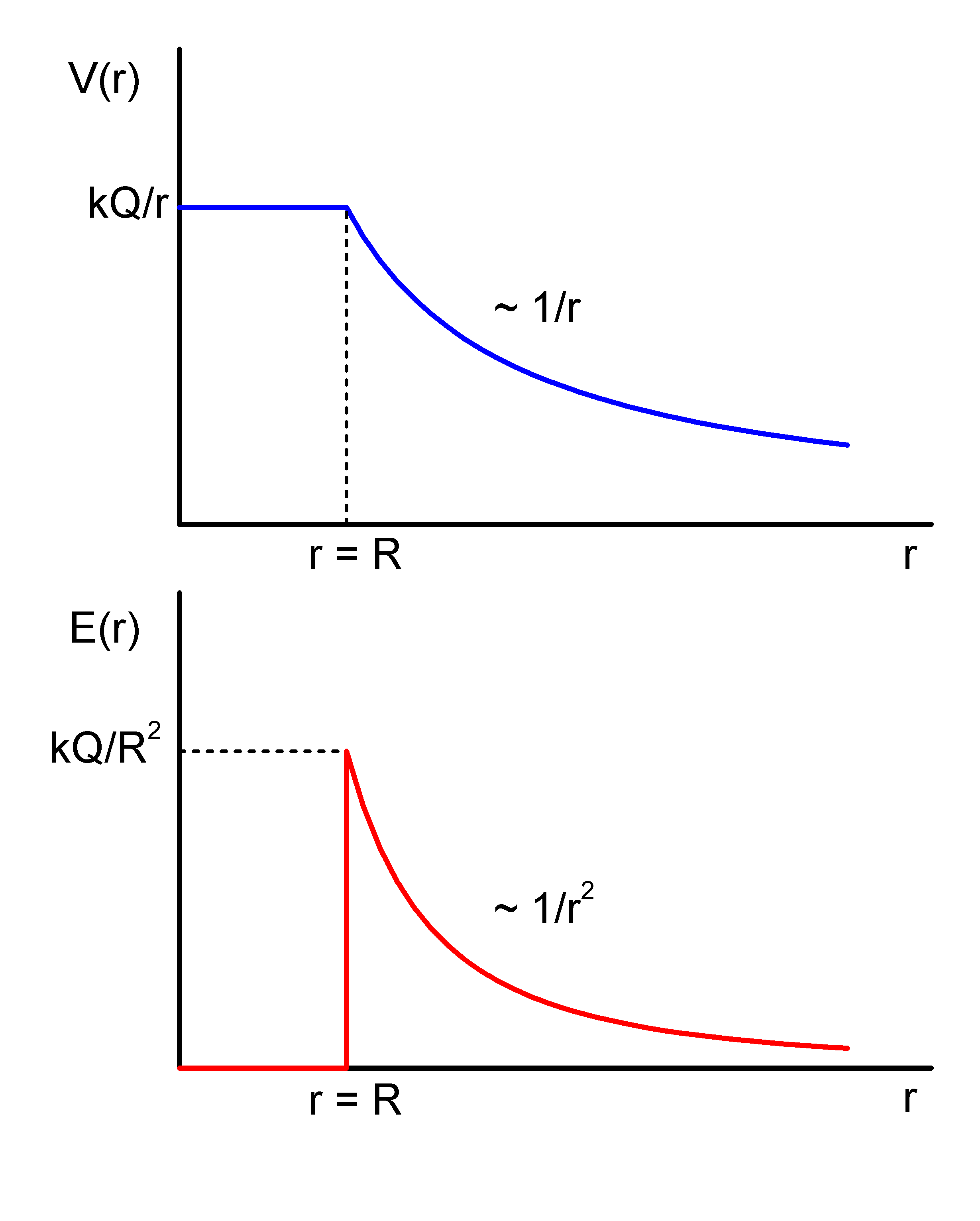
Rys. 19.3. Porównanie zależności potencjału i natężenia pola elektrycznego od odległości od środka naładowanej sfery

Porównując dwa powyższe wykresy V(r) i E(r) możemy zauważyć, że istnieje miedzy nimi związek dany wyrażeniem

(19.9)

W każdym punkcie natężenie pola E(r) jest równe nachyleniu wykresu V(r) ze znakiem minus.

Ten związek pomiędzy natężeniem pola i potencjałem wynika wprost z równania (19.7) bo na jego mocy dV = E dr.

Obliczanie potencjału dla układu ładunków punktowych prześledzimy na przykładzie potencjału dipola. W tym celu rozpatrzymy punkt P odległy o r od środka dipola tak jak to widać na rys. 19.4. Położenie punktu P jest określone poprzez r i θ.

Rys. 19.4. Dipol elektryczny

Korzystamy z zasady superpozycji:

Prawo, zasada, twierdzenie
Całkowity potencjał pola pochodzącego od układu ładunków punktowych w dowolnym punkcie obliczamy sumując potencjały od poszczególnych ładunków.

Dlatego potencjał w punkcie P pochodzący od ładunków Q i −Q wynosi

(19.10)

To jest ścisłe wyrażenie na potencjał dipola ale do jego obliczenia potrzeba znać r₁ oraz r₂. My natomiast rozważymy tylko punkty odległe od dipola, dla których r >> l. Dla takich punktów możemy przyjąć z dobrym przybliżeniem, że oraz . Po uwzględnieniu tych zależności wyrażenie na potencjał przyjmuje postać

(19.11)

gdzie p = Ql jest momentem dipolowym.

Ćwiczenie
Wykonaj ścisłe obliczenia potencjału elektrycznego tego dipola w punkcie leżącym odpowiednio: a) na symetralnej dipola tj. na osi y w odległości r od jego środka, b) na dodatniej półosi x w odległości r od środka dipola, c) na ujemnej półosi x w odległości r od środka dipola. Sprawdź obliczenia i wynik.

Teraz wrócimy do przykładu z paragrafu 18.4 i obliczymy różnicę potencjałów dla dwóch przeciwnie naładowanych płyt o polu powierzchni S każda, znajdujących się w odległości d od siebie. Ładunki na płytach wynoszą odpowiednio +Q i −Q więc gęstość powierzchniowa ładunku σ = Q/S. Ze wzoru (19.7) wynika, że

(19.12)

a ponieważ, zgodnie z naszymi obliczeniami, pole pomiędzy płytami jest równe E = σ/ε₀ więc

(19.13)

lub

(19.14)