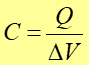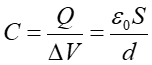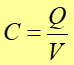Obliczanie potencjału elektrycznego20.1 Pojemność elektryczna
Układ dwóch przewodników, który może
gromadzić ładunek elektryczny, przy przyłożonej różnicy potencjałów,
nazywamy kondensatorem 
,
a te przewodniki okładkami kondensatora. Rysunek 20.1 przedstawia
kondensator płaski, w którym przewodniki (okładki) stanowią dwie równoległe
płytki przewodzące.
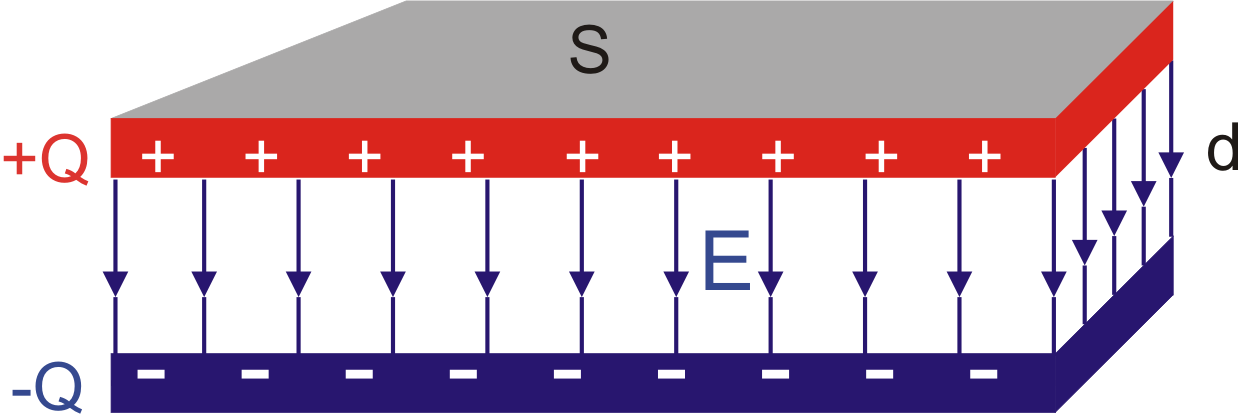
Rys. 20.1. Kondensator płaski
Wielkością charakteryzującą kondensator jest jego pojemność, która definiujemy następująco
|
Definicja Pojemnością elektryczną nazywamy stosunek ładunku kondensatora do różnicy potencjałów (napięcia) między okładkami. |
|
(20.1) |
Zwróćmy uwagę, że Q jest ładunkiem na każdym przewodniku, a nie ładunkiem wypadkowym na kondensatorze (ładunek wypadkowy równy jest zeru).
Pojemność kondensatora płaskiego możemy obliczyć z definicji (20.1) korzystając z równania (19.14)
|
(20.2) |
Zauważmy, że pojemność zależy od kształtu okładek, ich rozmiaru i wzajemnego położenia. Oznacza to, że dla kondensatorów o innej geometrii obowiązują inne wzory. Równanie (20.2) obowiązuje dla kondensatora płaskiego znajdującego się w próżni. Zależność pojemność kondensatora od przenikalności elektrycznej ośrodka omówimy później.
|
Jednostki W układzie SI jednostką pojemności jest farad (F); 1F = 1C/1V. Powszechnie stosuje się jednak mniejsze jednostki: μF, nF, pF. |
|
Ćwiczenie Żeby przekonać się, że farad jest dużą jednostką oblicz pojemność próżniowego kondensatora płaskiego, którego okładki o powierzchni 1 cm2 są umieszczone w odległości 1 mm od siebie. Sprawdź obliczenia i wynik. |
Kondensatory są częścią składową prawie wszystkich układówelektronicznych. W celu dobrania odpowiedniej pojemności powszechnie stosuje się ich łączenie w układy szeregowe lub równoległe.
|
Ćwiczenie Spróbuj samodzielnie wyprowadzić (lub podać) wzory na pojemność wypadkową układu kondensatorów połączonych szeregowo i równolegle. Pamiętaj, że kondensatory połączone szeregowo mają jednakowy ładunek, a połączone równolegle jednakową różnicę potencjałów. Sprawdź obliczenia i wynik. |
|
Definicja Pojemnością elektryczną przewodnika nazywamy stosunek ładunku umieszczonego na przewodniku do potencjału jaki ma ten przewodnik w polu elektrycznym wytworzonym przez ten ładunek. |
|
(20.3) |
Można więc dany przewodnik uważać za jedną z okładek kondensatora, w którym druga okładka kondensatora znajduje się w nieskończoności i ma potencjał równy zeru.