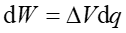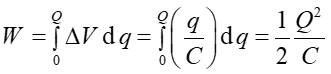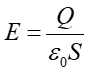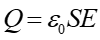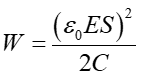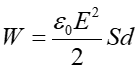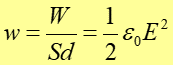Pojemność elektryczna20.2 Energia pola elektrycznego
Rozpatrzmy początkowo nienaładowany kondensator, który ładujemy przenosząc elektrony pomiędzy okładkami. Okładka, z której zabieramy elektrony ładuje się dodatnio, a okładka na którą je przenosimy ujemnie. W wyniku tego postępowania różnica potencjałów rośnie od 0 do ΔV, a ładunek na kondensatorze wzrasta od 0 do Q.
Praca zużyta na przeniesienie porcji ładunku dq pomiędzy okładkami przy panującej w danej chwili różnicy potencjałów ΔV wynosi zgodnie ze wzorem (19.7)
|
(20.4) |
Musimy przy tym pamiętać, że w trakcie ładowania kondensatora różnica potencjałów rośnie więc przenoszenie dalszych porcji ładunku jest coraz trudniejsze (wymaga więcej energii). Całkowita praca na przeniesienie ładunku Q, równa energii potencjalnej zgromadzona w kondensatorze, wynosi zatem
|
(20.5) |
gdzie skorzystaliśmy ze wzoru (20.1) na pojemność.
Przypomnijmy, że dla kondensatora płaskiego (paragraf 18.4)
|
(20.6) |
|
(20.7) |
Po podstawieniu do wzoru (20.5) otrzymujemy
|
(20.8) |
Uwzględniając ponadto wyrażenie (20.2) na pojemność kondensatora płaskiego ostatecznie
|
(20.9) |
Zauważmy, że iloczyn Sd jest objętością kondensatora, więc gęstość energii w (pola elektrycznego), która jest energią zawartą w jednostce objętości wynosi
|
(20.10) |
|
Prawo, zasada, twierdzenie Jeżeli w jakimś punkcie przestrzeni istnieje pole elektryczne o natężeniu E to możemy uważać, że w tym punkcie jest zmagazynowana energia w ilości ½ε0E2 na jednostkę objętości. |
