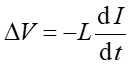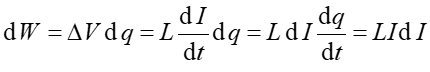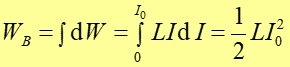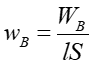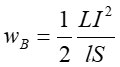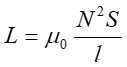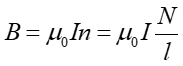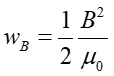24. Indukcja elektromagnetyczna
• Spis treści  
• Drgania w obwodzie LC  
•   Indukcyjność

24.4 Energia pola magnetycznego

  W paragrafie 20.2 pokazaliśmy, że jeżeli w jakimś punkcie przestrzeni istnieje pole elektryczne o natężeniu E to możemy uważać, że w tym punkcie jest zmagazynowana energia w ilości ε₀E²/2 na jednostkę objętości. Podobnie energia może być zgromadzona w polu magnetycznym. Rozważmy na przykład obwód zawierający cewkę o indukcyjności L. Jeżeli do obwodu włączymy źródło SEM (np. baterię) to prąd w obwodzie narasta od zera do wartości maksymalnej I₀. Zmiana prądu w obwodzie powoduje powstanie na końcach cewki różnicy potencjałów ΔV (SEM indukcji) przeciwnej do SEM przyłożonej

Do pokonania tej różnicy potencjałów przez ładunek dq potrzeba jest energia (praca) dW

Energię tę (pobraną ze źródła SEM) ładunek przekazuje cewce więc energia cewki wzrasta o dW. Całkowita energia magnetyczna zgromadzona w cewce podczas narastania prądu od zera do I₀ wynosi więc<

Jeżeli rozpatrywana cewka ma długości l i powierzchnię przekroju S, to jej objętość jest równa iloczynowi lS i gęstość energii magnetycznej zgromadzonej w cewce wynosi

lub na podstawie równania (24.22)

Przypomnijmy, że dla cewki indukcyjność i pole magnetyczne dane są odpowiednio przez wyrażenia

co prowadzi do wyrażenie opisującego gęstość energii magnetycznej w postaci

Prawo, zasada, twierdzenie Jeżeli w jakimś punkcie przestrzeni istnieje pole magnetyczne o indukcji B to możemy uważać, że w tym punkcie jest zmagazynowana energia w ilości 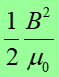na jednostkę objętości.