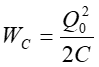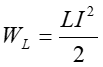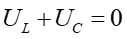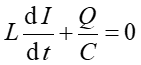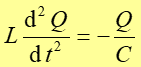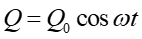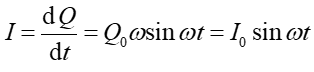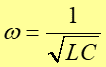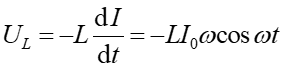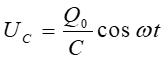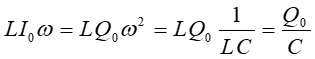25. Drgania elektromagnetyczne
• Spis treści  
• Obwód szeregowy RLC  
•   Energia pola magnetycznego

25.1 Drgania w obwodzie LC

  Rozpatrzmy obwód złożony z szeregowo połączonych indukcyjności L (cewki) i pojemności C (kondensatora) pokazany na rysunku 25.1. Przyjmijmy, że opór elektryczny (omowy) obwodu jest równy zeru (R = 0). Załóżmy też, że w chwili początkowej na kondensatorze C jest nagromadzony ładunek Q₀, a prąd w obwodzie nie płynie (rysunek a). W takiej sytuacji energia zawarta w kondensatorze

co prowadzi do wyrażenie opisującego gęstość energii magnetycznej w postaci

jest maksymalna, a energia w cewce

jest równa zeru.

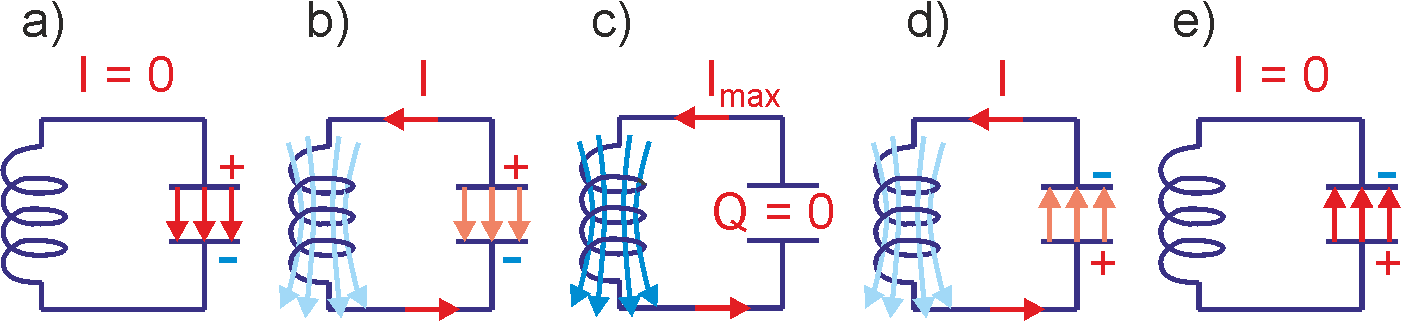
 Rys. 25.1. Oscylacje w obwodzie LC

Następnie kondensator zaczyna rozładowywać się (rysunek b). W obwodzie płynie prąd I = dQ/dt. W miarę jak maleje ładunek na kondensatorze maleje też energia zawarta w polu elektrycznym kondensatora, a rośnie energia pola magnetycznego, które pojawia się w cewce w miarę narastania w niej prądu.

Wreszcie gdy ładunek spadnie do zera cała energia jest przekazana do pola magnetycznego cewki (rysunek c). Jednak pomimo, że kondensator jest całkowicie rozładowany prąd dalej płynie w obwodzie (w tym samym kierunku). Jego źródłem jest SEM  samoindukcji powstająca w cewce, która podtrzymuje słabnący prąd.

Ten prąd ładuje kondensator (przeciwnie) więc energia jest ponownie przekazywana do kondensatora (rysunek d).

Wreszcie ładunek na kondensatorze osiąga maksimum, a prąd w obwodzie zanika. Stan końcowy jest więc taki jak początkowy tylko kondensator jest naładowany odwrotnie (rysunek e).

Sytuacja powtarza się, tylko teraz prąd rozładowania kondensatora będzie płynął w przeciwnym kierunku. Mamy więc do czynienia z oscylacjami (drganiami) ładunku (prądu). Zmienia się zarówno wartość jak i znak (kierunek) ładunku na kondensatorze i prądu w obwodzie.

Do opisu ilościowego tych drgań skorzystamy z prawa Kirchhoffa, zgodnie z którym

gdzie U_L i U_C są napięciami odpowiednio na cewce i kondensatorze. Korzystając z równań (24.16) i (20.1) otrzymujemy

Ponieważ I = dQ/dt więc

Jest to równanie drgań w obwodzie LC.

Równanie to opisujące oscylacje ładunku ma identyczną postać jak równanie (12.3) drgań swobodnych masy zawieszonej na sprężynie, przy czym następujące wielkości elektryczne odpowiadają wielkościom mechanicznym: ładunek Q  → przesunięcie x; indukcyjność L → masa m; pojemność C → odwrotność współczynnika sprężystości 1/k; prąd I = dQ/dt → prędkość v = dx/dt.

Ponieważ zagadnienie drgań swobodnych zostało rozwiązane w paragrafie 12.1 więc możemy skorzystać z uprzednio wyprowadzonych wzorów i napisać rozwiązanie równania (25.5)

gdzie częstość drgań jest dana wyrażeniem

Możemy teraz obliczyć napięcie chwilowe na cewce i kondensatorze

Zauważmy, że maksymalne wartości (amplitudy) tych napięć są takie same

Z powyższych wzorów wynika, że w obwodzie LC ładunek na kondensatorze, natężenie prądu i napięcie zmieniają się sinusoidalnie tak jak dla drgań harmonicznych. Zauważmy ponadto, że między napięciem i natężeniem prądu istnieje różnica faz, równa π/2. Gdy napięcie osiąga maksymalną wartość to prąd jest równy zeru i na odwrót.

Podsumowując: w obwodzie LC  obserwujemy oscylacje (drgania) pola elektrycznego w kondensatorze i pola magnetycznego w cewce. Mówimy, że w obwodzie LC obserwujemy drgania elektromagnetyczne , a sam obwód LC nazywamy obwodem drgającym .

Ćwiczenie Korzystając ze wzorów (25.1) i (25.2)  oraz z podanego rozwiązania równania drgań oblicz energię jaka jest zgromadzona w dowolnej chwili t w kondensatorze i w cewce indukcyjnej. Ile wynosi energia całkowita? Pamiętaj, że . Sprawdź obliczenia i wynik.

 Więcej o ...  innych obwodach (RC, RL), w których natężenie prądu zmienia się w czasie.