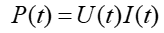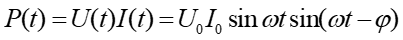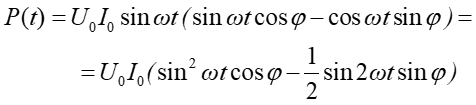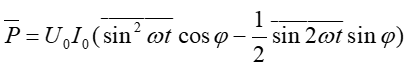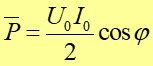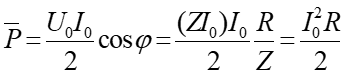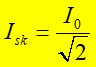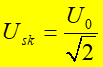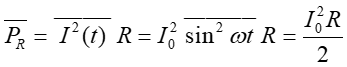Rezonans25.4 Moc w obwodzie prądu zmiennego
O mocy wydzielanej w obwodzie prądu stałego mówiliśmy w rozdziale 21. W obwodzie prądu zmiennego moc dana jest takim samym wyrażeniem
|
(25.25) |
ale wartość jej zmienia się bo zmienne jest napięcie i natężenie prądu. Dlatego też w przypadku prądu zmiennego do obliczenia mocy posłużymy się wartościami średnimi.
Zgodnie z naszymi obliczeniami moc w obwodzie RLC w dowolnej chwili t wynosi
|
(25.26) |
Korzystając ze wzoru na sinus różnicy kątów otrzymujemy
|
(25.27) |
gdzie ponadto skorzystaliśmy z relacji 
.
Moc średnia jest więc dana wyrażeniem
|
(25.28) |
Ponieważ 
to
(wykresy sinus i cosinus są takie same, jedynie przesunięte
o π/2). Ponadto
bo funkcja sinus jest na przemian dodatnia i ujemna.
|
(25.29) |
Jak widzimy, średnia moc zależy od przesunięcia fazowego pomiędzy napięciem i prądem.
Na podstawie wzoru (25.17) i korzystając ze związków między funkcjami trygonometrycznymi tego
samego kąta można pokazać, że 
.
Uwzględniając, ponadto że U0 = ZI0
możemy przekształcić wyrażenie na moc średnią do postaci
|
(25.30) |
Przypomnijmy, że dla prądu stałego P = I2R. Z porównania tych dwóch wyrażeń dochodzimy do wniosku, że moc średnia wydzielana przy przepływie prądu zmiennego o amplitudzie I0 jest taka sama jak prądu stałego o natężeniu
|
Definicja |
|
(25.31) |
Tę wielkość nazywamy wartością skuteczną natężenia prądu zmiennego. Analogicznie definiujemy skuteczną wartość napięcia
|
Definicja |
|
(25.32) |
|
Ćwiczenie Mierniki prądu zmiennego takie jak amperomierze i woltomierze odczytują właśnie wartości skuteczne. Wartość napięcia 230 V w naszej sieci domowej to wartość skuteczna. Jaka jest wartość maksymalną tego napięcia. Sprawdź obliczenia i wynik. |
Obliczyliśmy moc średnią wydzielaną w całym obwodzie. Porównajmy ją teraz ze średnią mocą traconą na oporze R
|
(25.33) |
Widzimy, że cała moc wydziela się na oporze R, a to oznacza, że na kondensatorze i cewce nie ma strat mocy.
Ten wniosek pozostaje w zgodności z naszymi wcześniejszymi obliczeniami.
Gdy w obwodzie znajduje się tylko pojemność lub indukcyjność (nie ma oporu omowego) to przesuniecie fazowe jest równe
π/2,
a ponieważ cos(π/2) = 0,
to zgodnie z równaniem (25.29) średnia moc jest równa zeru. Jednocześnie zauważmy, że moc chwilowa
zmienia się z czasem; raz jest dodatnia (energia jest gromadzona w polu
elektrycznym kondensatora lub magnetycznym cewki), a raz ujemna
(zgromadzona moc jest oddawana do układu).
|
Ćwiczenie Dla obwodu wejściowego radioodbiornika omówionego w ćwiczeniu w paragrafie 25.3 oblicz przesunięcie fazowe i średnią moc wydzielaną w obwodzie w przypadku rezonansu (dostrojenia do częstości f1 = 101 MHz) jak i poza rezonansem (dla częstości f2 = 96 MHz). W obwodzie R = 10 Ω, L = 1 μH, a pojemność, przy której uzyskano rezonans dla częstotliwości f1, wynosi C = 2.48 pF. Sygnał wejściowy z anteny ma amplitudę 100 μV. Sprawdź obliczenia i wynik. |
Omawiane obwody, w których elementy R, L, C
stanowiły odrębne części nazywamy obwodami o elementach
skupionych 
. W
praktyce jednak mamy do czynienia z elementami, które mają złożone własności.
Przykładem może tu być cewka, która oprócz indukcyjności L
ma zawsze opór R oraz pojemność międzyzwojową C. Mamy
wtedy do czynienia z obwodami o elementach rozłożonych
.