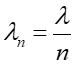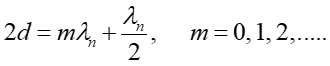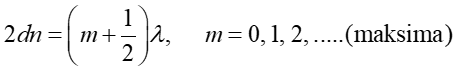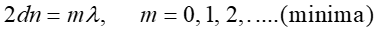Natężenie światła w doświadczeniu Younga29.4 Interferencja w cienkich warstwach
Dobrze nam znane tęczowe zabarwienie cienkich warstewek, np. baniek mydlanych czy plam oleju na wodzie jest wynikiem interferencji. Na rysunku 29.4 pokazana jest warstwa o grubości d i współczynniku załamania n.
Warstwa jest oświetlona przez rozciągłe źródło światła monochromatycznego. Dwa promienie wychodzące z punktu S źródła docierają do oka po przejściu przez punkt P. Promienie te przebiegają różne drogi gdyż jeden odbija się od górnej, a drugi od dolnej powierzchni błonki. To czy punkt P widzimy jako jasny czy ciemny zależy od wyniku interferencji fal w tym punkcie.
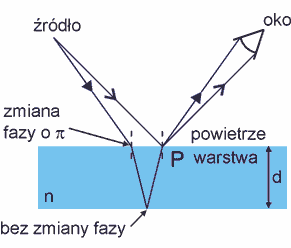
Rys. 29.4. Interferencja światła w cienkiej warstwie
Fale te są spójne, bo pochodzą z tego samego punktu źródła światła. Jeżeli światło pada prawie prostopadle to geometryczna różnica dróg pomiędzy obu promieniami wynosi z dobrym przybliżeniem 2d. Można by więc oczekiwać, że maksimum interferencyjne (punkt P jasny) wystąpi gdy odległość 2d będzie całkowitą wielokrotnością długości fali. Tymczasem wynik doświadczenia jest inny. Dzieje się tak z dwóch powodów:
- Długość fali w warstwie λn jest różna od jej długości w powietrzu λ
|
(29.25) |
Oznacza to, że musimy rozważać drogi optyczne a nie geometryczne.
- Okazuje się ponadto, że fala odbijając się od ośrodka optycznie gęstszego (o większym współczynniku załamania n) zmienia swoją fazę o π. Natomiast gdy odbicie zachodzi od powierzchni ośrodka rzadszego optycznie fala odbija się bez zmiany fazy. Oznacza to, że promień odbity od górnej powierzchni błonki zmienia fazę, a promień odbity od dolnej granicy nie.
Musimy teraz uwzględnić oba czynniki tj. różnice dróg optycznych oraz zmiany fazy przy odbiciu. Dla dwóch promieni pokazanych na rysunku 29.4 warunek na maksimum ma więc postać
|
(29.26) |
Czynnik λn /2 opisuje zmianę fazy przy odbiciu (od górnej powierzchni) bo zmiana fazy o 180° (π) jest równoważna, zgodnie z równaniem (29.21), różnicy dróg równej połowie długości fali. Ponieważ λn = λ/n otrzymujemy ostatecznie
|
(29.27) |
Analogiczny warunek na minimum ma postać
|
(29.28) |
|
Ćwiczenie Rozpatrzmy teraz bańkę mydlaną (n = 1.33) o grubości 320 nm znajdująca się w powietrzu. Powiedz, jaki kolor ma światło odbite, gdy bańka jest oświetlona światłem białym padającym prostopadle do jej powierzchni? W tym celu sprawdź dla jakiej długości fali z zakresu widzialnego (400 - 700 nm) spełniony jest warunek maksimum interferencyjnego. Sprawdź obliczenia i wynik. |
