Wstęp

30.1 Wstęp

W doświadczeniu Younga i doświadczeniu z siatką dyfrakcyjną mamy do czynienia z interferencją fal ugiętych na dwóch i wielu szczelinach (przeszkodach). Doświadczenia te stanowią więc dowód nie tylko interferencji, ale także dyfrakcji czyli ugięcia światła .

O zjawisku ugięcia promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny) mówiliśmy już w poprzednim rozdziale podając jakościowe wyjaśnienie tego zjawiska w oparciu o zasadę Huygensa.

Na rysunku 30.1a pokazano na czym polega dyfrakcja. Fala ze źródła S przechodzi przez otwór w przesłonie i pada na ekran. Natężenie w punkcie P na ekranie można obliczyć dodając do siebie wszystkie zaburzenia falowe (wektory pola elektrycznego E) docierające z różnych punktów szczeliny. Nie jest to łatwe bo te elementarne fale mają różne amplitudy i fazy. Wynika to z tego że:

Elementarne źródła Huygensa (punkty w szczelinie) są w różnych odległościach od punktu P na ekranie.

Światło opuszcza te punkty pod różnymi kątami.

Taka sytuacja, gdy fale opuszczające otwór nie są płaskie, (promienie nie są równoległe) pojawia się gdy źródło fal i ekran, na którym powstaje obraz znajdują się w skończonej odległości od przesłony ze szczeliną. Taki przypadek nosi nazwę dyfrakcji Fresnela .

Całość upraszcza się, gdy źródło S i ekran odsuniemy na bardzo duże odległości od otworu uginającego. Ten graniczny przypadek nazywamy dyfrakcją Fraunhofera . Czoła fal padających jak i ugiętych są płaszczyznami (promienie są równoległe) tak jak na rysunku 30.1b.

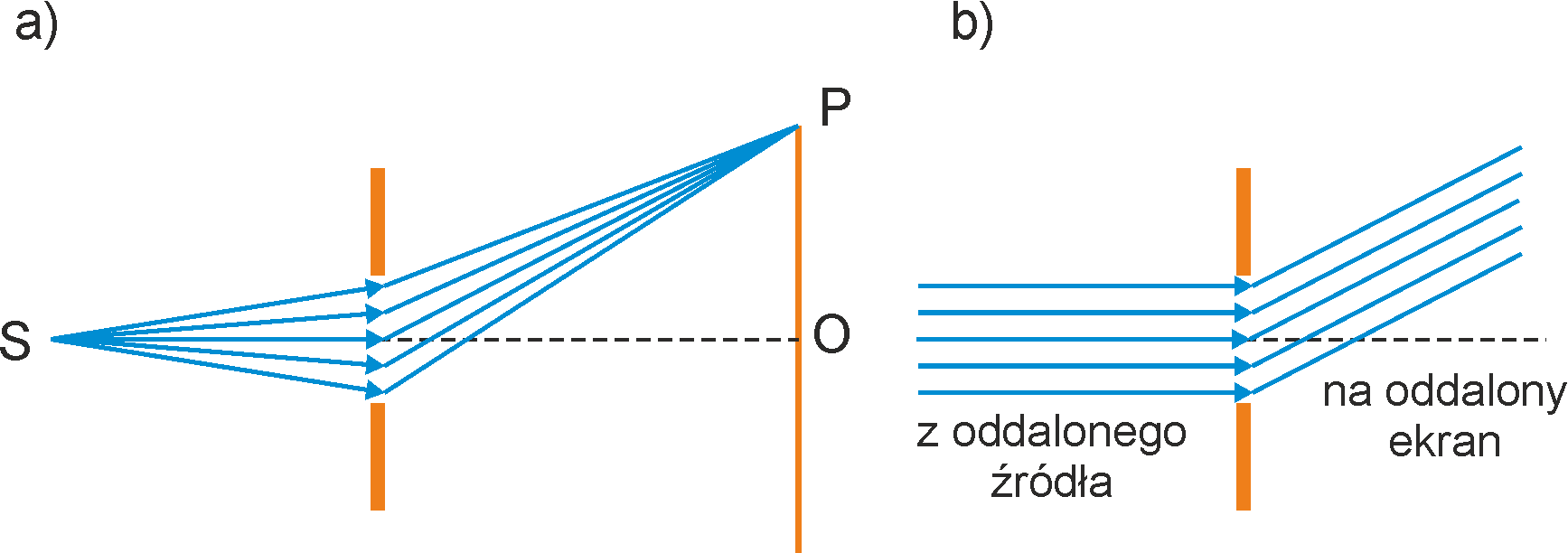
Rys. 30.1. Dyfrakcja Fresnela (a) i dyfrakcja Fraunhofera (b)

Dyfrakcję Fraunhofera można zrealizować w laboratorium za pomocą dwu soczewek skupiających. Pierwsza soczewka zmienia falę rozbieżną w równoległą, a druga skupia, w punkcie P, fale płaskie opuszczające otwór w przesłonie. W dalszej części będziemy zajmować się tylko dyfrakcją Fraunhofera.