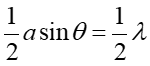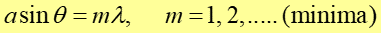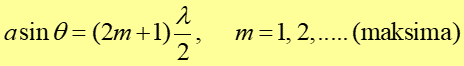30. Dyfrakcja
• Spis treści  
• Natężenie światła w obrazie dyfrakcyjnym  
•   Dyfrakcja - Wstęp

30.2 Dyfrakcja na pojedynczej szczelinie

  Rozpatrzmy falę płaską padającą prostopadle na szczelinę tak jak na rysunku 30.2. Zacznijmy od najprostszego przypadku tj. rozpatrzenia punktu środkowego O na ekranie. W tym punkcie są skupiane przez soczewkę S równoległe promienie wychodzące ze szczeliny. Te równoległe promienie przebywają do tego punktu te same drogi optyczne (choć różne geometryczne) tzn. promienie zawierają tę samą ilość długości fal. Ponieważ w szczelinie promienie są zgodne w fazie to po przebyciu takich samych dróg optycznych nadal pozostają zgodne w fazie. Dlatego w środkowym punkcie O będziemy obserwować maksimum.

Rozpatrzmy teraz inny punkt P na ekranie pokazany na rysunku 30.2. Promienie docierające do P wychodzą ze szczeliny o szerokości a pod kątem θ. Jeden promień ma początek u góry szczeliny, a drugi w jej środku. Dodatkowo pokazany jest (linią przerywaną) promień przechodzący przez środek soczewki. Promień ten nie jest odchylany i dlatego określa kąt θ.

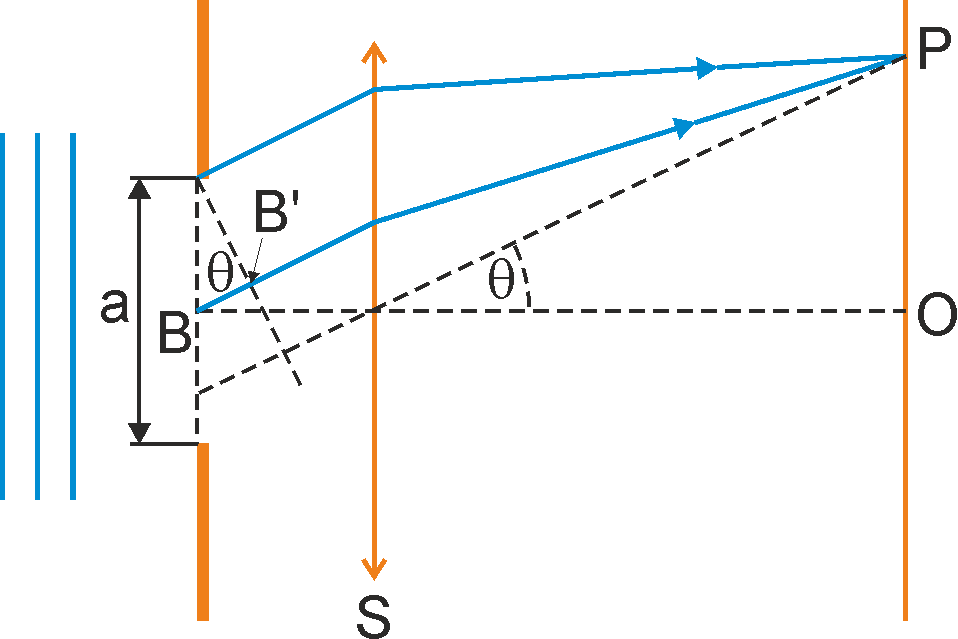
 Rys. 30.2. Powstawanie obrazu dyfrakcyjnego (dyfrakcja Fraunhofera)

Jeżeli wybierzemy punkt P tak, żeby różnica dróg BB' wynosiła λ/2 to promienie, które mają zgodne fazy w szczelinie będą miały w punkcie P fazy przeciwne i wygaszą się. Podobnie każdy inny promień wychodzący z górnej połowy szczeliny będzie się wygaszał z odpowiednim promieniem z dolnej połówki leżącym w odległości a/2 poniżej.
Punkt P będzie miał natężenie zerowe (pierwsze minimum dyfrakcyjne). Warunek opisujący to minimum ma następującą postać

Zauważmy, że gdyby szerokość szczeliny była równa λ wtedy pierwsze minimum pojawiłoby się dla θ = 90° czyli środkowe maksimum wypełniłoby cały ekran.

Podobne rozważania możemy powtórzyć dla wielu punktów szczeliny i otrzymamy ogólne wyrażenie dla minimów obrazu dyfrakcyjnego w postaci

Mniej więcej w połowie między każdą para sąsiednich minimów występują oczywiście maksima natężenia określone przez warunek