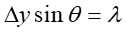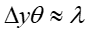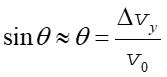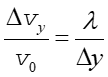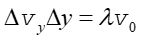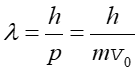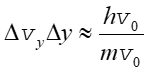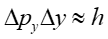Zasada nieoznaczoności

Zasada nieoznaczoności w pomiarach

Aby przetestować nasze możliwości pomiarowe rozważmy wiązkę elektronów padających z prędkością v₀ na szczelinę o szerokości Δy, tak jak na rysunku poniżej.

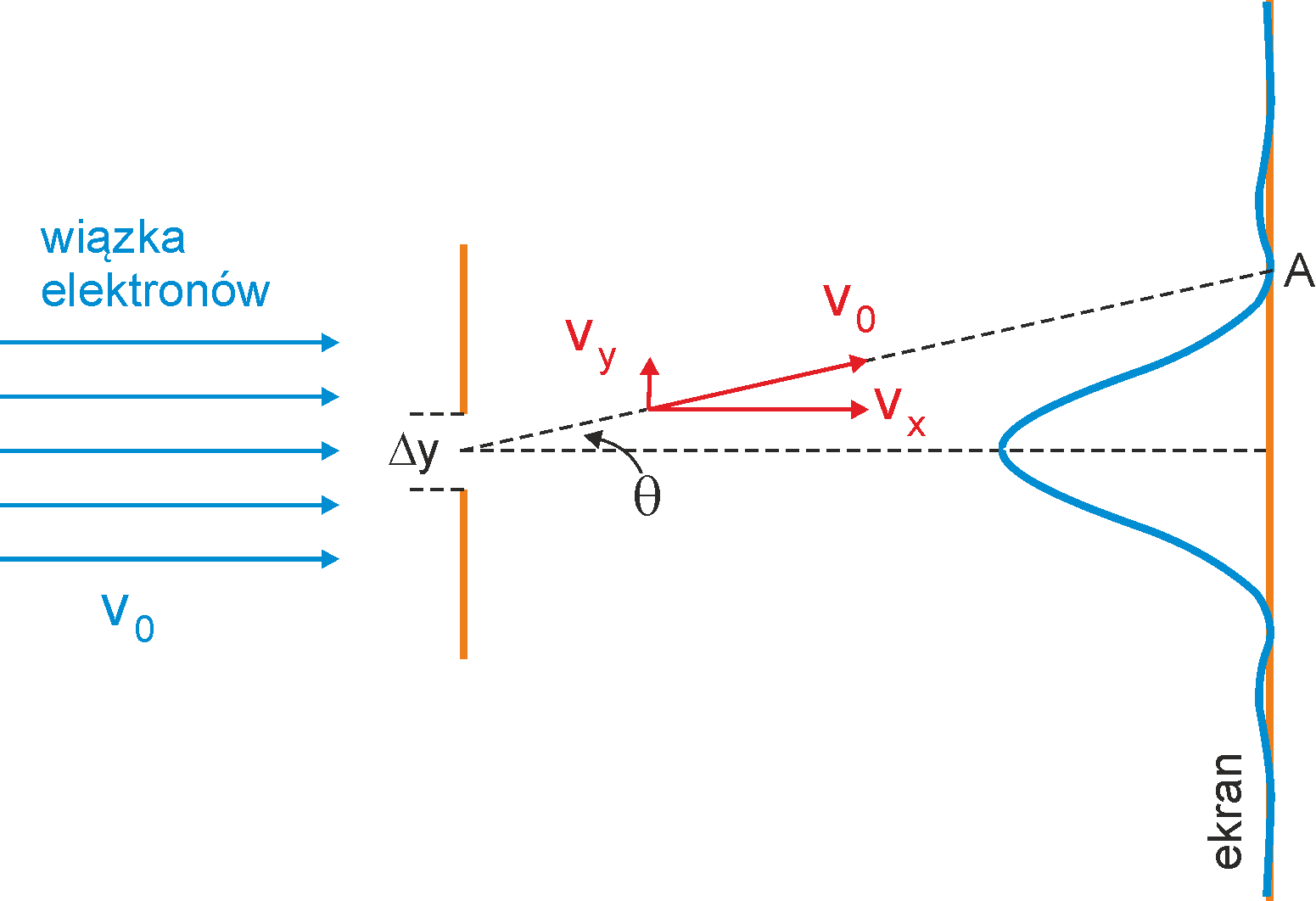
Rys. 1. Wiązka elektronów ugięta na szczelinie tworzy obraz dyfrakcyjny na ekranie

Jeżeli elektron przechodzi przez szczelinę to znamy jego położenie z dokładnością Δy. Elektrony ulegają ugięciu na szczelinie tak, że na ekranie obserwujemy obraz dyfrakcyjny. Oznacza to, że elektrony mają teraz oprócz prędkości poziomej także składową w kierunku y (są odchylone). Spróbujmy ocenić tę składową pionową prędkości.

Rozpatrzmy elektron padający na ekran w miejscu pierwszego minimum dyfrakcyjnego (punkt a na rysunku poniżej). Pierwsze minimum jest dane równaniem

(1)

a dla małego kąta θ

(2)

Elektron dolatujący do punktu a (1-sze minimum) ma prędkość pionową Δv_y taką, że

(3)

Korzystając z obu powyższych równań otrzymujemy

(4)

lub

(5)

Długość fali wiązki elektronowej jest dana przez relację de Broglie'a

(6)

Podstawiając tę zależność do równania (5) otrzymujemy

(7)

co można zapisać

(8)

Jeżeli chcemy poprawić pomiar położenia y (zmniejszyć Δy) to w wyniku zmniejszenia szerokości szczeliny otrzymujemy szersze widmo dyfrakcyjne (mocniejsze ugięcie). Inaczej mówiąc zwiększone zostało Δp_y.

Otrzymany wynik zgadza się z granicą wyznaczaną przez zasadę nieoznaczoności.

Zasada nieoznaczoności i fale materii

Według hipotezy de Broglie'a dualizmu korpuskularno-falowego każdy obiekt materialny może być opisywany na dwa sposoby: jako zbiór cząstek albo jako fala.

Dla klasycznej, makroskopowej cząstki długość fali de Broglie’a, w porównaniu z jej rozmiarami jest praktycznie równa zeru więc doświadczenia prowadzone na takim obiekcie nie pozwalają na rozstrzygnięcie czy materia wykazuje własności falowe i możemy jednoznacznie, z dowolną dokładnością określić jej położenie (patrz przykład omówiony w punkcie 34.1).

Natomiast, cząstka kwantowa, taka jak np. elektron, jest reprezentowana przez falę materii, której amplituda określa prawdopodobieństwo znalezienia cząstki. Z większym prawdopodobieństwem znajdziemy cząstkę, tam gdzie amplituda fali materii jest duża, i z mniejszym prawdopodobieństwem znajdziemy ją tam gdzie ta amplituda jest mała. Jednak fala, zajmuje pewien obszar w przestrzeni, nie jest punktowa, i dlatego położenie cząstki reprezentowanej przez tę falę, nie jest jednoznacznie określone. Pomiar położenia cząstki może dać w wyniku każdy punkt, w którym amplituda fali jest niezerowa.

Fala materii opisująca cząstkę nie rozciąga się na całą przestrzeń, ale jest skupiona w pewnym ograniczonym obszarze. Taka fala nosi nazwę paczki falowej i może być traktowana jako złożenie fal harmonicznych o różnych częstotliwościach. W przeciwieństwie do pojedynczego nieskończonego (niezlokalizowanego) ciągu falowego, nałożenie na siebie takich nieskończonych fal o długościach (częstotliwościach) należących do pewnego przedziału, daje w wyniki interferencji skończony obiekt zlokalizowany - paczkę falową (rysunek poniżej). W szczególności, sumując nieskończoną liczbę fal o częstościach bliskich sobie i amplitudach opisanych funkcją Gaussa otrzymujemy pojedynczą paczkę falową.

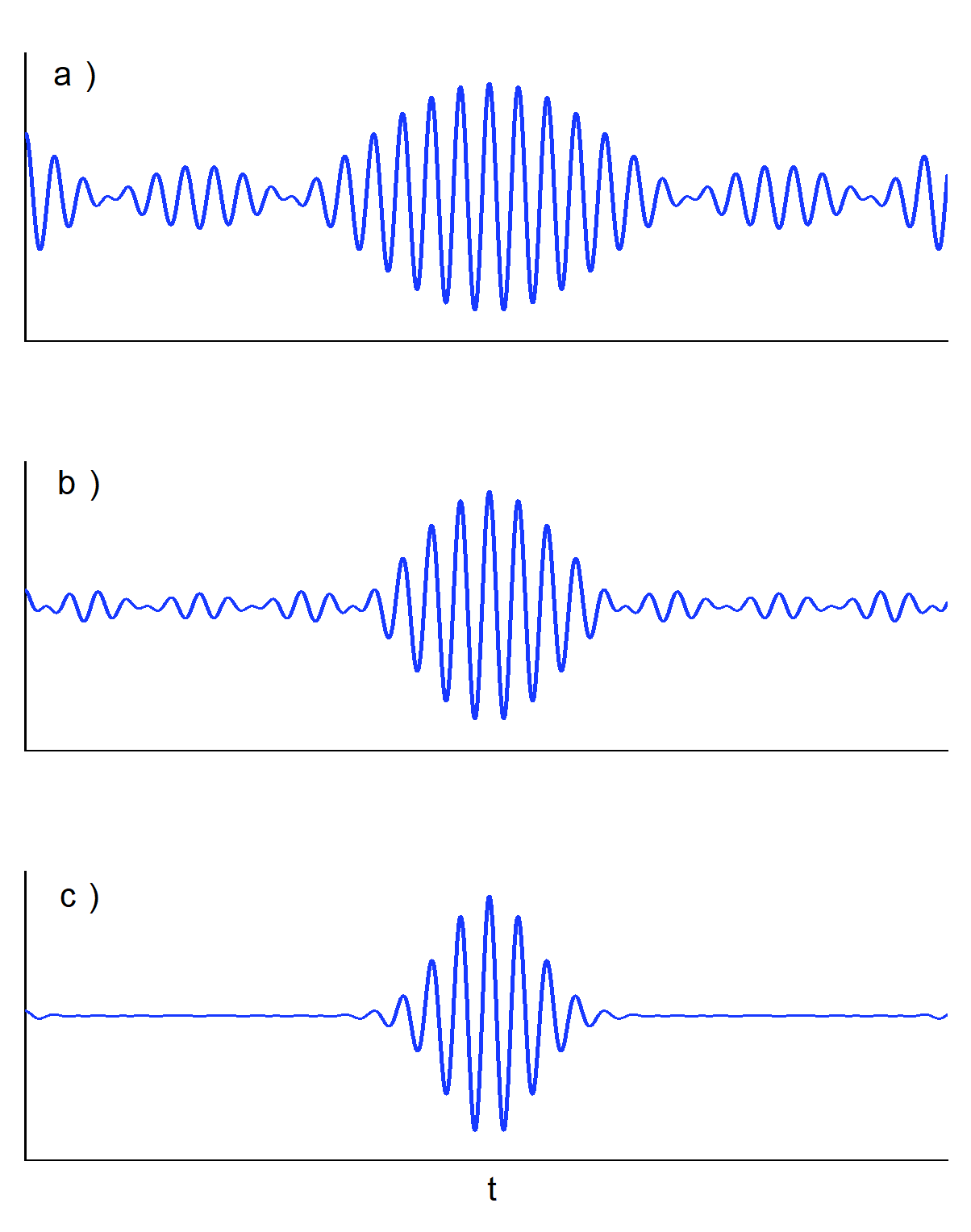
Rys. 2. Paczki falowe powstałe w wyniku złożenia odpowiednio a) 3, b) 5 i c) 11 fal o niewiele różniących się częstotliwościach

Paczka falowa, reprezentuje cząstkę zlokalizowaną uwzględniając jej falowe własności.

Ponieważ prawdopodobieństwo znalezienia cząstki jest skończone (niezerowe) w całym obszarze paczki falowej to nie mamy pewności co do jej położenia (paczka fal jest rozciągła).

Nie mamy również pewności co do pędu bo paczka falowa to złożenie fal o różnej długości czyli o różnych pędach zgodnie z relacją de Broglie’a p = h/λ. Te niepewności są „zależne od siebie”:

więcej fal tworzących paczkę to lepsza lokalizacja cząstki ale większa niepewność określenia pędu,

mniej fal tworzących paczkę to lepsza znajomość pędu, ale większe rozmycie paczki co oznacza większą niepewność określenia położenia cząstki.

Okazuje się, że nie jest możliwy jednoczesny dokładny pomiar położenia cząstki i jej pędu.

Zasada nieoznaczoności jest konsekwencją dualizmu korpuskularno-falowego.