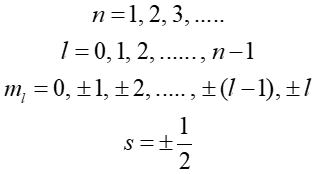Orbitalny moment pędu i spin elektronu36.2 Zasada Pauliego
W 1869 r. Mendelejew jako pierwszy zauważył, że większość własności
pierwiastków chemicznych jest okresową funkcją liczby
atomowej Z 
określającej liczbę elektronów w atomie, co najlepiej uwidacznia się
w odpowiednio skonstruowanym układzie okresowym pierwiastków. Właściwości
chemiczne i fizyczne pierwiastków powtarzają się jeżeli zebrać je w grupy zawierające 2, 8, 8, 18, 18, 32 elementów.
W 1925 r. Pauli podał prostą zasadę (nazywaną zakazem
Pauliego ), dzięki której automatycznie są
generowane grupy o liczebności 2, 8, 18, 32. Pauli zapostulował, że
|
Prawo, zasada, twierdzenie | W atomie wieloelektronowym w tym samym stanie kwantowym, może znajdować się co najwyżej jeden elektron. |
Ponieważ stan kwantowy charakteryzuje zespół czterech liczb kwantowych
|
(36.3) |
więc zasada Pauliego może być sformułowana następująco
|
Prawo, zasada, twierdzenie | W atomie wieloelektronowym elektrony muszą się różnić przynajmniej jedną liczbą kwantową. |
Przykład
Zgodnie z tą zasada na orbicie pierwszej n = 1 mogą znajdować się tylko dwa elektrony bo dla n = 1 odpowiednie liczby kwantowe zgodnie z warunkami (36.3) wynoszą
(n, l, ml, s)= (1,0,0,± ½)
Konsekwentnie, dla n = 2 mamy
(n, l, ml, s)= (2,0,0,± ½)
oraz
(2,1,1,± ½), (2,1,0,± ½), (2,1,-1,± ½)
Stąd wynika, że w stanie n = 2 może być 8 elektronów.
|
Ćwiczenie Spróbuj teraz pokazać, że w stanie n = 3 może znajdować się 18 elektronów. Zapisz liczby kwantowe odpowiadające tym orbitalom. Sprawdź obliczenia i wynik. |
Na zakończenie warto dodać, że na podstawie danych doświadczalnych stwierdzono, że zasada (zakaz) Pauliego obowiązuje dla każdego układu zawierającego elektrony, nie tylko dla elektronów w atomach.