MATLAB - Laboratorium 3.

3.1. Programy z podwójną pętlą

a) Napisz program generujący taką macierz A jak poniżej.
Jeśli wcześniej przestudiowałeś w domu OBJAŚNIENIA, to zrobisz to z łatwością. Dodatkowo zastosuj funkcję bar3(A) aby otrzymać odpowiadający macierzy A wykres słupkowy. 
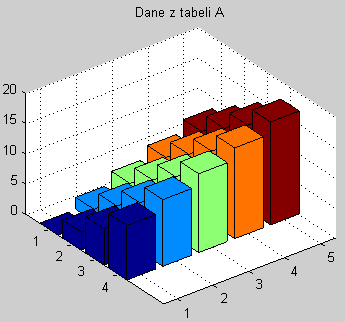
     0    2    4     6     8
     3    5    7     9    11
     6    8   10    12    14
     9   11   13    15    17

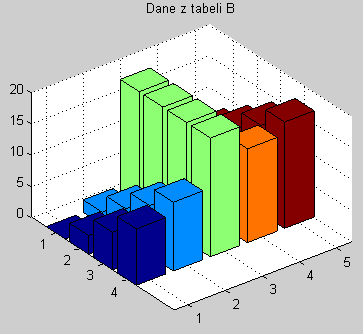
b) Zmodyfikuj program tak aby środkowa kolumna miała wartośći 19 i wyświetl jako tabelę B:
     0    2   19     6     8
     3    5   19     9    11
     6    8   19    12    14
     9   11   19    15    17

3.2. Wykresy 3D

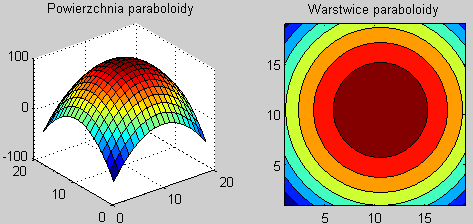
Oto wykres paraboloidy uzyskany z użyciem pętli. a) Przekopiuj i uruchom poniższy program. Zauważ, że podziałki na osiach x, y pierwszego wykresu są nieprawidłowe.
b) Zmodyfikuj program stosując tak jak w OBJAŚNIENIACH, funkcję meshgrid aby uzyskać lepszy wykres paraboloidy. 

% Paraboloida
clear; clc
Xp=-9; Xk=9; N=19
Dx=(Xk-Xp)/N; 
Yp=Xp; Yk=Xk; Dy=Dx;
y=Yp
for w=1:N
    x=Xp
    for k=1:N
        Z(w,k)=100-x^2-y^2;
        x=x+Dx
    end
    y=y+Dy
end
subplot(1,2,1); surf(Z); title('Pow...')
subplot(1,2,2); contourf(Z); title('War..')

Podpowiedź: w pętlach zmienne x,y są skalarami natomiast bez pętli zastosujemy x, y jako macierze, a mnożenia i potęgowania muszą być wtedy dokonywane na elementach a nie jako macierzowe. Pamiętasz co to są działania z kropką?

3.3. Funkcje użytkownika

Objaśnienia masz TUTAJ
a) Napisz funkcję obliczającą (z twierdzenia Pitagorasa) długość wektora na płaszczyźnie XY gdy dane są współrzędne jego początku (xp,yp) oraz końca (xk,yk):

Zastosuj tę funkcję do obliczenia obwodu trójkąta:

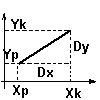
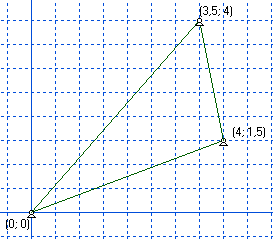
b) Napisz funkcję obliczającą odległość między dwoma punktami w przestrzeni 3D.

3.4. Ciągi, wektory, macierze i niektóre działania na nich. Rozwiązywanie układu równań liniowych

Objaśnienia masz TUTAJ
  1. Rozwiąż w Matlabie układ równań liniowych - metodą odwracania macierzy - mając daną macierz współczynników M oraz wektor wyrazów wolnych C:
    (3kb)
  2. Rozwiąż to samo zadanie metodą dzielenia lewostronnego

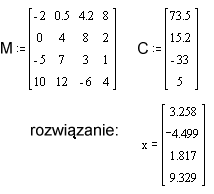
    Dodatkowo wpisz odpowiednie komendy aby otrzymać:

  3. macierz transponowaną wzgledem macierzy M oraz C
  4. wyznacznik macierzy M używając funkcji det(macierz kwadratowa)
  5. pierwszą a potem drugią kolumnę macierzy M (używając wyrażenia z dwukropkiem)
  6. element macierzy M z indeksami 1,1 oraz element z indeksami 2,2
  7. długość (liczbę elementów) wektora C - przy pomocy odpowiedniej funkcji
  8. rozmiary macierzy M oraz C - przy pomocy odpowiedniej funkcji

    9. Jak numerowane są elementy wektorów i macierzy (od 0 czy od 1)?

    Zadanie domowe 3

    Opracuj podany przez prowadzącego temat ze statyki przy użyciu obliczeń w Matlabie:

    Dany jest ciężar belki o długości 4m (lub innego elementu) oraz parametry geometryczne (wymiary, kąty) a należy z równań statyki wyznaczyć reakcje. Dla możliwości sprawdzenia poprawności uzyskanych wyników, poniższe rysunki pokazują także te szukane reakcje wyznaczone w programie symulacyjnym o nazwie Workingmodel.

    Wyznaczane reakcje (w płaskich układach sił) występują:
         a) w przegubach - wówczas trzeba wyznaczyć dwie składowe, bo kierunek nie jest znany;
         a) w punktach podparcia ślizgowego (przy założeniu braku tarcia) - wówczas kierunek reakcji jest prostopadły do powierzchni;
         a) w linkach (lub prętach) - wówczas reakcja działa wzdłuż linki.

    Przed układaniem równań trzeba określić niewiadome i zaznaczyć je na rysunku, rysując wszystkie wektory sił, a w szczególności dowolnie przyjmując wektory szukanych reakcji.

    Następnie musimy ułożyć tyle niezależnych równań ile wprowadziliśmy niewiadomych, przy czym, dla wydzielonego elementu mechanicznego, podlegającego płaskiemu układowi sił, z praw statyki wynikają najwyżej 3 równania.

    Przykłady rozwiązań uzyskanych w Mathcadzie są tutaj i tutaj, ale twoje rozwiązanie ma być przy użyciu Matlab'a.

    Rys.S10

    Rys.S11.

    Rys.S12

    Rys.S13

    Rys.S14

    Rys.S15
    ^ Powrót do spisu