

Aby otrzymać wykres drgań harmonicznych SIN(b*alfa+fi) (opisanych tutaj), najpierw:
- wpisz na arkuszu nagłówek oraz
- przygotuj komórki dla współczynników (b fi), jak na Rys.1
Kliknij teraz komórkę z wartością współczynnika i zobacz jaka nazwa pojawi się w okienku adresu (po lewej u góry)
Okazuje się, że nazwy jedno lub dwu-literowe są niedopuszczalne bo pokrywają się z nazwami kolumn arkusza więc zostały uzupełnione symbolem "podkreślnika" czyli "_".
Warto więc też poprawić nazwy na arkuszu w objaśnieniach (C3, C4 na Rys.2) chociaż nie muszą się one pokrywać ze zdefiniowanymi nazwami zmiennych.
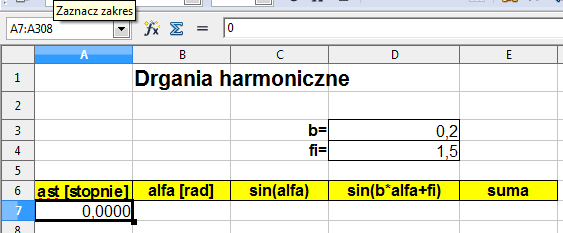 Rys.1.
Rys.1.
Chcemy teraz wygenerować automatycznie poszczególne kolumny tabelki.
|
Aby (pod nagłówkiem "ast [stopnie]") automatycznie wygenerować ciąg np.: 300 wartości kąta w stopniach (np.: od zera co 5 stopni): Zaznaczanie zakresów komórek przez wpisanie w polu adresu nad arkuszem (jak na Rys.,1) - jest prostsze i precyzyjniejsze niż przy pomocy myszki. |
Funkcje trygonometryczne wyznaczane są dla kątów podawanych w radianach
a) Pod nagłówkiem "alfa [rad]" (komórka B7) wpisz wzór przeliczający stopnie na radiany. 180 stopni to PI() radianów.
b) Następnie zaznacz zakres B7:B308 - jak poprzednio - przez wpisanie tego zakresu w polu adresu.
c) Z menu Edytuj wybierz Wypełnienie-W dół i zatwierdź.
Przypisz nazwę alfa temu ciągowi wartości kąta (w jakich on jest jednostkach?)
Można to zrobić na 3 sposoby:
(a) zaznaczyć zakres danych (już masz) i wpisać nazwę w polu adresu,
(b) zaznaczyć zakres danych (już masz) i skorzystać z menu Wstaw-Nazwy-Definiuj,
(c) zaznaczyć zakresy danych wraz z nagłówkami i skorzystać z menu Wstaw-Nazwy-Utwórz.
 Rys.2.
Rys.2.
Wpisz odpowiednie wzory pod kolejnymi nagłówkami.
Zauważ, że po wpisaniu: "=SIN(a" arkusz podpowiada: "alfa".
Uzupełnij pozostałe kolumny tabeli - wykorzystując pokazaną już operację - z menu Edytuj-Wypełnienie-W dół.
Który typ wykresy jest odpowiedni dla funkcji?. Wybranie nieodpowiedniego typu wykresu grozi błędami pokazanymi tutaj. Wstaw 3 oddzielne wykresy:
a) wykres sin(alfa) i sin(b_*alfa+fi_)
b) wykres sumy przebiegów w funkcji alfa (Rys.3) - gdy częstotliwości przebiegów niewiele się różnią, wówczas występują cykliczne zmiany amplitudy przebiegu sumarycznego (Rys.3) zwane efektem "zdudnienia":
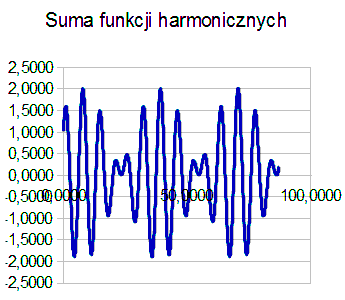 Rys.3.
Rys.3.
c) wykres krzywych Lissajous (Rys.5): na osi X sin(alfa), a na osi Y sin(b_*alfa+fi_), a więc do wykresu zaznacz tylko kolumny z tymi funkcjami.
Figury Lissaous to krzywe, w których obie współrzędne X i Y są funkcjami sinusoidalnymi zmiennej alfa lecz mogącymi różnić się częstotliwościami, ewentualnie także fazami i amplitudami. W praktyce mogą służyć do porównywania dwu sygnałów harmonicznych podawanych na wejścia X oraz Y oscyloskopu.
UWAGA: Zaznaczanie rozłącznych obszarów (kolumn) można wykonać z trzymaniem klawisza CTRL.
Klawisze strzałek z trzymaniem klawiszy Shift oraz Ctrl pozwalają natomiast zaznaczać do granic tabeli.
Ogólne objaśnienia dotyczące sporządzania wykresu masz TUTAJ.
Dla usprawnienia - częstotliwość jednego z przebiegów ma być regulowana suwakiem ("paskiem przewijania"), zmieniającym wartość współczynnika b_.
|
Pasek narzędzi FORMANTY (menu: Widok-Paski narzędzi-Formanty) pozwala wstawiać na arkusz elementy dialogowe jak: listy rozwijalne, przełączniki, przyciski, paski przewijania i in. |
|
Podpowiedzi:
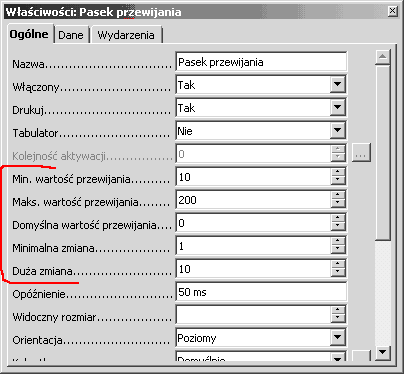 Rys.4.
Rys.4.
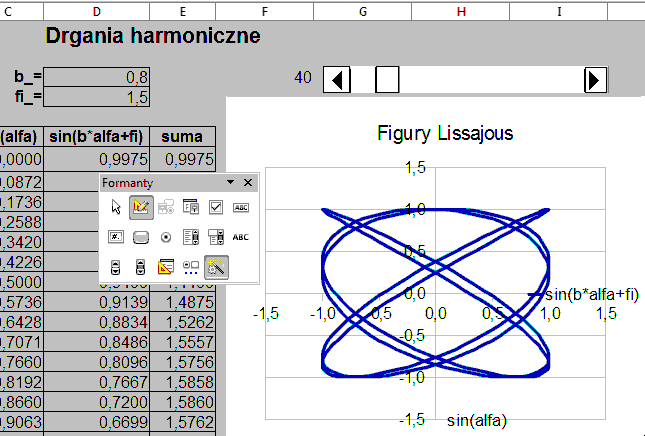 Rys.5.
Rys.5.