Objętość sześcioośmiościanu

Nie łatwo w szybki sposób wyliczyć objętość sześcioośmiościanu - jednej z brył Archimedesa. Większość osób próbowałaby dzielić tę bryłę na mniejsze części i złożyć z nich bardziej przystępną bryłę. Tak jak w przypadku poprzednich przykładów w rozwiązaniu problemu pomogą nam transformacje. Spróbujmy przekształcić nasz sześcioośmiościan w sześcian. Prezentują to poniższe rysunki i film.

Z powyższego filmu dowiedzieliśmy się, iż objętość sześcianu jest większa od objętości sześcioośmiościanu. Aby objętości obu brył były równe musimy nasz ośmiościan uzupełnić ośmiościanem dualnym do sześcianu. Ośmiościan dualny pomoże nam wyzanczyć objętość sześcioośmiościanu.

Oznaczmy literą a długość krawędzi sześcianu, natomiast literą x niech będzie długość krawędzi ośmiościanu dualnego. Liczba x jest również długością krawędzi naszego sześcioośmiościanu.

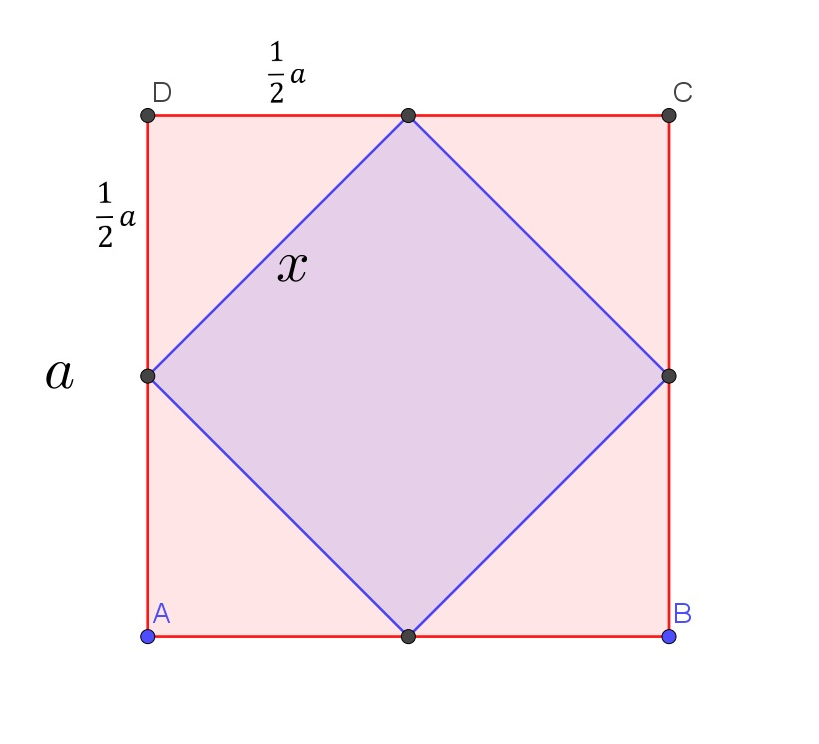
Uzależnijmy a od x. x = a√2 2 więc: a = 2x√2 2

Wyliczmy objętość ośmiościanu dualnego. Podzielmy go na dwa ostrosłupy kwadratowe. Wysokość każdego z nich jest równa a2 (połowa wysokości sześcianu). Mamy więc: V_{ośmiościanu dualnego} = 2 * V _{ostrosłupa kwadratowego} = 2 * a√2 2 * a√2 2 * a 2 * 1 3 = 2a³ 12 = 1 6 a³ 1 6 a³ = 1 6 * (2x√2)³ 8 = x³√2 3 Znając objętość ośmiościanu dualnego wystarczy odjąć ją od objętości sześcianu aby otrzymać objętość sześcioośmiościanu. V_{sześcioośmiościanu} = (2x√2)³ 8 - x³√2 3 = 48x³√2 - 8x³√2 24 = 5 3 x³√2