Jak już wiemy, w trójścianie kąty płaskie mierzy się bokami trójkąta sferycznego, na których się opierają, a kąty dwuścienne mierzy się odpowiednimi kątami trójkąta sferycznego. Związek między trójścianem, a odpowiadającym mu trójkątem sferycznym pozwala rozszerzyć twierdzenia o trójścianie na trójkąt sferyczny. W trójścianie każdy kąt płaski jest mniejszy od sumy dwóch pozostałych kątów płaskich. Te kąty płaskie mają za miarę długości boków trójkąta sferycznego, więc taka sama zależność wystepuje dla boków trójkąta sferycznego, więc:
Przenosząc jeden z wyrazów, otrzymujemy pierwszy wniosek:
a > b - c
Każdy bok trójkąta sferycznego jest większy od różnicy dwóch pozostałych boków.
Idźmy dalej. Dodając b do obu stron nierówności (a + c > b) otrzymamy (a + b + c > 2b), a dzieląc obie strony przez 2 wysuwa się nam kolejny wniosek:
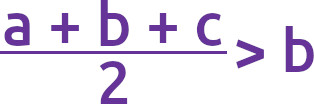
Suma kątów płaskich trójścianu jest mniejsza od 360o (α + β + γ < 360o). Zastępując w tej nierówności kąty płaskie odpowiednimi bokami trójkąta sferycznego, które są miarą tych kątów, otrzymujemy:
Suma boków trójkąta sferycznego (obwód) jest mniejsza od 360o.
Teraz skupmy się na trójkącie biegunowym. Trójkątem biegunowym względem danego trójkąta sferycznego nazywamy taki trójkąt sferyczny, dla którego boków wierzchołki danego trójkąta sferycznego są biegunami. Definicja może być nie jasna, więc spróbuję to trochę sprostować. Na początku narysujmy dowolny trójkąt sferyczny, wraz z jego trójkątem biegunowym: (WST3.1)

Przedstawmy teraz definicję trójkąta biegunowego na podstawie powyższego obrazka. Skupmy się na punkcie A. Jest on środkiem sferycznym boku EF:
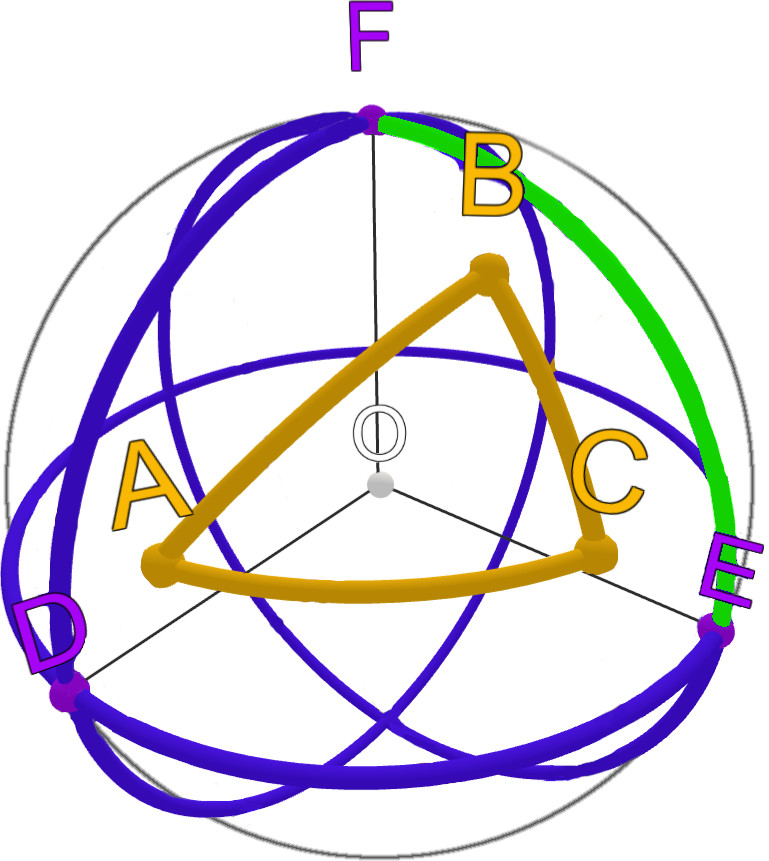
Analogicznie punkt C jest środkiem sferycznym (biegunem) boku DF:

Oraz punkt B jest środkiem sferycznym boku DE:

Wniosek z tego taki, że trójkąt sferyczny DEF jest trójkątem sferycznym biegunowym względem trójkąta sferycznego ABC. Co ciekawe, jeżeli jeden trójkąt sferyczny (DEF) jest trójkątem biegunowym względem drugiego trójkąta sferycznego (ABC), to i drugi trójkąt sferyczny (ABC) jest trójkątem biegunowym względem trójkąta pierwszego (DEF). Znaczy to tyle, iż punkt D jest środkiem sferycznym boku BC, E boku AB i F boku AC. Dla trójkątów tych prawdziwe jest twierdzenie:
Na przykład A(kąt) + EF(bok) = 180o.
Powiedzmy że mamy dwa trójkąty sferyczne ABC i DEF, biegunowe względem siebie. Zgodnie z powyższym twierdzeniem, stosując wzory: (BC = 180o - A), (AC = 180o- B), (AB = 180o- C) otrzymujemy podwójną nierówność:
Która dla danego trójkąta sferycznego wygląda tak:
Suma kątów trójkąta sferycznego jest mniejsza od 540o i większa od 180o.
Różnica między sumą kątów trójkąta sferycznego a 180o nazywana jest przewyżką/nadmiarem/ekscesem sferycznym. Przewyżka/eksces/nadmiar sferyczny jest oznaczany grecką literą ε. Wiemy już, że w trójkącie sferycznym biegunowym DEF zachodzi nierówność
DE + EF > DF. Przechodząc od trójkąta biegunowego do trójkąta ABC otrzymujemy
180o - A + 180o - B > 180o- C, więc:
W trójkącie sferycznym różnica między sumą dwóch kątów i trzecim kątem jest zawsze mniejsza od 180o.
Trójkąty sferyczne położone na powierzchni tej samej kuli są równe pod warunkiem jednakowego układu ich równych części, jeżeli mają odpowiednio równe:
1) po dwa boki i po jednym kącie zawartym między nimi
2) po jednym boku i po dwa kąty przylegające do tego boku
3) po trzy boki
4) po trzy kąty
Pierwsze trzy przypadki dowodzi się tak samo jak w równościach trójkątów płaskich w planimetrii. Dowód czwartego przypadku przeprowadza się przez zastosowanie dla danych trójkątów sferycznych ich trójkątów biegunowych. Sprawdza się, czy trójkąty biegunowe danych trójkątów sferycznych mają odpowiednie boki równe sobie. Jeżeli tak jest, to znaczy, że kąty też są sobie równe. Spójrzmy na przykład. Mamy dany trójkąt sferyczny o kątach A, B, C i bokach a, b, c oraz drugi trójkąt sferyczny o kątach D, E, F i bokach d, e, f. Załóżmy, że A=D, B=E i C=F. Naszym zadaniem jest dowieść, że tójkąty są sobie równe. Oznaczmy kąty i boki ich trójkątów sferycznych biegunowych tymi samymi literami co elementy danych trójkątów, lecz ze wskaźnikami. Wówczas z własności trójkątów biegunowych otrzymujemy następujące związki:
B + b
C + c
Ponieważ A=D, B=E i C=F, więc a
B
C
Jeżeli kąty trójkątów biegunowych są odpowienio równe, to odpowienie boki danych trójkątów też są równe, ponieważ kąty trójkątów biegunowych spełniają te boki do 180o. Z tego wynika, że dane trójkąty mają po trzy boki odpowiednio równe, a więc na podstawie trzeciego warunku równości tójkątów, trójkąty sferyczne ABD i DEF są sobie równe.
Jeżeli z wierzchołków trójkąta sferycznego ABC poprowadzimy średnice, to otrzymamy na powierzchni kuli punkty (D, E i F) przecięcia tych średnich z powierzchnią. Jeżeli otrzymane punkty połączymy łukami kół wielkich, otrzymujemy drugi, przeciwległy trójkąt sferyczny DEF, który nazywany jest symetrycznym do danego trójkąta. Jednak nie tylko takie trójkąty są zwane symetrycznymi. Będziemy tak również nazywać takie trójkąty, których wierzchołki nie leżą na końcach wspólnych srednic, lecz przez pewne przesunięcie na powierzchni kuli można je do takiego położenia doprowadzić. Logicznie myśląc wszystkie elementy trójkąta sferycznego i jego trójkąta symetrycznego są sobie odpowiednio równe. Te trójkąty nie mogą jednak do siebie przystawać (chyba że są to symetryczne trójkąty sferyczne równoramienne) z powodu innego porządku układu elementów. Tak wygląda przykład trójkąta sferycznego i trójkąta sferycznego do niego symetrycznego: (WST3.5)

Teraz przejdźmy do związków między bokami i kątami trójkąta sferycznego. Zacznijmy od pierwszego twierdzenia:
Postarajmy się to udowodnić. Weźmy pod uwagę trójkąt sferyczny ABC i załóżmy, że a = c. Naszym zadaniem jest dowieść, że kąty A i C są sobie równe. Oprócz tego połączmy wierzchołek B ze środkiem K boku AC łukiem koła wielkiego. Będzie to wyglądało tak:

Wtedy w trójkątach ABK i BKC bok BK jest bokiem wspólnym. AK jest równe KC oraz AB = BC z założenia. Trójkąty ABK i BKC mają równe boki, lecz o różnym układzie. Z tego wynika, że są symetryczne, a więc kąt A jest równy kątowi C. Teraz omówmy twierdzenie odwrotne, czyli:
Wykorzystajmy ponownie powyższą wizualizację. Mamy dane, że kąt A jest równy kątowi C. Naszym zadaniem jest dowieść, że bok a = c. Dowód przeprowadzimy z pomocą trójkąta biegunowego. Jeżeli A = C, to 180o- a
Postarajmy się udowodnić, że b > c. Narysujmy trójkąt sferyczny ABC, gdzie kąt B będzie większy od kąta C. Poprowadźmy z wierzchołka B łuk koła wielkiego tworzący z bokiem a kąt równy C. Będzie to wyglądało tak:

Z trójkąta ABK mamy: AB < AK + BK, lecz BK = KC, więc AB < AK + KC, tj. AB < AC, a więc b > c. Twierdzenie odwrotne brzmi:
Ponownie skorzystajmy z powyższego rysunku. Mamy dane, że bok b > c. Zadanie to dowieść, że B > C. Zrobimy to z pomocą trójkąta biegunowego. Jeżeli w danym trójkącie b > c, to w trójkącie biegunowym 180o- B
Źródła wiedzy:
- N. Stiepanow - Trygonometria Sferyczna (1960)
- http://www.zsi.slupsk.pl/files/uczen_zdolny/geometria.pdf
- Wykłady dr hab. Leszka Smolarka dostepne na jego stronie internetowej tutaj




