Złoty podział ma też swoje miejsce w geometrii. Istnieje wiele figur geometrycznych o boskich proporcjach, nazywanych złotymi. Zacznijmy od konstrukcji złotego odcinka i złotej liczby. Każda złota figura opiera się na tych wielkościach.

1. Trójkąt $ABC$ jest prostokątny, gdzie przyprostokątna $|BC| = 2|AB|$
2. Z twierdzenia Pitagorasa przeciwprostokątna $|CA| = \sqrt5$
3. Skonstruuj okrąg o środku w punkcie $A$ i promieniu $r =|AB|$
4. Odcinek $|AD| = |AB| = r$
5. Wyznacz Srodek $S$ odcinka $|DC|$
6. $|SC| = \frac{1 + \sqrt5}{2} = \varphi$

1. Wyznacz środek $G$ boku kwadratu $ABCD$ za pomocą prostej
2. Stwórz odcinek $GD$
3. Opuść $GD$ odcinek na przedłużenie boku $BC$
4. Stwórz nowy odcinek $CH$
5. Odcinek $BH$ jest szukanym złotym odcinkiem
(krok konstrukcji: 3-14)

Zauważ, że dzięki tej konstrukcji możemy stworzyć dwa prostokąty (krok: 14-19). Nazywamy je złotymi bo ich boki mają się do siebie w stosunku boskiej proporcji. W czerwonym prostokącie stosunek dłuższego boku $a$ do krótszego $b$ wynosi $\varphi$. Stosunek boków większego prostokąta $BHIA$ też zachowuje te proporcje: $$\frac{a+b}{a} = \frac{a}{b} = \varphi$$ Możemy udowodnić to algebraicznie. Jeśli trójkąt $GCD$ jest prostokątny, to z twierdzenia Pitagorasa: $$|GD|^2 = a^2 + (\frac{a}{2})^2 = \frac{5}{4}a^2$$ $$|GD| = \frac{\sqrt5}{2}a$$ Odkładając odcinek $GD$ na przedłużenie boku kwadratu, otrzymaliśmy dłyższy bok prostokąta $BHIA$. Jego długość to: $\frac{a}{2} + |GD|$. Krótszy bok czerwonego prostokąta $CHID$ jest równy: $$b = |GD| \;– \frac{a}{2} = \frac{\sqrt5 - 1}{2}a$$ Z tego wynika, że: $$\frac{a}{b} = \frac{2}{\sqrt5 - 1} = \frac{\sqrt5 + 1}{2} = \varphi \quad c.n.u$$

Złoty prostokąt jest ściśle powiązany z ciągiem Fibonacciego, a dokładniej mówiąc z kwadratami jego kolejnych wyrazów.

Złoty odcinek możemy skonstruować także za pomocą trójkąta równobocznego wpisanego w okrąg. Pokazał to George Odom. Dowód na to jest prosty. Skoro trójkąt jest rówbnoboczny to zachodzą równości:

$$|AF| = |EF| = |CF| = a $$ $$|DE| = |FG| = b$$ Odcinek $|EF|$ jest równy $a$ ponieważ każdy odcinek łączący środki dwóch boków trójkąta jest równoległy do trzciego boku i jest równy połowie jego długości.


Następnie z twierdzenia o dwóch cięciwach przecinającym się w jednym punkcie wynika równość:

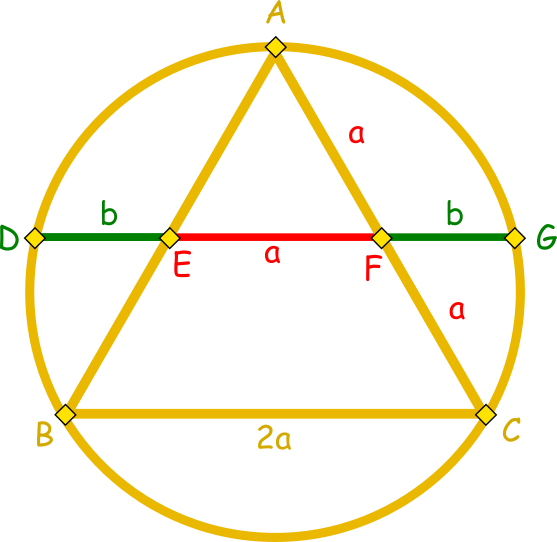
$$|AF|\cdot|FC| = |DF|\cdot|FG| $$ $$a\cdot a = (b+a)\cdot b$$ $$a^2 = b^2 + ab$$ $$\frac{a^2}{b^2} = \frac{ab}{b^2} + \frac{b^2}{b^2} $$ $$(\frac{a}{b})^2 = \frac{a}{b} + 1$$ Teraz jeśli: $x = \frac{a}{b}$ to: $$x^2 = x + 1$$ $$x^2 – x – 1 = 0$$ a to jest już znane nam równanie. Po obliczniu delty wyjdzie żę: $x = \frac{1 + \sqrt5}{2} = \varphi \quad$ c.n.u.

Trójkąt równoramienny, w którym dwusieczna kąta przy podstawie dzieli go na dwa inne trójkąty równoramienne, jest złotym trójkątem. W tym trójkącie stosunek boków wyraża się złotą liczbą, co sobie udowodnimy.

Oznaczmy kąt $\, ABD \,$ jako $\alpha$.
Wtedy: $|\sphericalangle ABD| = |\sphericalangle DBC|$,
bo $BD \;$ jest dwusieczną $\; \sphericalangle ABC$.

Skoro trójkąt $ABC$ i $DBC$
są równoramienne, to:
$|\sphericalangle BCA| = \alpha$.
$|\sphericalangle CDB| = 180^\circ - 2\alpha \;$
$|\sphericalangle BDA| = |\sphericalangle BAD| = 2\alpha$

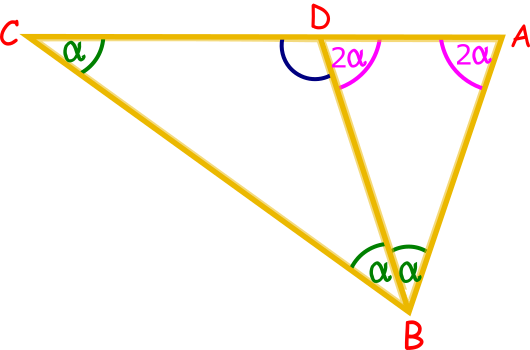
Co prowadzi do wniosku, że:
$$\bigtriangleup ABD \sim \,\bigtriangleup ABC \, (kkk)$$ Jeżeli oznaczymy $|AB|$ jako $a$ i $|DA|$ jako $b$, to z własności trójkąta równoramiennego wynika że: $|AB| = |BD| = |CD| = a$ oraz $|BC| = a + b \;$ Teraz, z wcześniej zapisanego podobieństwa: $$\frac{a}{b} = \frac{a+b}{a} = \varphi$$ A to jest nam już znany stosunek długości w złotym odcinku. Dlatego jest równy $\varphi$.

Jeżeli założymy, że $b = 1$ oraz $\, a = \varphi \;$ to $\; a + b = \varphi + 1 = \varphi^2$ (co już pokazaliśmy na pierwszej podstronie). Złoty trójkąt często opisuje się właśnie takimi długościami boków.

Z rozważań powyżej łatwo jest obliczyć wartość kątów tego trójkata:

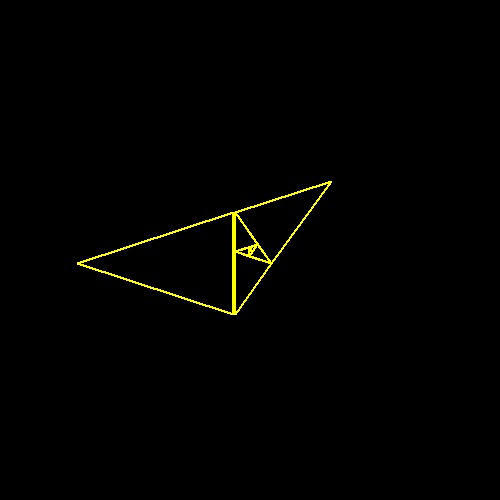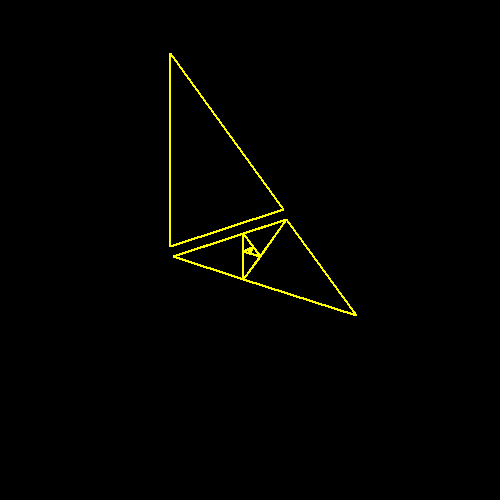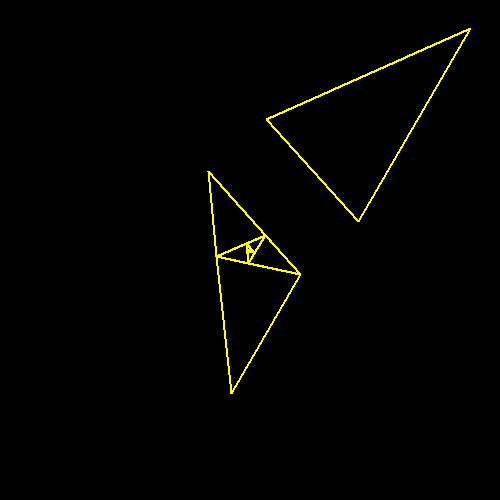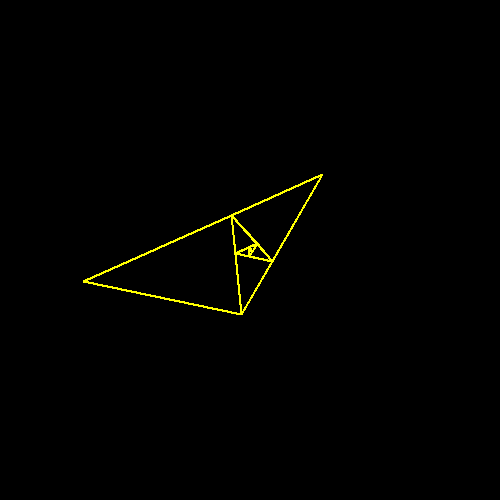
Kąty złotego trójkąta mają miarę: $36^\circ, 72^\circ, 72^\circ$. Trójkąt rozwartokątny $36^\circ, 36^\circ, 108^\circ $ często nazywa się złotym gnomonem.

W geometrii gnomon to figura która dodana do danej figury tworzy wiekszą figurę o tym samym kształcie. Zależność tą na przykładzie złotego trójkat pokazuje animacja.

Dzięki tej animacji można również dostrzeć fraktalną naturę złotego trójkąta. Jesteśmy w stanie od jego pola odejmować pole złotego gnomonu w nieskończoność, nieustannie się do niego zbliżając.

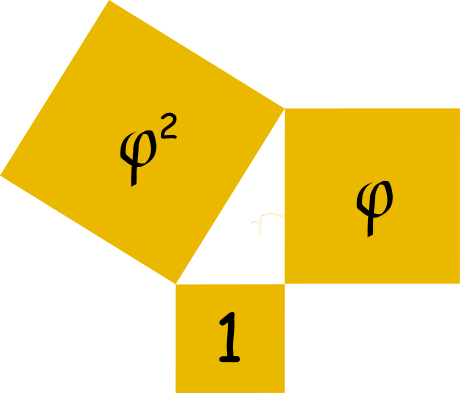
Na pewno słyszałeś kiedyś o trójkącie egipskim. Jest to trójkąt prostokątny, o stosunkach długości boków 3:4:5. Jest to jedyny trójkąt prostokątny, którego długości boków tworzą ciąg arytmetyczny. Jednak czy znasz trójkąt prostokątny ktorego boki tworzą ciąg geometryczny? Znajdzmy go!

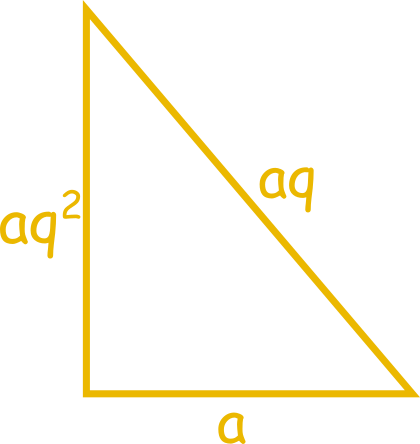
$$a^2 + b^2 = c^2$$ $$a^2 + a^2q^2 = a^2q^4 /:a^2$$ $$1 + q^2 = q^4 \qquad t = q^2$$ $$t^2 - t - 1 = 0$$ $$\Delta = 1 + 4 = 5 \qquad \sqrt\Delta = \sqrt5$$ $$t_1 = \frac{1-\sqrt5}{2} < 0 \qquad t_2 = \frac{1 + \sqrt5}{2} > 0$$ $$t_1 \neq q^2 \qquad t_2 = q^2$$ $$q = \sqrt{\frac{1 + \sqrt5}{2}} = \sqrt{\varphi}$$

Z tych działań wynika, że stosunek długości kolejnych boków takiegio trójkata musi być równy: $\; 1:\sqrt{\varphi}:\varphi$
Trójkąt o takich własnościach to trójkąt Keplera.





Jest on jedynym trójkątem prostokątnym o długościach boków w ciągu geometrycznym. Z twierdzenia Pitagorasa wynik, że suma pól kwadratów zbudowanych na przyprostokątnych tego trójkąta jest równa polu kwadratu zbudowanego na przeciwprostokątnej. Przedstawia to rysunek.

Oprócz tego możemy wyliczyć kąty tego trójkąta z własnoci trygonometrycznych. Znajdzmy kąt między bokami o długościach $\varphi$ i $1$. $$cos\alpha = \frac{1}{\varphi} = \varPhi \approx 0.61803$$ $$\alpha \approx 38.1727^\circ $$ Teraz trzeci z kątów tego trójkąta to: $$180^\circ - 90^\circ - \alpha \approx 51.8273^\circ$$

Złoty kąt to kąt środkowy oparty na mniejszym z dwóch łuków powstałych w wyniku złotego podziału okręgu. Jeżeli łuk oparty na złotym kącie oznaczymy literką $b \,$, a pozostałą część obwodu okręgu literką $\, a \,$ to cały obwód jest równy $a+b$. Wtedy zachodzi równość: $$\frac{a+b}{a} = \frac{a}{b} = \varphi$$

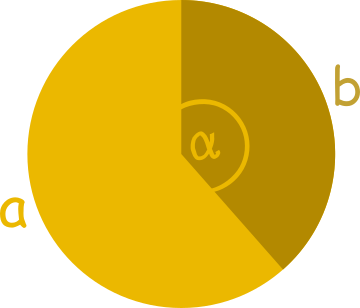
Wartość złotego kąta można prosto wyliczyć. Oznaczmy go symbolem $\alpha$. Idąc tym samym tokiem rozumowania co wcześniej, kąt oparty na łuku $\, a \,$ w stosunku do kąta $\, \alpha \,$ opartego na łuku $b \,$ jest równy $\varphi$. Kąt oparty na łuku $a \,$ jest dopełnieniem kąta $\, \alpha \,$ do kąta pełnego. Czyli:

$$\frac{360^{\circ} - \alpha}{\alpha} = \varphi \quad |\cdot \alpha$$ $$360^{\circ} - \alpha = \varphi \cdot \alpha$$ $$360^{\circ} = \varphi \cdot \alpha + \alpha$$ $$360^{\circ} = \alpha(\varphi + 1)$$ $$\frac{360^{\circ}}{\varphi + 1} = \alpha$$ jak już wcześniej opisywaliśmy: $$\varphi + 1 = \varphi^2$$ dlatego: $$\frac{360^{\circ}}{\varphi^2} = \alpha$$ $$\quad \alpha \approx 137.5^{\circ} \approx 2.399 \, \pi $$

Czyli pięciokąt foremny jest znacznie związany ze złotym podziałem. Po pierwsze stosunek jego boków i przekatnych jest równy liczbie $\varphi$. Można to udowodnić wpisując pentagon w okrąg. Przekątna $BC$ dzieli pięciokąt na trójkąt i trapez równoramienny. Jeżeli długość jego dłuższej podstawy oznaczymy literką $b$, a długość krótszej jako $a$, to długośi ramion tego trapezu też są równe $a$. Teraz z twierdzenia Ptolemeusza mówiącego, że: W dowolnym czworokącie $ABCD$ wpisanym w okrąg iloczyn długości przekątnych równy jest sumie iloczynów długości przeciwległych boków:

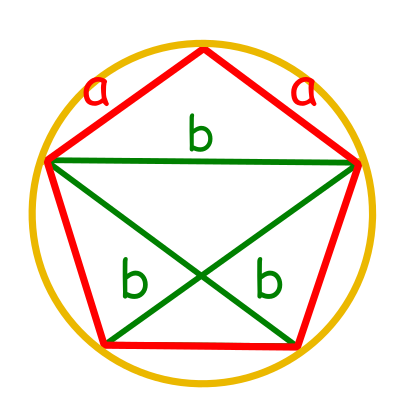
$$|AC|\cdot |BD|=|AB|\cdot |CD|+|BC|\cdot |AD|$$ $$b\cdot b = a \cdot a + b \cdot a$$ $$b^2 = a^2 + ab \; /:a^2$$ $$(\tfrac{b}{a})^2 = 1 + \tfrac{b}{a} \qquad t = \tfrac{b}{a}$$ $$t^2 - 1 - t^2 = 0 \qquad \sqrt{\Delta_t} = \sqrt5$$ $$t_1 = \varphi \qquad t_2 = \varPhi$$ $\qquad \quad$Z tego wynika że: $\tfrac{b}{a} = \varphi \;$ oraz $\; \tfrac{a}{b} = \varPhi$

Po przekształcenniu długość przekątnej b to: $$ b = \varphi a$$
Oprócz tego udowodniono, że promień okręgu opisanego na pentagonie to: $$R = \frac{a}{\sqrt{3 - \varphi}}$$ Z kolei promień okręgu wpisanego to: $$r = \frac{\varphi R}{2}$$

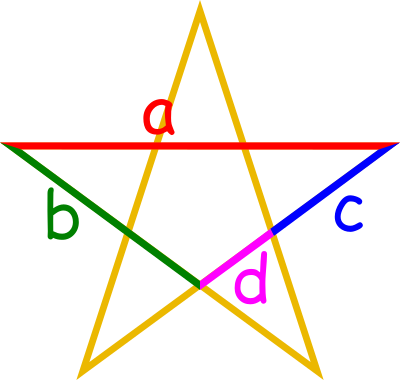
Kiedy połączymy wszystkie przekątne pięciokąta foremnego utworzy się figura przypominająca gwiazdę zwana pentagramem. Jeżeli sam pentagon miał tyle wspólnego ze złotym podziałem, to pentagram tym bardziej.

wiemy już że sama długość jego boków jest równa $\varphi$. Oprócz tego stosunek odcinków w pentagramie jest złoty: $$\frac{a}{b} = \frac{b}{c} = \frac{c}{d} = \varphi$$ Kąty ostre pentagramu mają miarę $36^\circ$ Wiedząc, że na przykład nad czerwonym odcinkiem znajduje się trójkat równoramienny, to ten trójkąt ma miary: $36^\circ, 72^\circ, 72^\circ$ czyli jest to złoty trójkąt.
Trójkąt o obwodzie zbudowanym z kolorowych odcinków ma miary kątów: $36^\circ, 36^\circ, 108^\circ$ czyli jest to złoty gnomon.

Tak więc pentagram składa się ze złotych trójkątów i złotego gnomona.

Czyli z greckiego dziesięciokąt foremny to kolejna figura foremna, w ktrórej budowie duże znaczenie ma złoty stosunek. Najłatwiej ją będzie opisać na podstawie konstrukcji poniżej.

1. Odcinek $AC$ jest złotym odcinkiem.
2. Znajdź środek odcinka $AB$ za pomocą symetralnej.
3. Skonstruuj okrąg o środku w punkcie $A$ przechodzącym przez punkt $C$.
4. Punkt $S$ przecięcia okręgu z symetralną jest jednocześnie wierzchołkiem trójkąta $ABS$.
5. Narysuj fioletowy okrąg o środku $S$ przechodzącym przez punkty $A$ i $B$. W ten okrąg wpiszemy dekagon.
6. Skonstruuj okrąg o środku w punkcie $B$ i promieniu $|AB|$.
7. Skonstruuj odcinek od $B$ do punktu przecięcia zielonego i fioletowego okręgu.
8. Powtarzaj dwa ostatnie kroki w miarę zapełniania dużego fioletowego okręgu.

Z Konstrukcji powyżej wynikają następujące fakty:
• długość boku dekagonu jest równa $|AB|$ - czerwonej części złotego odcinka,
• dziesieciokąt foremny składa się z dziesięciu złotych trójkątów,
• kąt wewnętrzny dekagonu jest równy: $\, 2 \cdot 72^\circ = 144^\circ$

Oprócz tego moża wyliczć znając własności trójkąta Keplera że:
• promień okręgu wpisanego w ten wielokąt to:
$$r = \frac{a}{2} = \sqrt{5 + 2\sqrt5}$$
• Promień okręgu opisanego na dziesięciokącie foremnym to:
$$R = \frac{a}{2}(1 = \sqrt5) = a\cdot\varphi$$
• Z tego wynika, że długość boku tej figury wynosi:
$$a = \frac{R(\sqrt5 - 1)}{2} = R\cdot\varPhi $$ Jak widać figurę tę opisuje złoty podział.

Zanim omówimy złotą spiralę określmy czym właściwie są spirale? Spirala to krzywa zakreślona przez punkt, który porusza się wokół środka spirali jednocześnie się od niego oddalając.

Spiralę najłatwiej opisać we współrzędnych biegunowych. Czyli takim układzie współrzędnych na płaszczyźnie, który jest wyznaczony przez punkt $O$ zwany biegunem oraz przez półprostą $OS$ o początku w punkcie $O$ zwaną osią biegunową. Tutaj każdemu punktowi $P$ płaszczyzny przypisujemy jego współrzędne biegunowe: $P$ $(r,\theta)$ gdzie $r$ to promień wodzący, czyli odległość $|OP|$, a $\theta$ to wartość kąta skierowanego pomiędzy półprostą $OS$, a wektorem $\overrightarrow{OP}$.

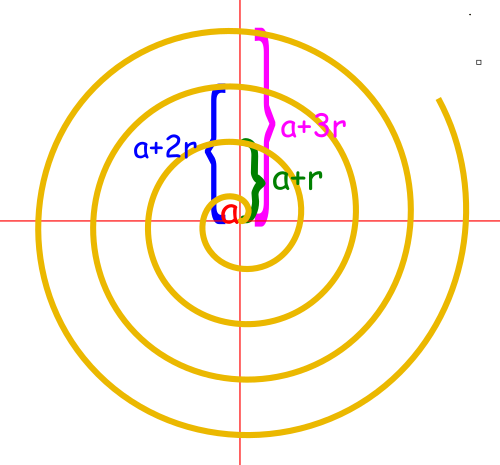
Spirale opisuje równanie: $r(\theta) = a\cdot \theta$, gdzie $a \in \mathbb{R}$. Jej najprostszym przykładem jest spirala Archimedesa. Tutaj punkt $P$ oddala się od środka oraz porusza się wokół niego ze stałą prędkością.

Jeśli ze środka spirali narysujemy półprostą, to odległości od kolejnych punktów przecięcia utworzą ciąg arytmetyczny. Gdybyśmy chcieli aby te odległości zmieniały się geometrycznie, to otrzymamy spiralę logarytmiczną. Jest to spirala dana wzorem ogólnym: $$r(\theta)= aq^n = ae^{k\theta}$$ gdzie ilorazem ciagu jest $e$. To stała matematyczna nazywana liczbą Eulera. Jest używana jako podstawa logarytmu naturalnego: $\log_e \,$. Każda półprosta wychodząca ze środka spirali logarytmicznej przecina ją pod tym samym kątem $\alpha$. $\; k \,$ we wzorze to kotangens kąta $\alpha$.

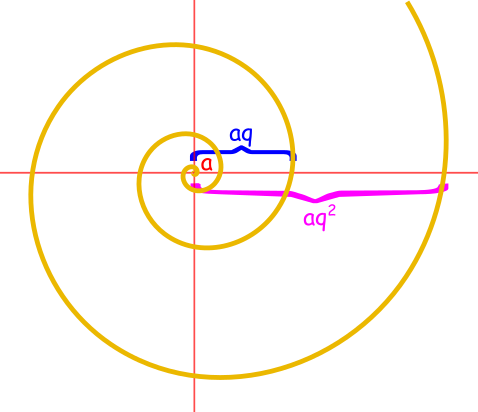
Odległości od bieguna spirali do punktów przecięcia półprostej z tą spiralą zmieniają się geometrycznie, tzn. odcinki:
$$\textsf{niebieski = czrwony} \cdot e^{2k\pi}$$ $$\textsf{różowy = niebieski} \cdot e^{2k\pi}$$

Szczególnym przypadkiem spirali logarytmicznej jest właśnie złota spirala. Jest to krzywa, w której przy zwiększeniu kąta o $90^\circ$, odległość punktu spirali od środka zmienia się $\varphi$ razy. Z tego wynika, że:

$$k= \frac{log_e\varphi}{90^\circ}\approx 0.00535$$ $$k= \frac{\log_e{\varphi}}{\frac{\pi}{2}}\approx 0,306$$ $\quad$ Tutaj także: $\quad k = ctg\alpha$, gdzie: $\quad \alpha = 73^\circ$

Określenia złota spirala i spirala Fobinacciego są czesto stosowane zamiennie. Jednak są to dwie różne spirale. Spirala Fibonacciego powstaje poprzez wpisanie do kolejnych kwadratów ćwiartek okręgów. Ona także należy do spirali logarytmicznych

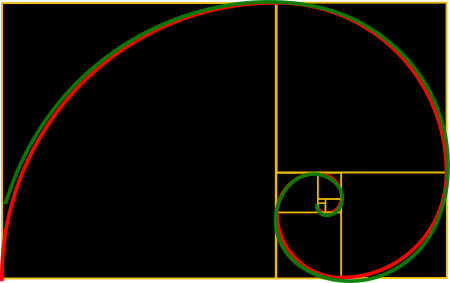
Spirala Fibonacciego jest tylko przybliżeniem złotej spirali. Mimo że są niemal identyczne nie należy ich ze sobą mylić. Grafiki powyżej przedstawia obie spirale zestawione ze sobą. Zielona to złota spirala , czerwona - spirala Fibonnaciego.

W geometrii przestrzennej wyróżniamy kilka figur związanych z boskim podziałem. Dzieje się tak, ponieważ w większości składają się one ze złotych figur, co już samo w sobie tworzy z nich "złote wielościany".

Pierwszym z nich jest dwunastościan foremny, z greckiego dodekaedr. Składa się on z dwunastu ścian w kształcie przystających pentagonów. Ma 30 krawędzi i 20 wierzchołków.

Jeśli długość jego krawędzi oznaczymy jako $a$ to:

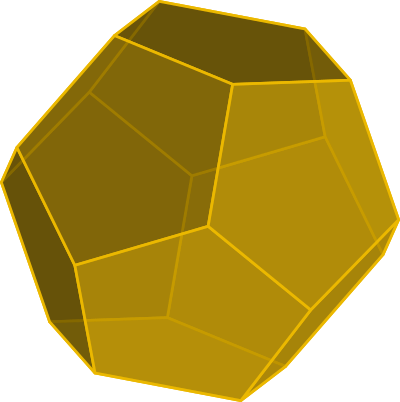
Promień $R$ kuli opisanej na wielościanie (takiej która jest styczna ze wszystkimi jego krawędziami) jest równy: $$R = a \frac{\sqrt3}{2}$$ Promień $r$ kuli wpisanej w dodekaedr (Stycznej do każdej ze ścian) wynosi: $$r=a\,{\frac {\phi ^{2}}{2{\sqrt {3-\phi }}}}$$ Pole powierzchni $P_p$ wynosi: $$P_p = \frac{15\varphi}{\sqrt{3-\varphi}}$$ Objętość $V$ to: $$V=\frac{5\varphi^3}{6-2\varphi }$$

Z greckiego ikosaedr jest wielościanem dualnym względem dwunastościanu foremnego. Ogólnie wielościanem dualnym nazywamy figurę przestrzenną skounstruowaną poprzez połączenie środków ścian figury pierwotnej.

Wielościany dualne mają następujące własności:
• wielościan skonstruowany $W_2$ ma tyle samo krawędzi co figura pierwotna $W_2$;
• wilościan $W_2$ ma tyle wierzchołków, ile $W_1$ ścian;
• Wieloscian $W_2$ ma tyle ścian, ile $W_1$ wierzchołków.

W tym przypadku jeśli odpowiednio połączymy środki pentagonów dodekaedru to otrzymamy "szkielet" dwudziestościanu foremnego. I odwrotnie, jeżeli połączymy środki ścian ikosaedru to otrzymamy konstrukcje krawędzi dodekaedru. Ab ovo Dwudziestościan foremny składa się z dwunastu trójkątów równobocznych. Ma 30 krawędzi i 12 wierzchołków. W tym przypadku jego ściana boczna nie jest złotą figurą, ale...

Jeśli długość krawędzi ikosaedru oznaczymy jako $a$ to zachodzą równości:
Promień kuli opisanej na wielościanie to: $$R = \frac{a}{2}\sqrt{\varphi \sqrt5}$$ Promień kuli wpisanej w wielościan to: $$r = \frac{\varphi^2 a}{2\sqrt3}$$ Jego pole powierzchni i objętość już nie zależy od $\varphi$Ten fakt wynika z tego, że nie składa się on już ze złotych figur. Długość jego krawędzi jest zależna od złotej liczby tylko dlatego, że jest on figurą dualną względem dodekaedru.

Z greciego triakontaedr to kolejna figura przestrzenna, której ścianami bocznymi są złote figury. Ma 32 wierzchołki i 60 krawędzi oraz składa się on z 30 złotych rombów, o których jeszcze nie wspominaliśmy.

Złoty romb to taki romb, w którym długości przekątnych są do siebie w złotym stosunku. W każdym z wierzchołków triakontaedru spotyka się trójka lub piątka złotych rombów. W dwudziestu wierzchołkach styka się kątami rozwartymi trójka, zaś w pozostałych dwunastu wierzchołkach styka się kątami ostrymi pięć rombów. W triakontaedrze kąt między dwoma przyległymi rombami wynosi $144^\circ$, czyli dwa razy więcej niż kąt między ramionami złotego trójkąta.

Jeżeli oznaczymy krawędź tego wielościanu jako $a$ to promień kuli w niego wpisanej wynosi: $$r= \frac{\varphi^2}{\sqrt{1+\varphi^2}a}$$ Na wielościanie tym nie da się opisać okręgu.

Figura ta w przeciwieństwie do dotychczasowych wielościanów nie jest foremnna. Złoty podział nie jest opisywany przez ostrosłup. To boska proporcja opisuje ten jeden konkretny przypadek.

Złotym ostrosłupem nazywamy ostrosłup prawidłowy o podstawie kwadratu, w którym apotema jest $\varphi$ razy dłuższa od połowy szerokośći podstawy. Apotema to pochylona wysokość dzieląca boczną ścianę figury przestrzennej na pół. Na rysunku jest oznaczona jako $h$. Przekrojem tej figury jest trójkąt równoramienny wyznaczony przez dwie apotemy. Połową tego trójkąta jest trójkąt Keplera. Z tego wynika, że kąt między ścianą boczną, a podstawą ma wartość około $51,8^\circ$ Oznaczmy krawędź podstawy ostrosłupa jako $a$. Jeśli przyjmiemy jak w przypadku trójkąta Keplera, że $\frac{a}{2} = 1$ to, proporcje trójkąta będącego przekrojem tego ostrosłupa są następujące: $\varphi : \varphi : 2$. Przy tym założeniu wysokość $H$ takiego ostrosłupa wynosi $\sqrt{\varphi}$.

Niektóre zródła utrzymują, że złoty ostrosłup przypomina piramidy egipskie.